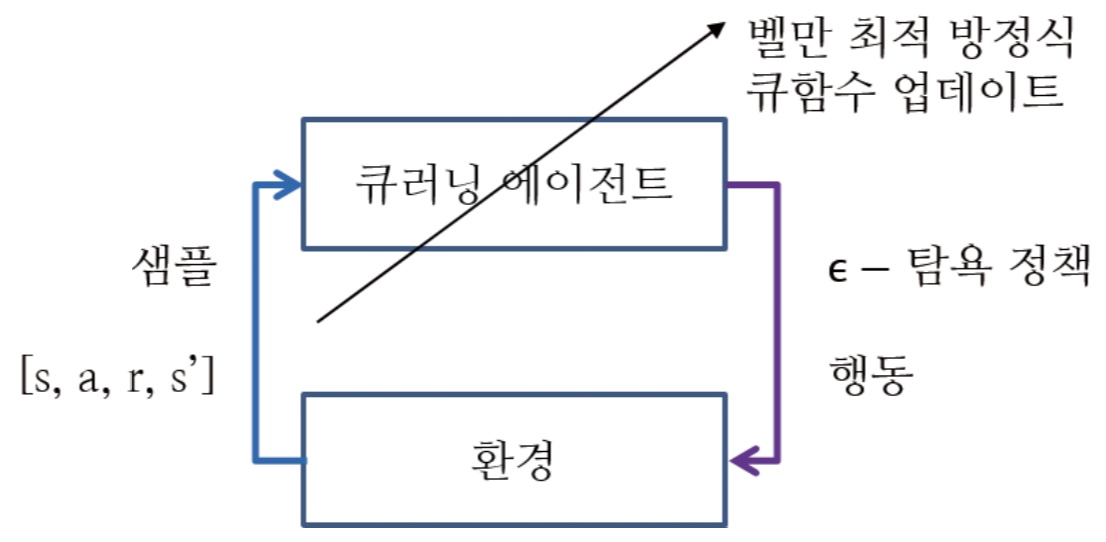
강화학습과 정책 평가 2: 시간차 예측
시간차 예측
앞에서 본 몬테카를로 예측의 큰 단점 중에 하나는 실시간이 아니라는 점이다. 가치함수가 업데이트되려면 에피소드가 끝날때까지 기다려야하는데, 에피소드의 길이가 길거나 무한할때는 몬테카를로 예측을 효율적으로 적용할 수가 없다.
이에 반해 시간차 예측은 타입스템마다 가치함수를 업데이트한다. 이전 게시물을 보면 알겠지만, 몬테카를로 예측에서 상태 반환값인 를 알기 위해서는 에피소드가 끝나야한다. 시간차 예측에서도 몬테카를로 예측처럼 샘플링을 진행하지만 그 대상이 조금 다르다
<시간차 예측에서의 가치함수의 정의>
몬테카를로 예측에서 봤던 것처럼 이런 가치함수를 시간차 예측에서 샘플링하고 업데이트 하는 과정은 다음과 같다.
<시간차 예측에서 가치함수의 업데이트>
이 식을 한번 말로 풀어서 써보자면, 매 타입스텝마다 에이전트는 현재 상태()에서 행동을 하나 선택하면 그에 대한 보상 ()을 받고, 다음 상태 ()로 이동하게 된다.
그럼 에이전트는 자신에게 있는 상태별 가치함수 리스트에서 에 해당하는 가치함수()을 가져오고, 를 계산할 수 있다. 이렇게 계산한 가 가치함수 업데이트의 목표가 된다.
- : 업데이트의 목표
- : 업데이트의 크기
를 시간차 에러라고 하는데, 재미있는 점은 시간차 예측에서 업데이트의 목표는 몬테카를로 예측에서의 반환값 것처럼 어떤 실제하는 값이 아니라는 점이다.
에이전트가 가지고 있는 다음 상태에 대한 가치함수, 가의 참 가치함수라고 예측, 가정을 해서 현재 상태의 가치함수를 업데이트 하는 방식이다. 이렇게 불확실한 업데이트 목표를 가지고 현재 상태를 업데이트 하는 방법을 부트스트랩이라고 한다.
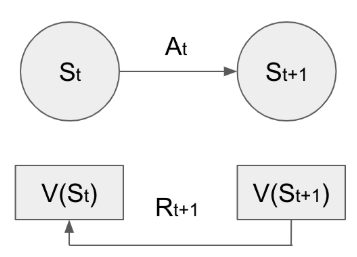
위 그림을 보면 좀 더 직관적으로 이해가 가는데, 어떤 상태에서 행동을 하면, 다음 상태로 이동하면서 그에 대한 보상을 받는다. 그러면 다음상태의 가치함수와 보상을 더한 값을 목표로 업데이트가 진행된다.
이렇게 업데이트했을 때 우리가 구하고자 하는 참 가치함수에 수렴할 수 있을까 하는 의문이 들기는 하지만, 충분히 많은 샘플링을 진행하면 몬테카를로 예측보다 훨씬 효율적으로 수렴한다고 한다. 그렇지만 처음에 가치함수 값을 어떻게 초기화 하는지에 따라서 그 정확도에 차이가 나게 된다.
강화학습 알고리즘 1: 살사(SARSA)
살사
본격적으로 얘기를 하기 전에 기초 강화학습 알고리즘의 순서도를 다시 한번 살펴보자.
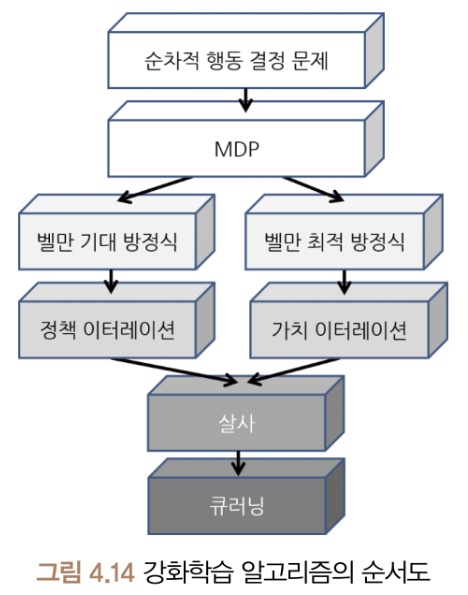
정책 이터레이션
- 정책 평가와 정책 발전을 번갈아면서 실행
- 현재 정책에 대한 정책 평가(벨만 기대 방정식) 가치함수 계산 정책 발전
정책 평가와 정책 발전을 한번씩 번갈아가면서 반복하는 정책 이터레이션을 GPI(Generalized Policy Iteration)라고 한다. GPI에서는 벨만 방정식을 계산해서 정책을 평가하지만, 앞에서 봤던 몬테카를로 예측이나 시간차 예측을 사용해서 정책을 평가할 수 있다.
생각해보면 시간차 예측은 매 타임스템마다 현재 상태에 대해서 가치함수를 업데이트하기 때문에 GPI방식 처럼 모든 상태에서의 가치함수, 모든 상태에서의 정책을 발전시킬수는 없다.
시간차 방법에서는 이런 문제를 가치 이터레이션 방법을 통해서 해결했다. 가치 이터레이션은 정책을 평가하고 발전시키는 과정 없이, 벨만 최적 방정식을 통해서 greedy하게 움직인다. 이것처럼, 시간차 예측 방법에서도 에이전트로 하여금 현재 상태에서 가장 큰 가치를 가지는 행동을 선택하는 탐욕 정책을 사용한다. 이렇게 시간차 예측과 탐욕 정책이 합쳐진 걸 시간차 제어라고 한다.
Greedy한 정책 발전을 한다는 건, 다음 상태의 가치함수를 보고 판단하는게 아니라 현재 상태에서 행동에 따른 보상만 생각하는 것인데, 이는 큐함수를 통해서 정책을 발전시키겠다는 얘기와 동일하다.
<큐함수를 통한 탐욕 정책>
큐함수에 따라서 행동을 선택하려면 에이전트는 가치함수가 아니라, 큐함수의 정보를 알아야한다는 것이고, 당연하게도 시간차 제어에서는 가치함수가 아니라 큐함수를 업데이트 해야한다는 의미이다!
<시간차 제어에서 큐함수의 업데이트>
식에서 보이다시피, 업데이트를 하기 위해서는 다음 단게에서의 큐함수 ()을 알아야한다. 즉, 다음 단계에서 어떤 행동을 선택할지를 결정해야한다. 그렇기 때문에 시간차 제어에서는 을 샘플로 사용해서 업데이트를 진행한다.
에이전트는 자신의 상태에서 탐욕 정책에 따라서 행동을 선택하고, 다음 상태로 이동하면서 그에 대한 보상을 받는다. 그리고 현재 가진 큐함수를 토대로 다음 상태에서 수행할 행동을 선택하면 하나의 샘플이 완성된다.
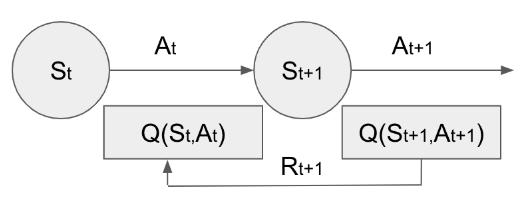
이 방식의 문제점은 학습이 덜 된 초기 에이전트는 애초에 큐함수가 잘못된 값에 수렴될 수 있기 때문에 결국 잘못된 정책을 학습하게 될 수도 있다는 점이다. 이 문제를 방지하려면 에이전트에게 충분히 다양한 경험을 하고 탐험을 할 수 있도록 해야한다.
에이전트가 더 많은 탐험을 할 수 있도록 만들어주는 새로운 정책이 -탐욕정책이다. 아이디어 자체는 되게 간단한데, 기존에는 greedy하게 가장 큰 큐함수를 선택했다면, 의 확률로 greedy한 선택이 아닌 다른 행동을 선택하도록 하는 것이다.
<-탐욕 정책>
밑에 그림처럼 기존의 GPI에서 정책 평가를 큐함수를 통한 시간차 예측으로, 정책 발전을 -탐욕 정책으로 변경한 방법이 살사라고 할 수 있다.
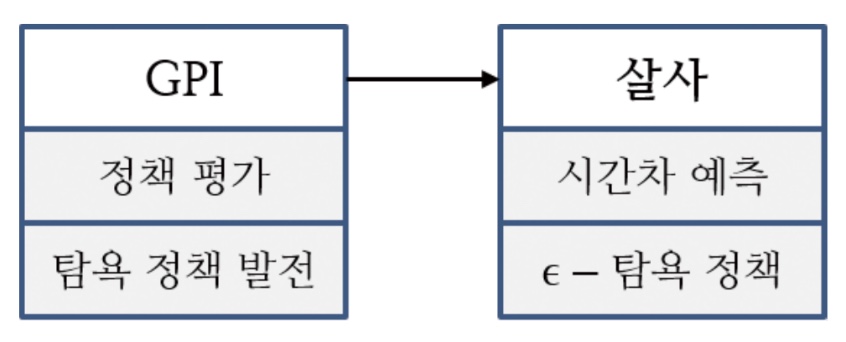
마지막으로 살사를 두 단계로 요약하면 결국
- -탐욕 정책으로 샘플 을 얻는다
- 획득한 샘플로 큐함수 를 업데이트 한다
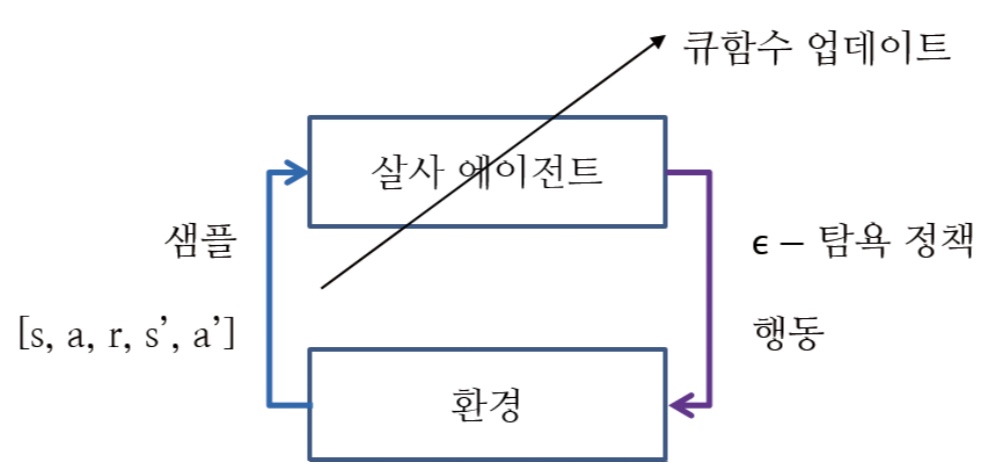
큐함수를 업데이트 하는 식은 위에서 봤던 식과 동일하다.
강화학습 알고리즘 2: 큐러닝(Q-Learning)
1. 살사의 한계
살사가 되게 잘 구성이 되어있다고 생각을 했지만, 이 방식도 문제가 있다. 살사에서는 현재 상태에서 큐함수를 업데이트 할 때에 다음 상태에서의 행동을 고려한다.
예를 들어서 지금 상태에서 큐함수에 따라서 선택한 행동은 greedy했던 반면에, 다음 상태에서 선택한 행동은 -탐욕 정책에 따라서 적은 보상을 주는 곳으로 이동했다고 생각해보자.
이렇게 모인 샘플은 현재 상태의 큐함수를 업데이트할 때에 상대적으로 낮은 값을 반환할 것이고 해당 행동에 대한 큐함수 값은 작아지는 방향으로 업데이트 될 것이다. 그 결과 해당 행동이 최적임에도 해당 행동을 학습하지 못하고 잘못된 정책을 학습할 것이다.
이 문제가 발생하는 이유는 살사가 온 폴리시 시간차 제어 (On Policy Temporal-Difference Control) 방식 즉, 자신이 행동하는 대로 학습하는 제어 방식이기 때문이다. 강화학습에서는 다양한 경험이 필요하므로 탐험의 과정이 반드시 필요하지만 이로 인해 옳바르지 않은 행동 학습하게 되는 딜레마에 빠지는 것이다.
이를 해결하기 위해 등장한 개념이 오프 폴리시 시간차 제어 Off-Policy-Temporal Difference control, 다른 말로는 큐러닝(Q-Learning)이다.
2. 큐러닝 이론
On-Policy 방식이 행동하는 대로 학습하는 것으로 미루어 보았을 때, Off-Policy 방식은 행동하는 정책과 학습하는 정책이 별개로 작동하는 방식이라고 이해할 수 있다. 즉, 에이전트는 "행동하는 정책"을 따라서 지속적으로 탐험을 하고, 이와 별개로 따로 "목표 정책"을 둬서 학습을 진행한다.
살사는 정책이 따로 존재하지는 않고, 큐함수를 토대로 greedy하게 행동을 선택하는 것이 정책이다. 그럼 큐러닝에서는 어떻게 행동 정책과 목표 정책을 별도로 구분했을까?
살사에서는 현재 상태에서 -탐욕 정책으로 행동을 선택하고, 그 다음 상태에서도 -탐욕 정책을 선택해서 업데이트에 반영한다. 반면에 Q-러닝에서는 현재 상태에서 동일하게 -탐욕 정책를 통해 행동을 선택하지만, 다음 상태에서는 가장 큰 큐함수를 업데이트에 반영한다.
즉, 다음 상태에서 실제로 어떤 행동을 했는지와는 별개로 현재 상태의 큐함수를 업데이트할 때에는 다음 상태에서의 greedy 한 행동을 토대로 진행하는 것이다. 따라서 Q러닝에서는 를 샘플로 사용한다.
<Q러닝을 통한 큐함수 업데이트>
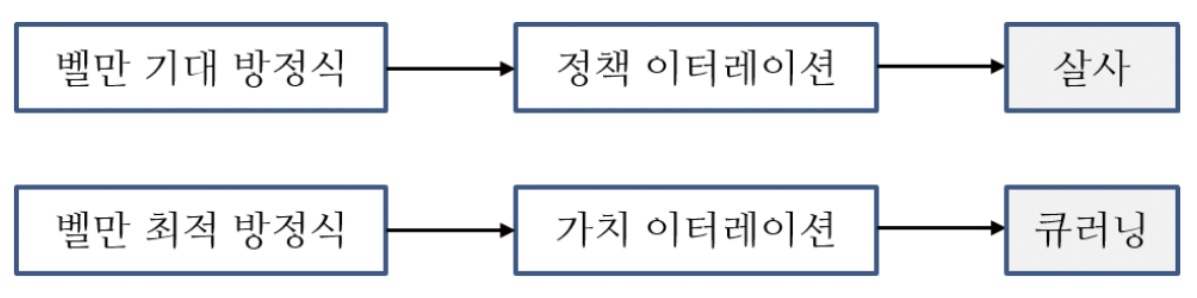
정리를 해보자면, 살사와 큐러닝 모두 -탐욕 정책으로 현재 상태에서의 다음 상태로의 행동을 선택하지만,
- 살사에서는 벨만 기대 방정식을 이용한 정책 이터레이션으로 큐함수 업데이트
- 큐러닝에서는 벨만 최적 방정식을 통한 가치 이터레이션을 기반으로 큐함수 업데이트
정리
강화학습과 정책 평가1:몬테카를로 예측
- 몬테카를로 예측은 샘플링을 통한 평균값으로 복잡한 기댓값 계산을 대체하는 기법
- 한 번의 에피소드를 진행하고, 지나온 상태들에 대한 반환값을 계산
- 계산한 반환값은 하나의 샘플이 되고, 반환값에 따라 각 상태에서의 가치함수 업데이트
강화학습과 정책 평가2:시간차 예측
- 몬테카를로 예측과 달리, 매 타임스텝마다 큐함수를 업데이트
- 벨만 기대 방정식을 사용해서 큐함수 업데이트
강화학습 알고리즘1:살사
- -탐욕 정책에서 모든 상태에 대한 가치함수를 구할 수 없으므로 큐함수 사용
- 큐함수를 사용하는 시간차 제어에서는 하나의 샘플로 를 사용
- 에이전트가 행동하는 대로 학습하는 On-Policy 방법
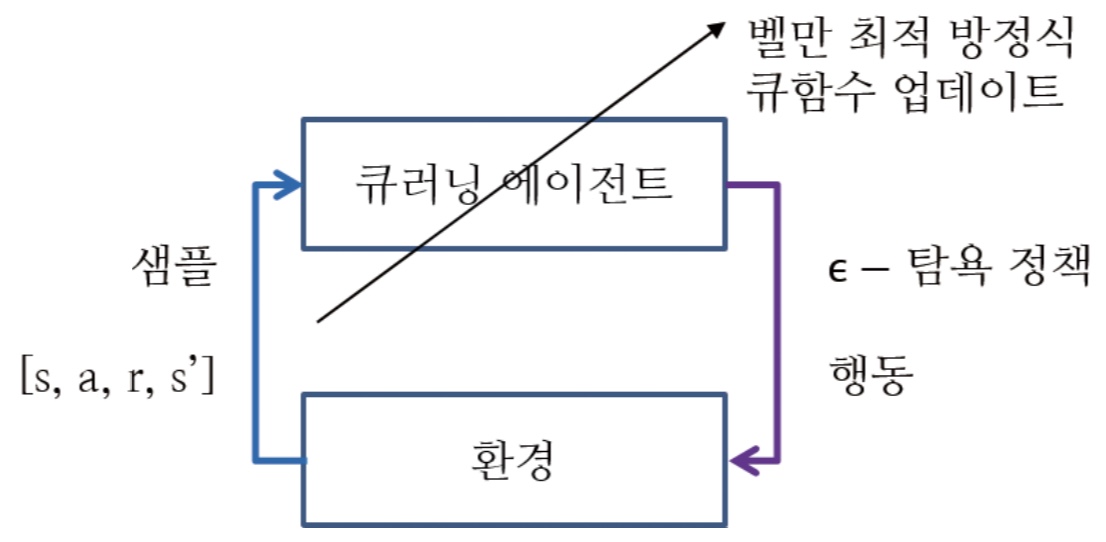
강화학습 알고리즘2:큐러닝
- On-Policy방식의 단점을 해결한 Off-Policy 방법
- 에이전트가 실제로 행동하는 정책과, 학습하는 정책을 별도로 구분
- 행동 선택 : -탐욕 정책
- 큐함수 업데이트 : 벨만 최적 방정식 (greedy)
