3장. 그리드월드와 다이내믹 프로그래밍

다이내믹 프로그래밍은 작은 문제들이 큰 문제에 중첩되어있을 때, 작은 문제의 답을 다른 작은 문제에 사용하는 것이다.
정책 이터레이션 : 벨만 기대 방정식(정책과 가치함수의 관계식)을 푸는 것
가치 이터레이션 : 벨만 최적 방정식(가치함수 사이의 관계식)을 푸는 것

다이내믹 프로그래밍과 그리드월드

1. 순차적 행동 결정 문제

2장에서 MDP를 정의하고 벨만 방정식을 세웠다. 벨만 방정식을 통해 순차적 행동 결정 문제를 푸는 방법은 다음과 같다.

• Step1. 순차적 행동 문제를 MDP로 전환
• Step2. 가치함수를 벨만 방정식으로 반복 계산
• Step3. 최적 가치함수와 최적 정책을 계산

벨만 최적 방정식을 통해 에이전트는 $v^*$를 찾는 것이 목표이다. 이 값을 찾으면 에이전트는 최적 가치함수를 알아낸 것이다.

2. 다이내믹 프로그래밍

벨만 방정식은 다이내믹 프로그래밍을 통해 해결한다. 다이내믹 프로그래밍에서는 큰 문제를 바로 푸는 것이 아니라 작은 문제들을 풀어나가면서 해결하고, 이를 통해 계산량을 줄일 수 있다.

위의 그림에서는 총 3가지 상태 ($S_1, S_2, S_3$)이 있다고 가정했다.

문제의 목표는 각 상태의 가치함수 ($v_\pi(S_1), v_\pi(S_2), v_\pi(S_3)$)를 찾는 것이다.

각 가치함수를 찾는 것이 큰 목표이고, $v_\pi(S)$를 한번에 구하는 것이 아니라 여러번에 나눠서 구하는 것이 다이내믹 프로그래밍이다.

iteration = k에서 계산을 통해 iteration = k+1에서 가치함수를 업데이트하고, 똑같은 과정을 계속해서 반복한다. 이를 통해 이전의 정보를 통해 효율적으로 업데이트 할 수 있게된다.

벨만 기대 방정식을 이용하는 다이내믹 프로그래밍 $\rightarrow$ 정책 이터레이션

벨만 최적 방정식을 이용하는 다이내믹 프로그래밍 $\rightarrow$ 가치 이터레이션

3. 격자로 이루어진 간단한 예제 : 그리드월드

앞으로의 설명을 위해 위와 같은 그리드월드를 예시로 설정했다.

빨간색 네모 : 에이전트
파란색 동그라미 : +1 보상
초록색 세모 : -1 보상
$\Rightarrow$ 파란색 동그라미에 도착해서 +1 보상을 받을 수 있는 최적 정책을 찾자!!

다이내믹 프로그래밍1 : 정책 이터레이션

1. 강화학습 알고리즘의 흐름

MDP부터 강화학습의 기본 알고리즘까지의 흐름은 다음과 같다.

MPD의 목표는 에이전트가 받을 보상의 합을 최대화 하고, 가치함수를 통해 그 목표에 얼마나 다가갔는지 평가할 수 있다. (가치함수 : 에이전트가 받을 보상의 합에 대한 기댓값)

정책 이터레이션과 가치 이터레이션을 통해 MDP를 해결한 이후 살사(SARSA)로 발전한다. 살사는 이후 오프폴리시(off-policy) 방법으로 변형되어 큐러닝(Q-Learning)으로 이어진다.

2. 정책 이터레이션

정책 이터레이션은 벨만 기대 방정식으로 정의되는 MDP를 푸는 다이내믹 프로그래밍의 방법이다.
정책은 에이전트가 어떤 상태에서 어떻게 행동할지에 대한 정보이고, MDP를 해결하여 가장 높은 보상을 얻도록 하는 정책을 얻는 것이 목표이다.

처음에는 random으로 행동을 정하는 정책에서 시작한다.

더 나은 정책으로 업데이트하기 위해서는 현재의 정책을 평가하고 더 나은 정책으로 발전해야한다. 정책 이터레이션 과정에서 "평가"는 "정책 평가"라고 하고, 발전을 "정책 발전"이라고 한다.
평가하고 발전시키는 과정을 반복해서 최적의 정책을 산출한다.

3. 정책 평가

정책을 평가하는 기준이 2장에서 배웠던 가치함수이다.
가치함수는 현재의 상태 $s$에서 정책 $\pi$를 따랐을 때 받을 수 있는 보상의 기댓값이다. 즉, 지금의 정책으로 보상을 얼마나 받을 수 있을지 알아낼 수 있다.

위의 식을 벨만 기대 방정식의 형태로 나타내면 다음과 같다. 벨만 기대 방정식 형태로 수정하면 한번에 한 타임스템의 보상만 고려하면 되기 때문에 효율적인 계산을 할 수 있다.

벨만 기대 방정식은 기댓값을 나타낸 것이고, 계산을 위해 확률적인 부분들의 합으로 나타내면 다음과 같다.

예시로 들었던 그리드 월드에서는 어떤 행동에 대해 원하는 대로 상태가 변할 확률을 1로 설정하였기 때문에($P_{ss'}^a = 1$) 다음과 같이 가정할 수 있다. 할인율 $\gamma$는 0.9로 설정했다.
Ex) 오른쪽으로 가는 행동을 하면 무조건 오른쪽으로 이동

정책 평가는 특정 정책 $\pi$에 대해 반복적으로 수행하는 것이기 때문에 계산의 단계인 변수 $k=1, 2,3,4...$를 설정해야한다. $k$번째 가치함수를 통해 $k+1$번째 가치함수를 찾는 방법은 다음과 같다.

위의 그림처럼 가치함수를 업데이트 하기 위해서는 다음 타임스텝의 상태에서 가치 함수 V를 이용해야한다. 예시에서 에이전트는 상,하,좌,우로 이동할 수 있고, 그에 따라 상태는 상,하,좌,우로 이동한다. 행동에 대한 보상 $r$과 다음 상태의 가치함수 $v_k(s')$에 할인율 $\gamma$를 고려해서 계산한다. 이러한 과정을 그리드월드의 모든 상태(좌표)에 대해서 진행하며 평가를 진행한다.

• Step1. $k$번째 가치함수의 상태 $s$에서 갈 수 있는 다음 상태 $s'$의 가치함수 $v_k(s')$를 불러온다

• Step2. 행동에 대한 보상 + 할인율*가치함수

  $r(s,a) + \gamma v_k(s')$

• Step3. 그 행동을 선택할 확률 (정책 값) 곱

  $\pi(a,s)(r(s,a) + \gamma v_k(s'))$

• Step4. 모든 선택 가능 행동에 대해 반복

  $\sum_{a \in A}\pi(a,s)(r(s,a) + \gamma v_k(s'))$

• Step5. Step4의 결과를 모두 더한 값을 $k+1$ 번째 가치함수의 $s$자리에 저장

• Step6. Step1~5를 모든 상태 $s\in S$에 대해 반복
  
  

4. 정책 발전

정책 평가 이후에는 정책을 발전시켜야한다.
여러가지 정책 발전 방법이 있지만, 해당 책에서는 탐욕 정책 발전(Greedy Policy Imporovement)를 사용한다.

정책은 모든 상태 $S$에 대해 정의되어있기 때문에 모든 상태에 대해 발전시켜야한다. 그리드 월드 예시에서 초기 정책은 특정 상태 $s$에서 무작위로 행동하는 정책으로 다음과 같다.

정책 평가를 통해 모든 상태에서의 가치함수를 구했는데, 가치함수를 통해서 어떤 행동이 좋은지는 큐함수를 통해 알 수 있다.

에이전트는 위의 식을 통해 상태 $s$에서의 $q_\pi(s,a)$를 비교해서 그 중에 가장 큰 큐함수를 가지는 행동 $a$를 선택하면 된다.

탐욕 정책 발전 방식을 통해 업데이트시킨 수식은 다음과 같다.

이런 방식으로 정책을 업데이트 하면, 업데이트 이후의 가치 함수가 무조건 크거나 같다. 따라서 장기적으로 가장 큰 기댓값을 가지는 최적 정책에 수렴할 수 있다.

다이내믹 프로그래밍2 : 가치 이터레이션

1. 명시적인 정책과 내재적인 정책

정책 이터레이션에는 명시적인 정책이 있다.
그 정책을 평가하는 도구가 가치함수이고, iteration을 반복하면서 최적 정책으로 수렴해간다. 즉, 정책과 가치함수가 명확하게 분리되어있다.

정책이 독립적이기 때문에 결정적인 정책인지, 확률적인 정책인지 상관이 없다. 대부분의 정책은 확률적인 정책이고, 이를 고려해서 가치함수를 계산하려면 당연히 기댓값을 사용해야한다. 이런 이유로 정책 이터레이션에서는 벨만 기대 방정식을 사용했다.

그런데 최적의 정책을 찾을때, 현재 가치함수가 최적이라고 가정하고 결정적인 형태의 정책만 정의되면 어떨까?(최적 정책은 결정론적임) 현재 정책이 최적이 아니더라도 어차피 iteration을 반복해서 가치함수를 발전시키면서 최적에 도달하기 때문에 굳이 확률적인 정책을 사용할 필요가 없다. 이렇게 현재 가치함수가 최적이 아니지만 최적이라고 가정하고, 결정적인 정책을 적용하여 업데이트하는 방법이 가치 이터레이션이다.

가치 이터레이션에서는 정책에 대한 얘기는 하지 않고, 가치 함수만 업데이트한다. 정책 이터레이션과 다르게 가치 이터레이션에서는 정책이 가치함수 내에 내재적으로 포함되어있다. 따라서 가치함수를 업데이트하면 자동으로 정책도 발전한다.

2. 벨만 최적 방정식과 가치 이터레이션

앞에서 봤던 벨만 기대 방정식을 통해 전체 문제를 풀어서 나오는 것은 현재 정책을 따라갔을 때 받는 보상, 가치함수이다.

1) 가치함수를 현재 정책의 가치함수라고 가정
2) 반복 계산
3) 현재 정책에 대한 참 가치함수

벨만 최적 방정식을 통해 전체 문제를 풀어서 나오는 것은 최적 가치함수이다.

1) 가치함수를 최적 정책의 가치함수라고 가정
2) 반복 계산
3) 최적 정책에 대한 참 가치함수

벨만 최적 방정식에서는 처음부터 최적 정책이라고 가정을 했기 때문에 정책 발전이 필요 없고, 정책 평가만 하면 최적 가치함수와 최적 정책이 구해진다.

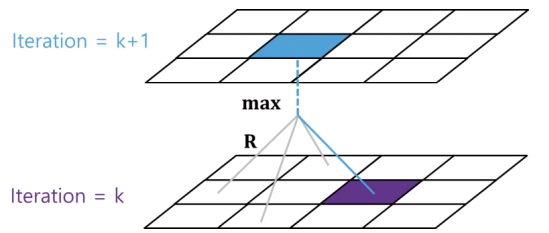
벨만 기대 방정식에서는 $E_\pi$에 정책 $\pi$가 포함되기 때문에 정책의 값을 고려해줘야한다. 반면에 벨만 최적 방정식에서는 현재 상태(최적)에서 가능한 $R_{t+1} + \gamma v_k (S_{t+1})$ 중에서 최고 값($max$)으로 업데이트 하면 된다. 즉, 정책 이터레이션에서 다음 상태들을 다 고려해서 업데이트 했던 것과는 다르게 그냥 제일 높은 값을 가지는 값으로만 업데이트한다.

다이내믹 프로그래밍의 한계와 강화학습

1. 다이내믹 프로그래밍의 한계

• 계산 복잡도
• 차원의 저주
• 환경에 대한 완벽한 정보를 알 수 없음

2. 강화학습

MDP에서는 환경에 대한 모델(상태 변환 확률, 보상)이 필요하다.
실제 환경에서는 모델을 정확히 알 수 없다.

강화학습은 모델 없이 환경과 상호작용하여 입력과 출력 사이의 관계를 학습한다.

정리

다이내믹 프로그래밍과 그리드월드

다이내믹 프로그래밍 : 순차적 행동 결정 문제를 벨만 방정식을 통해 해결

다이내믹 프로그래밍 1 : 정책 이터레이션

정책 이터레이션

• 정책 평가 : 현재 정책에 대한 참 가치함수 구하기
• 정책 발전 : 정책 평가를 기반으로 정책을 업데이트
• 정책은 확률적 -> 벨만 기대 방정식을 이용하여 최대의 보상을 얻는 행동 선택 (탐욕 정책 발전)

다이내믹 프로그래밍 2 : 가치 이터레이션

가치 이터레이션

• 정책은 확정적 -> 최적 정책을 가정하여 벨만 최적 방정식 이용
• 정책이 직접 주어지지 않고, 가치함수를 통해 행동 선택

다이내믹 프로그래밍의 한계와 강화학습

• 다이내믹 프로그램의 한계 (계산 복잡도, 차원의 저주, 환경에 대한 정보 필요)
• 모델 없이 학습하는 강화학습 등장