[강화학습 이론] 4장_강화학습 기초3 : 그리드월드와 큐러닝 1

슥슥·2023년 3월 28일

강화학습

강화학습 기초 스터디

목록 보기

3/7

4장. 그리드월드와 큐러닝

강화학습은 환경의 모델을 몰라도, 환경과 상호작용해서 최적 정책을 찾는다.

예측 : 환경과 상호작용하면서 정책에 대한 가치함수를 산출 (=정책 평가)

몬테카를로 예측
시간차 예측

제어 : 가치함수를 토대로 정책을 발전시켜 나가서 최적 정책을 학습 (=정책 발전)

살사 (시간차 제어)
큐러닝 (살사의 한계 극복/offpolicy 제어)

강화학습과 정책 평가 1: 몬테카를로 예측

1. 사람의 학습 방법과 강화학습의 학습 방법

강화학습이 학습하는 입력과 출력의 관계란??

입력 : 에이전트의 상태 & 행동
출력 : 보상

기존 다이내믹 프로그래밍은 모든 경우의 수를 생각, 계산해서 가치함수를 찾아내는데,
강화학습은 에이전트의 경험을 토대로, 어떻게 행동을 선택할지를 학습하는 것이다.

사람이 학습을 할 때 모든 상황을 다 계산해서 선택하지 않고, 행동을 해보면서 어떻게 고쳐야하는지 생각하는데, 강화학습은 이러한 학습 방법을 사용한다.

2. 강화학습의 예측과 제어

이전에 봤던 다이내믹 프로그래밍의 정책 이터레이션을 생각해보면, 정책 평가와 정책 발전 과정으로 이루어진다.

정책 평가할때 벨만 기대 방정식을 이용하는데, 앞에서 보았듯이 환경에 대한 모든 정보를 아는 것은 거의 불가능하다. 그렇기 때문에 정확하지 않더라도 적당한 추론을 통해서 효율적인 예측을 해야한다.

그럼 어떻게 예측을 할 것인가? 강화학습은 사람이 학습하는 방식과 유사하게, 틀리더라도 일단 경험을 해보는 방식을 통해 가치함수의 값을 에측한다.

3. 몬테카를로 근사의 예시

몬테카를로 근사 : 무작위 샘플링을 통한 추정

Ex) 원의 넓이를 구하는 방정식을 몰라도 무수히 많은 점을 찍으면(샘플링) 원의 넓이를 간접적으로 계산 가능

즉, 방정식을 몰라도 여러번 반복, 샘플링을 통해 답을 구할 수 있음!!!

4. 샘플링과 몬테카를로 예측

정책 이터레이션의 정책 평가에서는 몬테카를로 근사로 가치함수를 어떻게 추정할까?

가치함수 추정 과정에서 샘플링은 에이전트가 환경에서 에피소드를 한번 진행하는 것이고, 샘플링으로 얻은 샘플들의 평균으로 가치함수의 값을 추정한다.

가치함수의 정의를 다시 보면 다음과 같다.

v_\pi(s) = E_\pi[R_{t+1}+\gamma R_{t+2} + \gamma^2 R_{t+3} ... |S_t=s]

이건 사실 현재 상태로부터 받을 보상을 시간별로 할인해서 기댓값을 구한 것이다.

기존에 정책 이터레이션에서는 이 가치함수를 구하려고 벨만 기대 방정식을 사용했고, 가치함수 정의를 생각해보면 알 수 있듯이, 결국 계산을 한 기댓값이다. 그런데 샘플링을 해서 계산하지 않고, 예측을 하려면 어떻게 해야할까?

현재 정책으로 쭉 따라갔을 때 받는 보상들에 할인율을 적용해서 더한 값을 우리는 반환값이라고 부르기로 했는데, 현재 정책으로 에피소드를 쭉 진행하면 에피소드 동안 지나가는 각 상태마다 반환값이 존재한다.

<현재시점 t에서 최종 상태 T까지 현재의 정책에서 얻을 수 있는 반환값>

G_{t}=R_{t+1}+\gamma R_{t+2} + ... +\gamma^{T-t+1} R_T

아까 말했듯이, 한번 에피소드를 진행해보는게 샘플링을 하는 과정이다. 그럼 당연하겠지만, 한번 에피소드를 진행한다고 해서 전체의 기댓값을 추정할 수는 없고, 각 상태에 대한 반환값들이 많이 모여야 가치함수를 추정할 수 있게 된다.

위에서 말했던 것처럼 가치함수를 구하기 위해서 원래는 벨만 기대 방정식을 사용했다.

<벨만 기대 방정식>

v_\pi(s) = \sum_{a \in A}\pi_{(a|s)}(r_{(s,a)}+\gamma \sum_{a^{'} \in A}P^{a}_{ss'}v_{\pi}(s'))

이걸 계산하려면 상태 변환 확률( $P^a_{ss'}$ ), 보상함수( $r_{(s,a)}$ ) 를 알아되는데, 이걸 안다는 거는 원의 넓이를 구할 때 원의 넓이 방정식을 이미 알고있다는 것과 동일한 의미이다.

아까 말했지만, 몬테카를로 예측에서는 이걸 일일이 계산해서 기댓값을 구하는 방식으로 가치함수를 구하지 않고, 여러 에피소드를 진행해서 얻은 반환값을 기반으로 평균을 통해서 $v_\pi$ 를 계산한다.

<여러번의 에피소드로 s라는 상태를 방문하여 얻은 반환값들의 평균>

v_\pi \sim \frac{1}{N(s)} \sum ^{N(s)}_{i=1} G_{i}(s)

N(s) : 상태\ s를\ 방문한\ 횟수 \quad G_i(s) : s를 방문한\ i번째\ 에피소드에서의\ 반환값

말로 풀어서 설명을 해보자면, 3번의 에피소드로 $s_1$ 상태에서의 가치함수를 계산하고자 할 경우, $G_1(s_1)$ , $G_2(s_1)$ , $G_3(s_1)$ 를 구한 뒤에 평균을 통해 $s_1$ 에 대한 가치함수 값을 얻을 수 있는 것이다.

이런 에피소드를 무수히 많이 반복해보면, 충분히 반환값들이 많이 쌓일 것이고, 이 반환값들의 평균을 구하면 가치함수의 값을 얻을 수 있다!!!

다시 한번 풀어서 적어보자. 쭉 따라오면 이해될 것임

V_{n+1}= \frac{1}{n} \sum^{n}_{i=1} \ =\ \frac{1}{n} \Bigl(G_n + \sum^{n-1}_{i=1}G_i\Bigl)\ =\ \frac{1}{n} \Bigl(G_n + (n-1) \frac{1}{n-1} \sum^{n-1}_{i=1}G_i\Bigl) \\ \\ \ \\ = \frac{1}{n} \Bigl(G_n + (n-1)V_n \Bigl) \ =\ \frac{1}{n} \Bigl(G_n + nV_n-V_n\Bigl) \ =\ V_n + \frac{1}{n}\Bigl(G_n-V_n\Bigl)

이 식의 형태를 보면 새로운 반환값, 즉 새로운 에피소드를 수행할때마다, 어떻게 평균을 취하고 가치함수가 업데이트되는지 확인할 수 있다.

새로운 반환값 $G_n$ 이 들어오면, 기존의 가치함수 $V_n$ 에 $\frac{1}{n}\Bigl(G_n-V_n\Bigl)$ 를 더해서 $V_{n+1}$ 로 업데이트 하게된다. 즉, 이동평균의 방식으로 업데이트가 진행된다.

한 개의 상태 $s$ 의 입장에서 적으면 다음과 같다.

V(s) \leftarrow \ V(s) + \frac{1}{n}(G(s)-V(s))

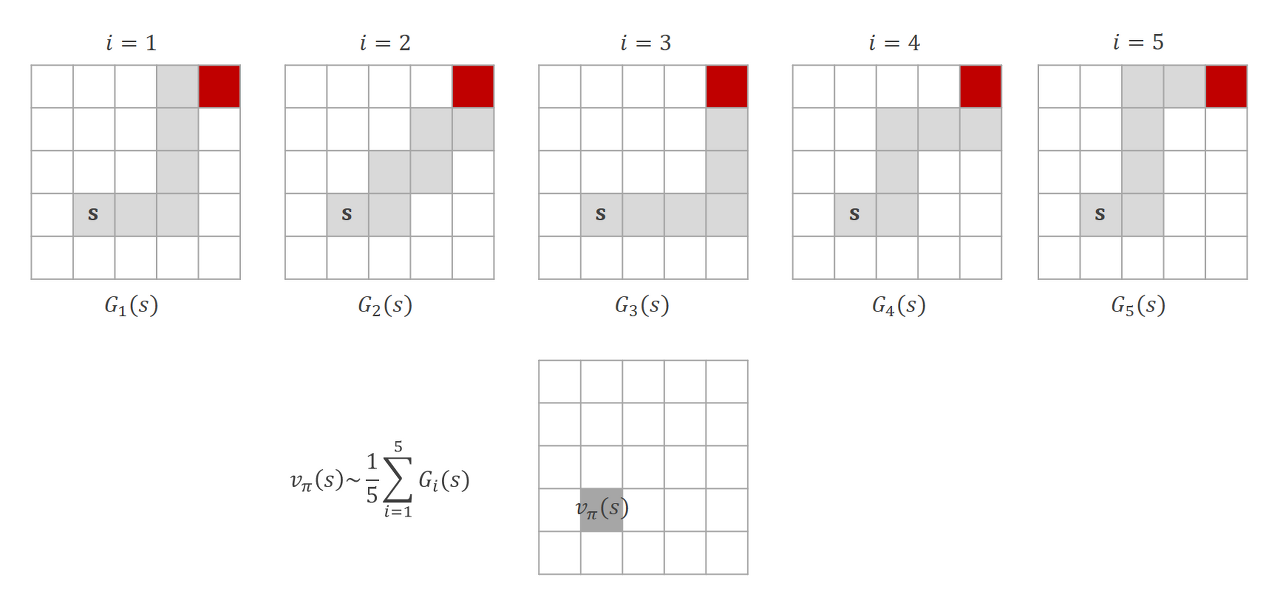
위의 그림을 보면 이해가 좀 쉬울것 같은데, 에피소드를 5번 수행했을 때, $s$ 라는 상태에서 가치함수의 값은 각 에피소드에서의 반환값을 평균내서 구할 수 있을 것이다.

$G(s)-V(s)$ 를 오차라고 하고, $1/n$ 은 오차항을 얼마나 반영할지 결정하는 Stepsize같은 역할을 하게된다. Stepsize는 $\alpha$ 로 표현하는데, 일반적으로 환경이나 적용하는 정책이 계속 변한다면 일정한 숫자로 고정하는게 일반적이다.

V(s) \leftarrow \ V(s) + \alpha (G(s)-V(s))

가치함수의 입장에서 결국 업데이트를 계속해서 구하려고 하는 값은 반환값이고, 에피소드마다, stepsize를 적용해서 조금식 가까워지게된다.

$G(s)$ : 업데이트의 목표

$\alpha (G(s)-V(s))$ : 업데이트의 크기

몬테카를로 예측에서 에이전트는 이 식을 가지고 지금까지 지나왔던 모든 상태들에 대해서 가치함수를 업데이트하고, 이는 현재 정책에 대한 참 가치함수에 가까워진다는 의미이다!

슥슥

이전 포스트

[강화학습 이론] 3장_강화학습 기초2 : 그리드월드와 다이내믹 프로그래밍

다음 포스트