[ML] AdaBoost

AdaBoost

부스팅 기법은 이전 모델이 틀렸던 예측을 보완? > 과소적한 훈련 샘플의 가중치를 높여서 새로운 모델을 만드는 기법 (아이디어) 를 사용한다.

이런 식으로 가중치를 업데이트 해가며 새로운 모델을 만드는 것이 AdaBoost 의 방법이다!

기본적으로 경사하강법과 비슷하지만 경사하강법은 하나의 모델을 대상으로 했다. 그러나 AdaBoost 의 경우 앙상블 모델인만큼 이전 모델을 버리지 않고 모두 앙상블로 사용해가면서 새로운 모델을 추가한다.

기본적으로 책에서 소개된 방법을 다시 말로 정리해보자.

1. J번째 예측기의 에러율을 계산한다. ($r_j$)
   예측기의 에러율 r은 모든 가중치를 더한 것을 분모로, 틀린 것의 가중치를 더한 것을 분자로 하여 계산한다.

2. 에러율을 이용하여 j번째 예측기의 가중치를 계산하자 (알파)
   예측기 가중치는 에러율이 높으면 (많이 틀린 예측기에 대해서) 가중치를 낮게, 에러율이 낮은 가중치에 대해서 예측기 가중치를 많이 준다

3. 다시 샘플로 돌아가 각 샘플의 가중치를 업데이트하자. (w 업데이트)
   이때는 예측이 틀린 샘플에 대해 가중치를 더 주는 방식을 사용한다. 예측이 맞았다면 가중치 유지, 예측이 틀렸다면 (기존 가중치) X exp(알파) 를 해준다. 이때 알파는 예측기의 가중치이며, 해당 예측기가 에러가 많으면

4. 샘플의 가중치를 정규화한다

AdaBoosting: Idea

• Strong model vs Weak model
  weak model(랜덤보다 조금 더 잘하는 예측모델) 의 경우 적절한 가이드만 주어지면 정확한 strong model 로 부스팅 될 수 있음.

• 어떻게? 어려운 케이스에 집중하는 방법으로.
  weak model 의 학습 데이터에 대해 reweight. 앞선 모델이 잘 풀지 못하는 케이스에 대해 가중치를 줌. (sequential)

AdaBoosting 을 수식으로 알아보자

• Input 을 정의한다
  인풋은 (x, y) 로 정의된 S이며, 정답값은 y로 (-1, 1) 의 분류문제를 푼다.
  

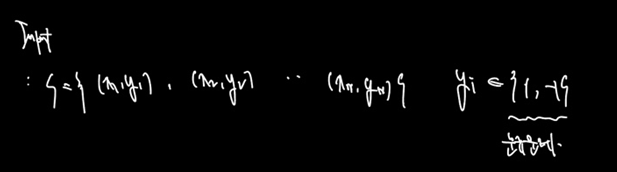
• 데이터셋 i 를 정의한다. ($D_1(i)$)
  $D_1(i)$ 는 첫 데이터셋의 example i 가 선택될 확률을 말한다. (선택될 수도, 선택되지 않을 수도 있으며 이는 각 샘플의 가중치로 정한다.)
  처음엔 모든 샘플의 선택 확률이 동등하겠다.
  

• 모델 $h_t$ 를 $D_t$ 를 가지고 학습한다.
  데이터셋으로 모델 h를 훈련시킨다. 기본적으로 AdaBoost 의 경우 StumpTree 를 많이 사용하며, 스텀프처럼 한 번 찍어 두 갈래로 분류하는 알고리즘이므로 매우 weakmodel 에 속한다. (Random보다 조금 나은 수준)
  

• 에러 $\varepsilon_t = P_D$ 를 정의한다.
  엡실론으로 에러를 정의한다. 에러란 실제 정답과 추정된 값이 다른 비율을 계산하는 것이며, 직관적인 계산(전체에서 틀린 개수를 세는)과 같다.
  

• 계산된 에러를 이용하여 해당 모델의 가중치를 계산한다.
  

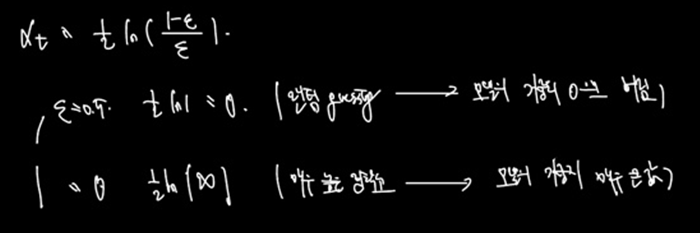
에러가 0.5라 했을 때는 해당 모델이 weak model 임에도 결국 random 과 다름없는 별로인 예측을 했다는 것으로 해당 모델의 가중치를 0으로 만든다.

에러가 0일 경우 해당 모델이 매우 좋은 정확도를 보임으로 모델의 가중치를 매우 큰 값으로 올린다.

• 모델의 가중치와 예측, 실제 값을 활용하여 새로운 데이터셋의 확률을 구한다.
  

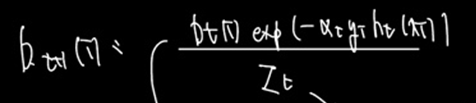
Z는 정규화를 위한 벡터값이므로 무시하자. 분자의 값을 보면

$D_t(i)$ 기존 t 시점의 데이터셋 선택확률이 기준이다. 이것에 곱하는 것들은
exponential 안의 값인데,
$-\alpha * y_i * h_t(x_i)$ 로 구성되어 있으며,
알파는 h모델의 가중치였다. h모델이 정확하면 그 모델을 믿고 각 샘플에 대해 변동성을 증가시키는 것이다.

결과적으로 예측이 맞은 경우 y * h(x) 가 1이므로 해당 샘플이 갖는 exp 안의 값은 음의 부호를 띄고, 예측이 틀린 경우 해당 샘플의 값은 양의 부호를 띄며 계산된다. 따라서 모델의 예측이 잘 맞은 경우 다음 데이터셋에서 선택될 확률이 떨어지고, 잘 맞지 못한 경우 선택될 확률은 증가한다. 이것은 한 모델 안에서의 이야기이도 전적으로 신뢰하는 것은 그래도 예측이 정확했던 모델이다.

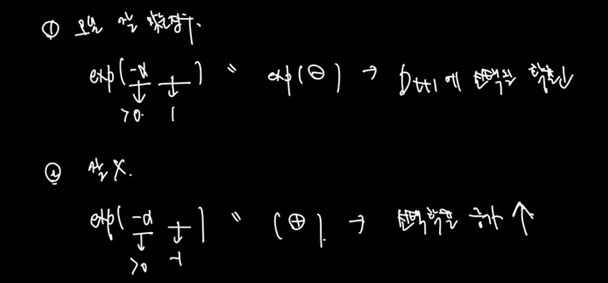
• 새로운 데이터셋에 대해 예측을 진행한다
  

결론

따라서 기존에 알고 있던 것과는 조금 다르게 부스팅 방법 역시나 sequential 하게 모델을 만들어가면서 샘플 선택의 과정을 거친다. 그러나 배깅은 복원추출 + 랜덤 선택이라면, 부스팅은 복원추출 + 가중치 확률을 조정한 선택으로 샘플링을 한다는 점이 차이였다. 그럼에도 훈련 세트 내에 가중치 조정이라 표현한 이유는 해당 가중치가 결국 선택의 확률이며 0으로 빠지면 그 가중치는 쓰지 않는 것으로 해석할 수도 있기 때문으로 여겨진다.

마지막 사진으로 부스팅의 방법을 정리하면서 글을 마친다.

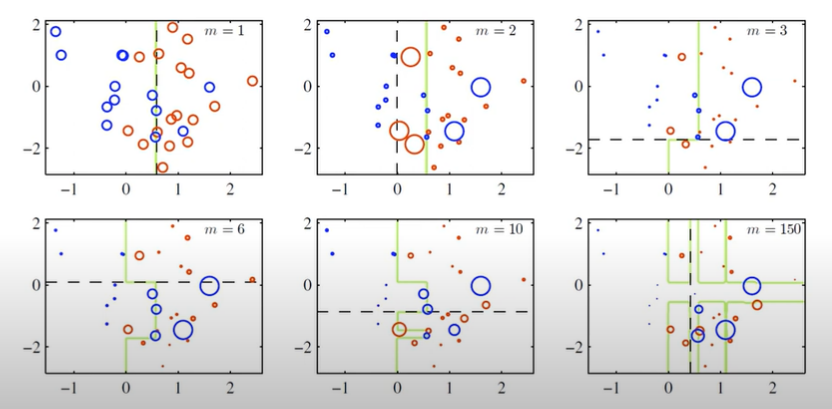
처음엔 단순 반으로 Stumptree. 반복을 거치며 잘못 분류한 것들을 더 선택, 잘 분류된 것들은 덜 선택하며 계속 Stumptree 를 만들어 나감. 만든 Stumptree 를 앙상블하면 정교한 모델 생성 가능!