[ML] 차원 축소 (PCA)

PCA의 목적?

적은 차원에서 서로가 직교하는 기저를 찾는 것, 원래 데이터의 분산을 최대한 보존하는.
예컨대 3차원 데이터에서 2차원 데이터로 축소하더라도 분산을 최대한 유지하자는 것.

그렇다면 어떤 기저가 더 선호될까? 적은 차원으로 투영했을 때 분산이 최대한 큰 것이 선호된다. 그림을 보자.

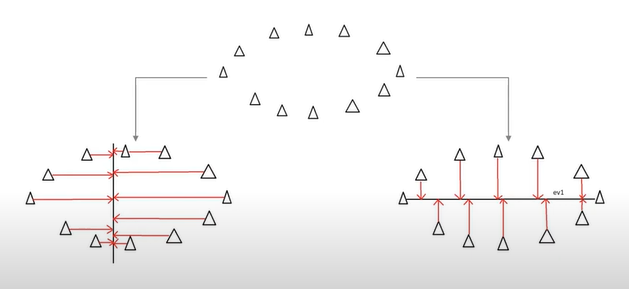
다음과 같은 데이터에서
1. 왼쪽과 같이 기저를 설정한 경우
2. 오른쪽과 같이 기저를 설정한 경우

오른쪽이 낮은 차원에서 더 높은 분산을 보인다. (데이터셋끼리 멀리 떨어짐)

따라서 차원을 내린 후에도 분산을 보존하는 basis 를 찾는 것이 목적이다. 아래의 식을 보자.

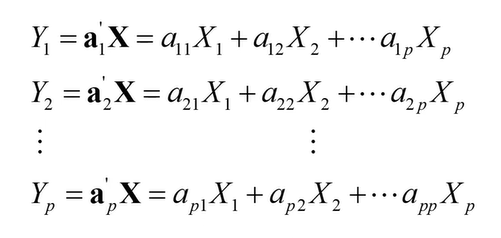
원래 변수는 X, 각 basis 의 벡터는 a, Y는 축소 후 나오는 분산의 값이다.

그렇다면 분산은 얼만큼 유지되는가?

분산의 보존량은 계산될 수 있다.

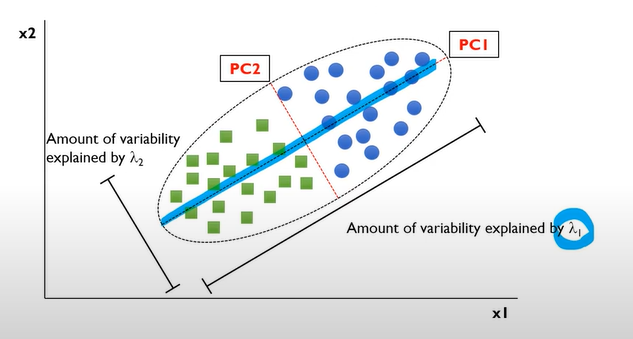
다음 그림에서

• PC1 에 사영했을 때의 분산의 양을 계산할 수 있다
• PC2 에 사영했을 때의 분산의 양을 계산할 수 있다

1. 공분산 행렬이란?

🤔공분산: 값 - 평균의 기대값. x,y 의 공분산은 x,y의 흩어진 정도가 얼마나 상관관계를 가지고 흩어졌는지를 나타냄.

• X: 데이터셋 (이 경우 각각의 컬럼이 객체이다: column-wise vector)
  

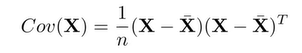
• $Cov(X)ij = Cov(X)ji$ : 대칭이다.

• $tr[Cov(X)] = Cov(X)11 + Cov(X)22 + Cov(X)33 + ... + Cov(X)dd$ : 전체 데이터의 분산은 공분산 행렬 대각의 합이다.
  

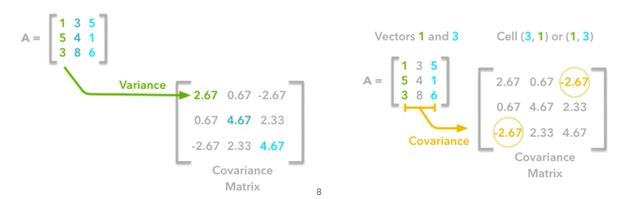
예컨대 하나의 전체 공분산 C는 다음과 같이 계산할 수 있다.

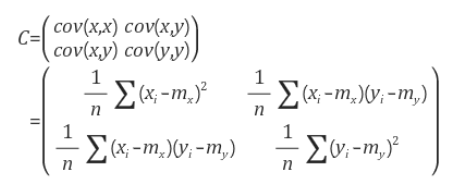
PCA란 입력 데이터들의 공분산 행렬에 대한 고유값 분해로 볼 수 있다. 결과로 나오는 고유벡터가 주성분 벡터 = 데이터의 분포에서 분산이 큰 방향을 나타내고, 고유값이 분산의 크기를 나타낸다.

2. 사영?

b라는 벡터를 a라는 기저에 사영시키자. x는 a의 방향을 가지고 있으면서 p라는 가중치를 갖는 벡터가 된다.

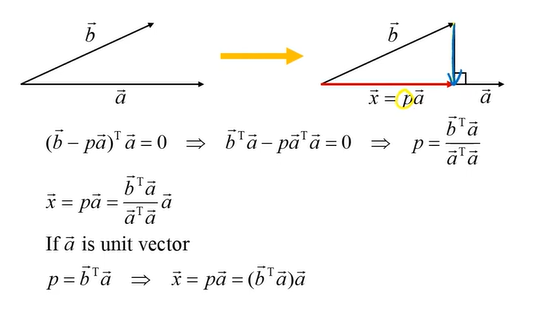
따라서 파란색 벡터는 b-pa 가 된다. 이를 a에 대해 정리하자.
만약 a가 unit vector 라면 p를 위와 같이 단순화할 수 있다.

따라서 b가 원 데이터 x, a가 Principal Component, p가 사영 후 값이 된다.

3. Eigenvalue?

Eigenvalue, eigenvector 은 고유값, 고유벡터를 의미한다. 하나의 매트릭스 A가 주어지면 스칼라 값 람다(고유값)와 벡터 x(고유벡터)를 갖는다.

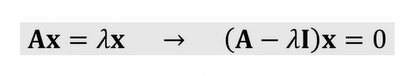
• 파란색은 크기만 바뀐다, 고유값을 말한다.
• 빨간색은 방향도 바뀐다

이제 PCA를 알아보자

1. 데이터의 평균을 0으로 맞춰주자
   

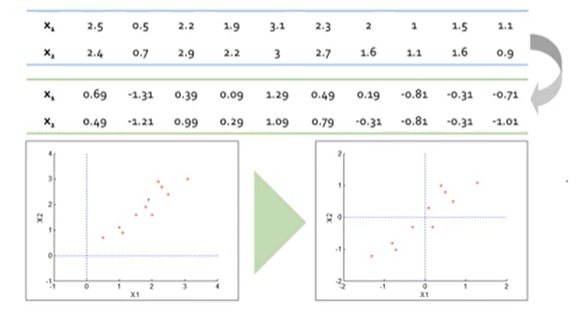
공분산을 구할 때는 각 값 - 평균이므로 이 평균을 0으로 맞춰주는 것이 centering 의 과정이다.

2. 최적화 문제를 정의하자

• 벡터 x가 w의 basis 에 사영되었을 때, 사영 이후 분산은 다음과 같다.
  

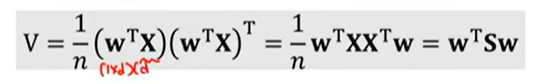
왼쪽의 식 => (1,d)(d,d) , (d,d)(d,1) = (1,1) 의 스칼라 값.

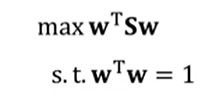
X와X^t는 S가 된다.

V를 최대화 시키기 위해서 w^Sw 를 최대화하는 w를 구하는 문제로 볼 수 있으며, 이제 라그랑지안을 도입할 수 있다.

3. 라그랑지안 문제를 푼다
   

S는 람다와 같다.

주성분 분석의 해는

• w 는 S의 고유벡터
• 람다는 S의 고유값이 된다.

• 몇 개의 주성분을 사용할 것인가?
• 원래 변수의 몇 %가 보존되는가?
  

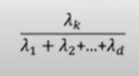
사실 강의와 구글링을 거쳐가며 여기까지 적었지만 타고 내려가니 고유값과 고유벡터란 개념이 나왔고 확인해보니 아직 모르는 개념이라는 걸 알았다. 고유값과 고유벡터를 이해하고 다시 올라가려 했지만 또다시 이해가 되지 않았고 문제는 행렬에 대한 기본 지식이 부족하고 그냥 처음부터 알아가야 한다는 느낌이 들었다.. 그래서 일단 여기까지 정리해두고 나중에 돌아올 질문들을 던져두는 것으로 하자.

• 고유값과 고유벡터가 뭐지?
• 왜 하필 공분산 행렬에 대한 분해일까?
• 왜 고유벡터가 방향이고 고유값이 크기로 연결될까?