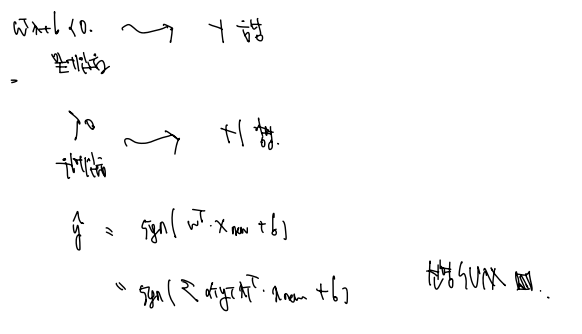SVM 의 수학적 배경을 따로 정리해보자.
순서는 다음과 같다.
선형 SVM
선형이 아닌 것을 선형 문제로 풀기
비선형 SVM
SVM 정확히 하기
사실 마진을 최대로 한다라는 멋지고 간단한 아이디어라 무시하게 되는 감이 없지 않아 있지만 정확히 마진을 무엇으로 정의할지, 식이 의미하는 것은 무엇일지 몰랐는데 정리할 수 있게 되었다.
기본적으로 2가지 클래스로 분류하는 상황을 보면, 특성이 2개더라도 특성이 나타내는 클래스를 구분하기 위해 1, -1을 추가로 주는데, 이같은 이유로 3차원 공간이 되는 것이다. (특성이 2개인데 왜 3차원이 되느냐에 대한 답이다.)
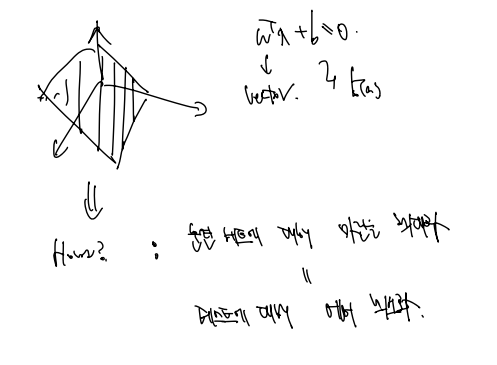
다음과 같은 3차원 공간에서 분류를 위한 식은 다음과 같다.
- x는 샘플
- w는 벡터(직선 또는 평면의 기울기)
- b는 bias 를 뜻한다.
x 샘플을 집어넣고 반환하는 값 (-1 또는 1) 에 따라 분류하는 것이다.
그런데 역시나 문제는 다음 함수를 어떻게 정의하느냐 하는 것이다. 정확한 워딩으로 최대한 정리하면
- 훈련 세트에 대해 마진을 최대화하는 w와 b값을 찾아야 하고
- 다른 말로는 테스트 세트에 대해 에러를 최소화하는 w, b값을 찾는 것이다.
다음 함수에 대한 아이디어에서 마진의 중요성을 느꼈다면 마진을 정의해봐야 함을 느꼈을 것이다. 마진을 수학적으로는 어떻게 정의할 것인가?
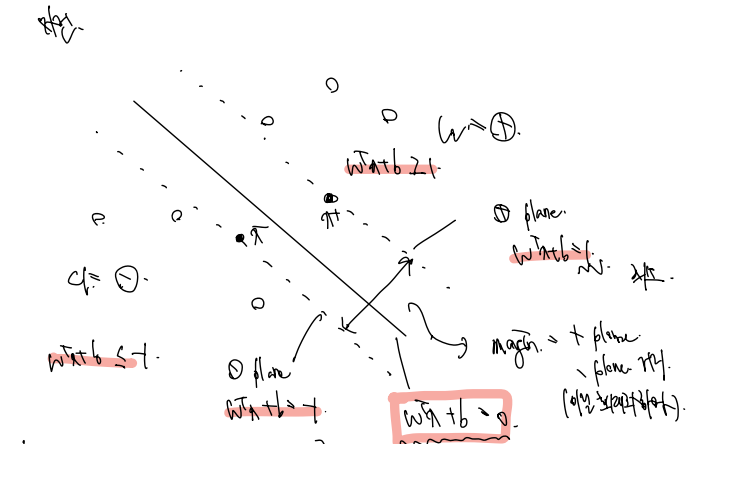
다음과 같은 샘플들과 함수 하나가 있다고 하자. 함수의 정의에 따라
Wx + b = 0 을 만족하는 점들은 함수 위에 있으며,
Wx + b >= 1 의 점들은 plus plane (양성 클래스에 속하고)
Wx + b <= -1 의 점들은 minus plane (음성 클래스에 속한다.)
왜 하필 1이냐에 대한 대답은 1 정도 떨어져있으면 구분할 수 있어 마진이라고 그냥 그렇게 설정한 것이기 때문이다.
또한 정확히 plus/minus plane 위의 점들은 Wx + b = 1, -1 을 만족할텐데, 이 점들을 각각 x+, x- 라 하자. (동시에 이 점들은 support vector 이다.)
그러면 정확히 마진에 대한 정의를 다시 내릴 수 있게 된다. 마진은 plus plane 부터 minus plane 사이의 거리이며, 이는 x+, x- 사이의 거리와 같다. 목표는 이것을 최소화하는 것이다!
또한 이렇게 되면 마진을 w로 표현해내는 것이 가능해진다. 왜 마진을 w로 표현해야 하냐고? 마진을 최대화하는 w를 찾고싶어서이다! 마진을 w로 표현해놓고, w를 조작하는 식을 앞으로 보게 될 것이다.
support vector 관계 정의, 람다 구해놓기
이후 마진을 정의함에 있어서 서포트벡터 간 관계를 이용하므로 서포트 벡터간 관계를 정의해보자. x+를 plus plane, x- 를 minus plane 바로 위에 있는 점이라 하였으므로 x+ 는 x- 를 평행이동한 관계로 정의할 수 있다.

여기서 w는 떨어진 방향을 의미하고, 람다는 그 폭을 결정한다.
x+ 를 처음 분류식에 대입하면 1값이 나온다. 대입한 식에서 위 관계를 이용하면 람다와 w만 남은 식으로 관계를 정의할 수 있다.
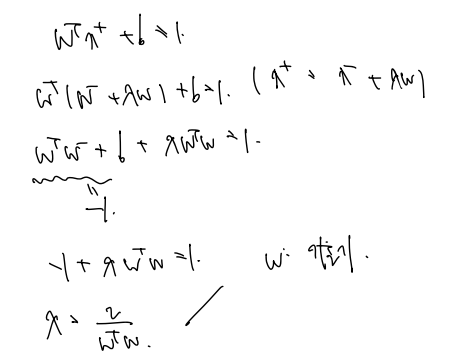
여전히 w는 벡터이자 기울기임을 알아두자!
P norm 과 이를 이용해 마진 수식화
서포트벡터를 수식으로 표현했으니 드디어 마진을 수식화할 차례다. (마진을 정의하는데 서포트벡터를 사용한다고 하였다.) 마진을 정의하기 위해서는 노름 개념을 알아야 한다. ||w|| 벡터노름에 대해 알아보자.
벡터노름은 다른 말로 P norm 이라 하며, 다음과 같은 식으로 정의된다.
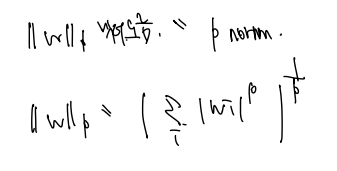
그 중에서도 우리는 L2 norm을 사용하며, 위 식의 p = 2 를 대입한 것! 이는 제곱하여 더한 것들에 제곱근을 해준 값이다.
따라서 라 정의할 수 있다!
마진을 정의하자면, 따라서
- 거리(x+, x-) 과 같이 정의할 수 있고
- 이는 L2 벡터노름으로 정의할 수 있다.
- 이 식을 x+에 x- 관계식을 대입하고, 람다를 구한 식을 대입하면 다음과 같은 w로만 정의된 마진을 확인할 수 있다.

이다! 여기서 우리의 목표를 다시 되돌아봐야 한다. 우리의 목표는 마진을 최대화하는 것으로, 다른 말로 ||w||를 최소화 하는 것이 목표임을 인지하자. 이를 식으로 나타내면
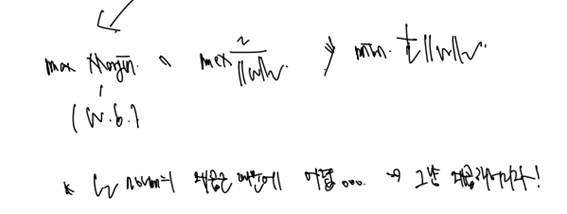
다음과 같다. 그런데 최소화 대상인 에 제곱근이 있는 게 마음에 들지 않는다. 그냥 제곱해버리자!
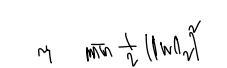
목적식과 제약식 정의, QP
이제 목적식과 목적식의 조건이 되는 제약식을 쓸 수 있다.
- 목적식은 초평면으로 정의된 마진의 역수이다.
- 제약식은 목적식의 조건으로 마진을 최소 1 이상으로 하라는 것이다.

결과적으로 2차식짜리 목적식 하나, 선형식인 제약식 하나가 등장하는데, 이를 QP라 한다. QP문서 참고
QP 는 Quadratic programming 의 약자로 목적식이 2차식, 제약식이 1차식인 convex 한 문제를 말한다. convex optimization 이란 QP의 문제를 푸는 것으로 최대, 최소가 1개만 존재하는 것을 말하고, 따라서 이 문제에서는 조건을 만족하는 w, b 가 1개의 값으로 존재하는 것을 알고 푸는 것이다.
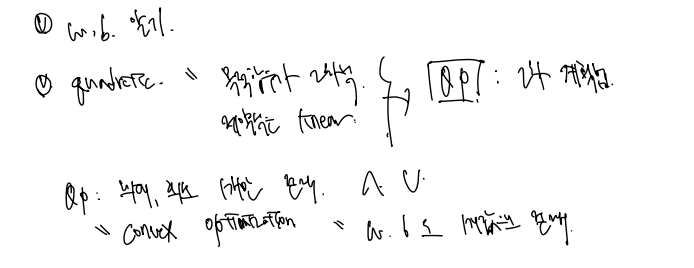
라그랑지안 승수 풀기
QP의 문제는 최소나 최대를 만족하는 값을 찾는 것으로 이를 라그랑지안 승수(multiplier) 로 표시할 수도 있다. 목적식과 제약식을 한 데 더하여 표현하는 것이다. 라그랑지안 문서
제약식이 부등식인 경우 -1을 곱하여 라그랑지안으로 표현하고, 우리가 풀어야 할 식은 다음과 같다. 최소를 만드는 w, b를 찾고, 최대를 만드는 알파값을 찾는 것이다.
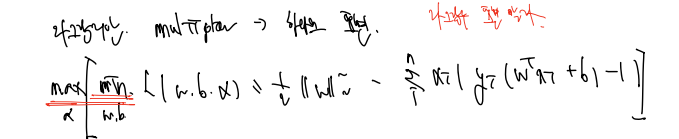
✅ min w, b 부분
역시나 2차이며 연속이므로 미분 = 0 이 되는 지점에서 최소값이 된다. 이를 이용하여 1. w에 대해 편미분 2. b에 대해 편미분 하면 관계식 두 가지를 찾을 수 있다.
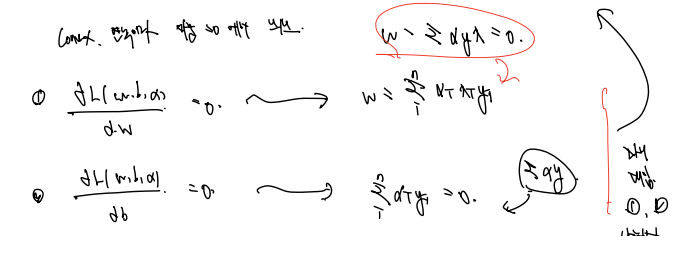
위에 나타난 관계식을 다시 라그랑지안 함수에 대입하자. 대입은 나줘서 1. 목적함수 부분과 2. 제약함수 부분에 각각 대입한다. w가 있는 위의 식에 적극적으로 우리가 편미분으로 구한 식을 대입하고, 알파와 y가 곱해진 곳에 0을 대입하면 어느정도 정리된 (복잡한?) 식을 얻을 수 있다. 전개 과정은 다음과 같다.

✅ max 알파 부분
위에서 풀었던 식을 정리하면 다음과 같다.
역시나 라그랑지안 함수를 푸는 것이며, 목적함수는 우리가 풀었던 식이며, 제약식은 (알파 * y) 의 합이 0 이라는 조건식이다.

여기서도 우리가 풀고자 하는 목적식은 (알파에 대해서 풀어야 하므로) 2차식이며, 제약식은 알파가 한 번 들어가있으므로 linear 하다. 따라서 여전히 QP 문제이며, 목적식을 최대화하는 알파는 1개다!
위 식의 dual 문제를 풀기 위한 조건으로 KKT condition 이란 게 존재하며, 조건 중 4번째 Comlementary slackness 의 식은 아까 봤던 다음 식이 = 0 이 되는 것이다.

w 구하기
다음 조건식을 푸는 과정에서 최종 결론이 도출된다.
✅ 알파 > 0 일 경우 : 뒤의 식 = 0
알파가 0보다 클 경우 뒤의 식은 꼭 0 이어야 한다. 뒤의 식이 0 이란 것은 결국 y(wx + b) = 1 이라는 것이며 이는 - - 든 + + 는 해당 샘플이 점 위에 있는 상태를 의미한다. 다른 말로 서포트벡터인 경우에 알파 > 0 이다.
✅ 알파 = 0 인 경우 : 뒤의 식 =/ 0
뒤의 식이 0 이 아니라는 것은 샘플이 서포트벡터가 아닌 상황을 말한다.
: x가 서포트 백터이어야 알파 >= 0 이다!
이를 아까 w를 구한 식에 다시 적용하면, 다음고 같이 전체 x를 모두 보던 범위에서 서포트벡터의 알파, y, x 만 보는 식으로 전환할 수 있다.

다른 말로 서포트벡터를 이용하여 w를 찾는 것이다!
b는 어떻게 구할까?
b 구하기
우리는 이전에 y = Wx + b 로 정의한 적이 있었다. 따라서 w를 우리가 구한 식으로 대체하고, 들어갈 x, y 는 서포트벡터 하나의 좌표를 이용하면
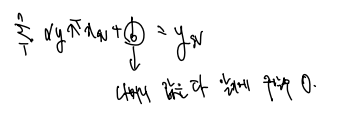
나머지 알파, y, x = w 이고 서포트벡터의 x, y 값은 알기에 b값도 구할 수 있을 것이다.