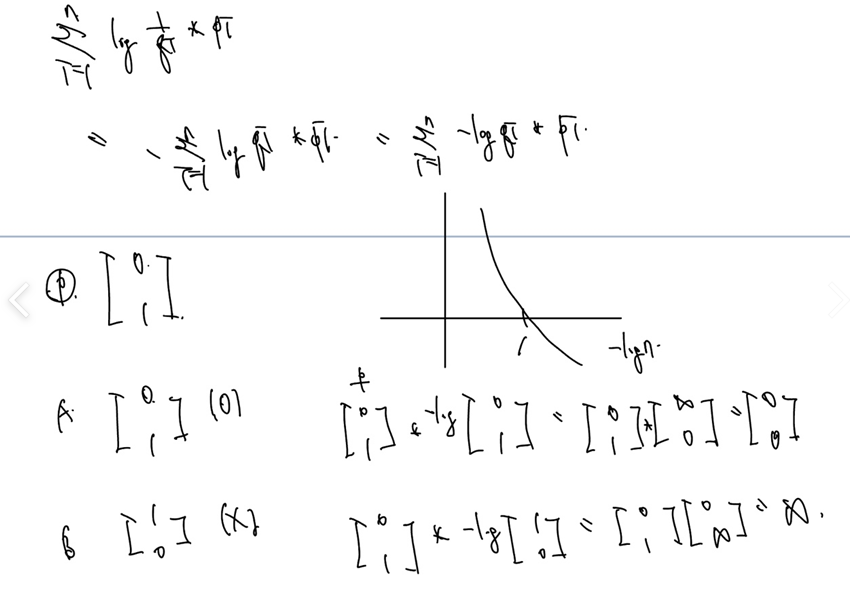소프트맥스와 크로스엔트로피는 처음 보기도 하고 와닿지 않아서 유튜브 영상 두 개를 보고 정리하는 글! 모두 허민석님의 유튜브를 참고했다.
그럼 시작하자!
로짓?
소프트맥스 함수에 대해 이해하려면 각 클래스에 대한 확률과 모든 클래스에 대한 확률을 구분해야 하고 그보다 먼저 로짓에 대해 이해해야 한다. 로짓이란 무엇일까?
간단히 말해 로짓(Logit)은 확률 p를 -(무한대) 부터 +(무한대)까지 바꿔주는 수이다. 그래프를 먼저 보자!
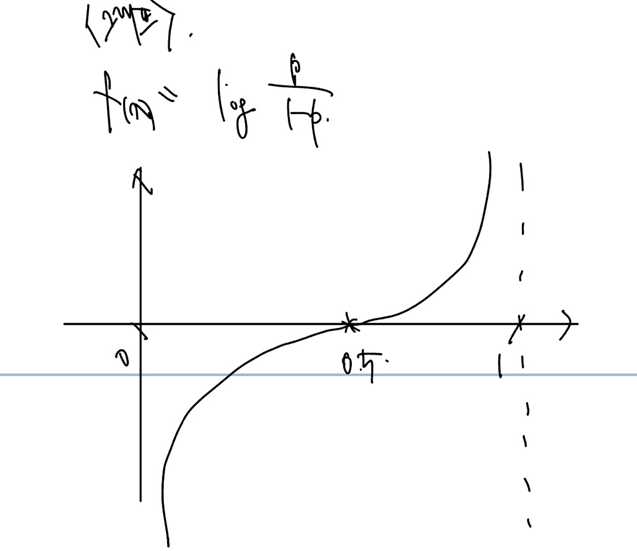
가로축은 확률 p, 세로축은 각각의 확률에 대응되는 로짓이다. 예컨대 확률이 0.5라면 0이 출력되고, 1에 가까워지면 무한대로, 0에 가까워지면 -무한대로 가까워진다.
위와 같이 확률 p가 주어지면, 로짓을 계산할 수 있고, 로짓이 주어지면 확률을 계산할 수 있다.
모델의 결과에 따라 로짓의 값이 강아지4, 고양이2, 토끼-2 라고 출력되었을 때, 로짓 값이 주어졌으므로 이를 확률로도 계산해볼 수 있다.

공식에 따라 이를 확률로 계산하고, 더하면 1이 넘어간다! 로짓으로 매칭되는 확률은 모든 클래스에 대한 확률이 아닌 각 클래스에 대한 확률이기 때문에 그러하다. 여기서 '모든 클래스에 대한' 과 '각 클래스에 대한'의 비교가 가능해진다!
그러므로, 소프트맥스는
소프트맥스는 방금 확인한 로짓을 e의 지수로 갖는 함수이다. 소프트맥스의 식과 그래프를 한눈에 보자.
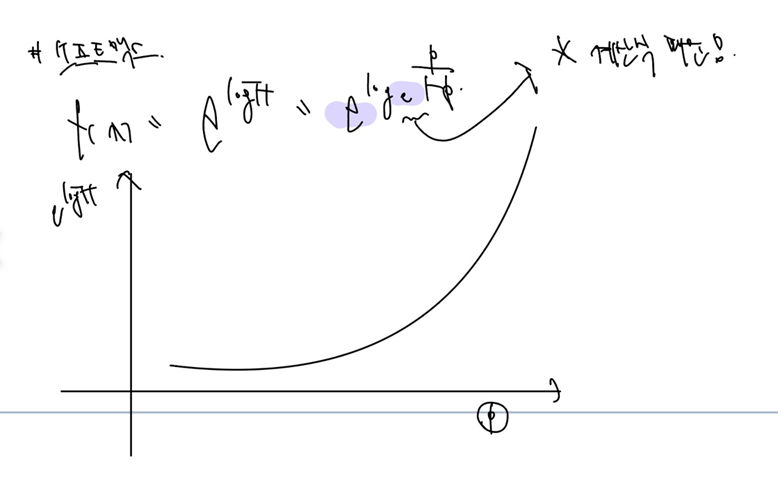
가로축은 확률 p이며, p에 따라 로짓이 계산되고, 로짓이 또다시 인풋으로 들어가면 소프트맥스가 계산된다. (참고로 e=2.71XXX..) p가 커짐에 따라 로짓도 커지므로 소프트맥스도 증가만 한다.
🤔왜 하필 로짓의 밑은 e일까? > 확률이 증가하면 그에따라 소프트맥스 역시 증가만 하면 되기 때문에 자유로운 수일 수 있지만 이미 로짓에 사용된 로그에 e가 사용되었다. 따라서 밑 역시 e로 주면 계산이 훨씬 쉬워진다!
이제 실제 계산을 해보자. 소프트맥스의 인풋은 로짓이랬다. 실제 각 클래스에 속할 확률은 모든 클래스를 더한 것을 분모에, 해당 클래스를 분자에 위치시키면 계산이 가능하다. 다음과 같다!
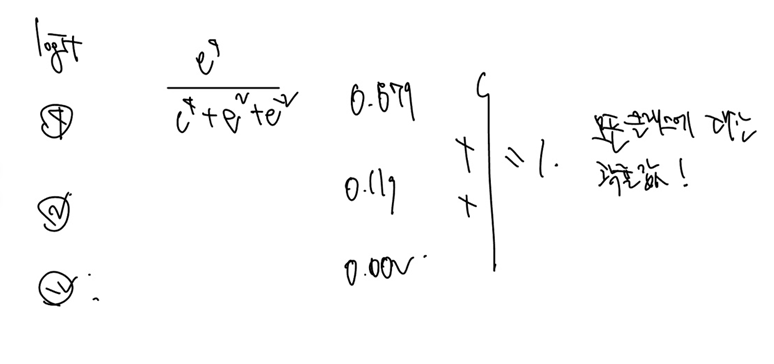
확률을 더하면 이번엔 1이되고, 다른 말로 소프트맥스에 따른 확률은 모든 클래스에 대한 확률값임을 의미한다.
크로스엔트로피
크로스엔트로피란 틀릴 수 있는 정보의 양을 의미한다. 그리고 이때는 소프트맥스로 예측한 확률과 실제를 비교하여 구한다!

다음과 같은 예에서 강아지 사진 하나에 대해서 소프트맥스를 활용한 예측Q를 실제 정답 P와 비교하는 것이다.
여기서 일반 엔트로피와 크로스엔트로피를 구하는 식을 보자. 여기선 크로스엔트로피를 구하는 식에 더 집중하자!
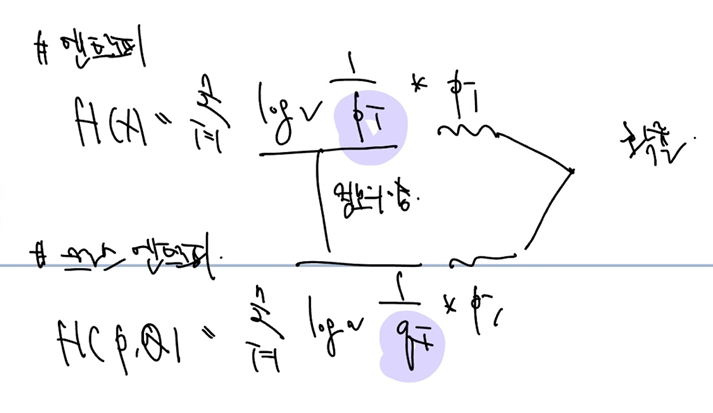
- 는 실제 확률을 의미한다.
- , 는 정보의 양을 의미한다. 바꿔말해 실제와 맞지 않을수록 엔트로피가 커진다고 생각하면 된다.
결국 엔트로피는 실제와 예측이 근사한지 따지는 것이고, 와 를 비교하는 것이다.
- 여기서 두 가지가 완전히 다르면 엔트로피는 무한이 되며
- 두 가지가 동일하면 실제 엔트로피 값과 동일하게 된다!
- 따라서 이다.
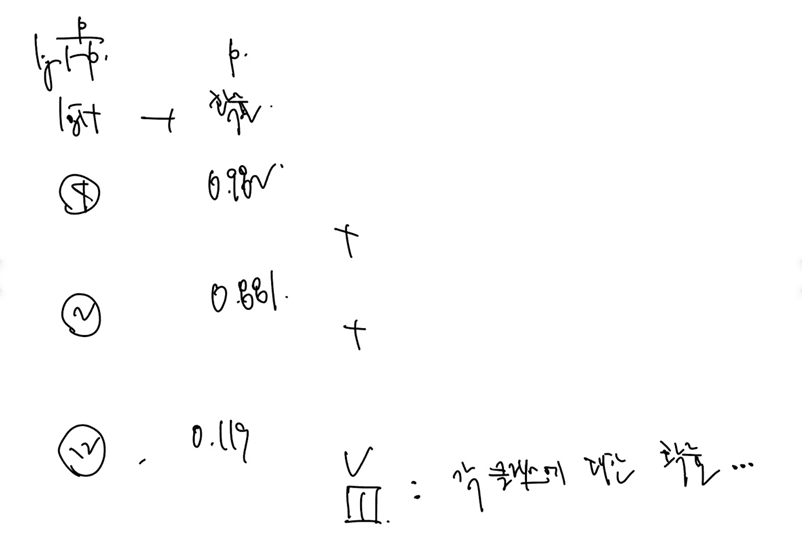
이제 식에따라 본격적인 계산을 해보자! 소프트맥스는 로그의 분자로, 실제값은 그냥 곱해주고 모두 더한 것이 엔트로피 값이다. (강아지 사진 하나의 샘플의 예측에 대한 엔트로피라 한다.)
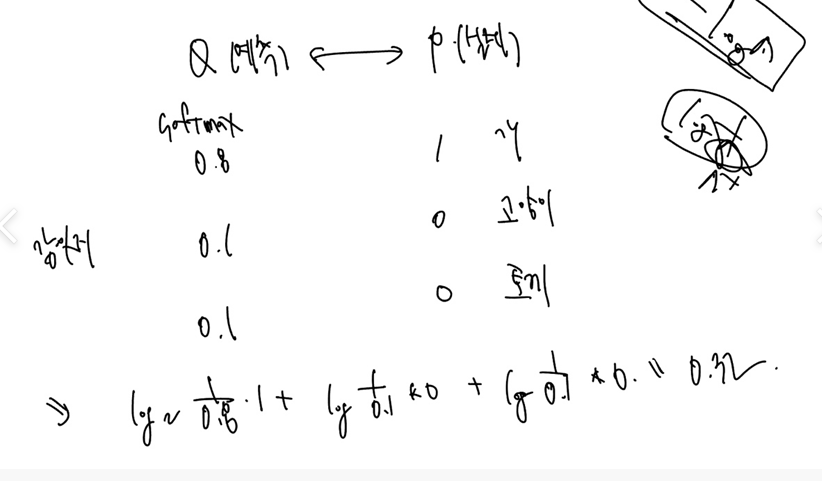
그런데 분모, 분자가 이해가 안되면 그냥 원래대로 - 로 생각할 수도 있다. (그래프로 연관지을 수 있어 좀 더 직관적이다.) 로그를 거꾸로 하면 -값을 꺼낼 수 있고, 다시한번 의 그래프를 그려볼 수 있다.
다음은 실제값 [0,1]에 대해 예측 [0,1] 과 예측 [1,0] 의 엔트로피를 계산한 것이다. 예측이 맞으면 엔트로피는 0(실제 엔트로피), 예측이 아예 다르면 엔트로피 무한이 되는 계산이다!