SVM 에 대한 이야기를 계속하자. 이전에 한 것은 선형 SVM 이야기이고, 이제 다음의 두 가지 방법을 볼 것이다.
- Linearly unseparable 한 문제를 선형으로 풀기 (soft margin SVM)
- 비선형으로 풀기 (kernel method)
Soft margin SVM
Soft margin SVM 은 선형으로 풀 수 없는 문제를 선형으로 다루는 것이다. 그 방법은 hard margin 이 아닌 soft margin 을 설정하여 마진 사이 에러를 허용하는 것이다.
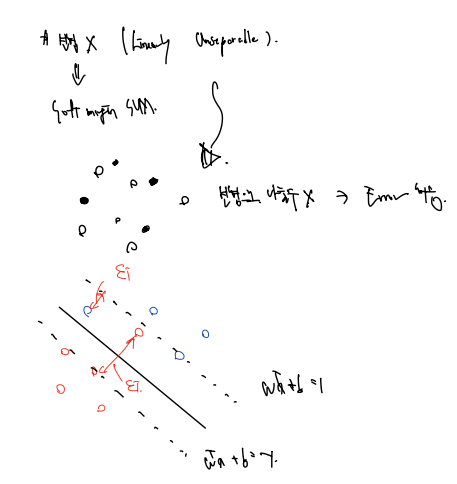
따라서 목적식은 기존 선형 SVM 의 목적식에 C (규제의 정도) , E (에러) 를 포함한 식으로 정의하게 되고, 조건은 1-E보다 커야 함으로 정의한다. 에러가 0이면 무조건 1보다 커야 함을 의미하는데, 에러가 있을수록 1보다 작아지기 때문이다.

목적식과 제약식은 다음과 같이 정의한다.
- 목표는 목적식을 최소화한느 w, b, e 를 결정하는 것이다.
- e>=0 를 도입한다는 것 = 에러의 허용 = 에러를 마냥 크게 해서는 안됨(이를 C가 조절)
- C가 마진과 에러에 대한 trade-off 를 결정한다.
C가 커질수록: 에러에 대한 제약이 많다 > 에러를 허용하지 않는다 > overfit
C가 작아질수록: 에러에 대한 제약이 많다 > 에러를 많이 허용한다 > underfit
라그랑지안으로, 문제 해결
역시나 다음 식을 라그랑지안으로 해결할 수 있다.
라그랑지안은 primal 문제는 최소화하고, dual 문제는 최대화해야 한다고 했다!
역시나 부등식이 있으므로 다음과 같이 정의할 수 있다.
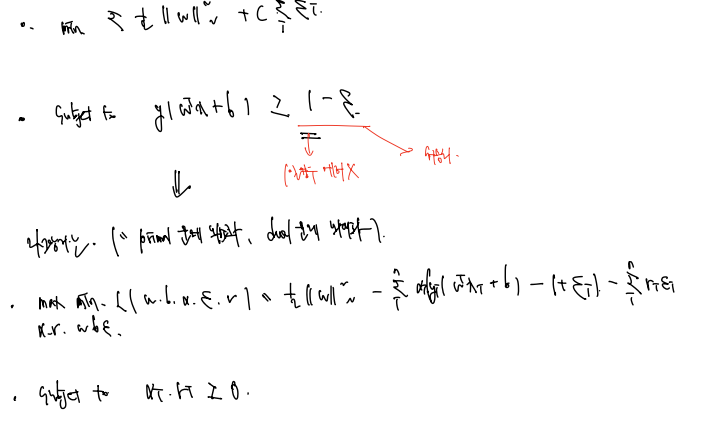
(추가된 r은 뭘까?)
✅ primal 문제 해결 (미분 = 0 에서 최솟값)
각각 w,b,e에 대해 편미분한 값을 이용하자. 편미분 한 결과는 다음과 같다.
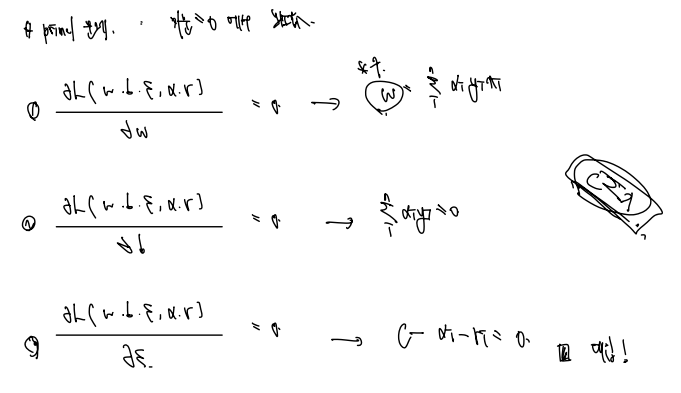
이 편미분한 값을 모두 primal 식에 대입하고 정리하면 다음과 같은 식을 도출할 수 있다.

이제 이 식에 대해 dual 문제를 풀어주자.
✅ dual 문제 해결 (KKT condition)
dual 문제를 해결함에 있어서 목적함수와 조건식을 다시 정의하는데, 이전 linear 문제와 한 가지 다른 것은 0<=알파<=C 조건의 추가이므로, 알아두자. 나머지는 다 같다!

역시나 이 식을 풀기위해 KKT 조건을 이용하고, 그 중 하나인 (가장 중요한) 조건은 다음과 같은 문제를 풀어야 한다.
기존식에 +e가 추가된 형태이며, r * e = 0 인 조건과 알파 = C-r 인 조건이 있다.
이제 알파에 따라 각각에 대해 풀어보자! 전개과정은 , 로 구분했다.
-
알파 = 0
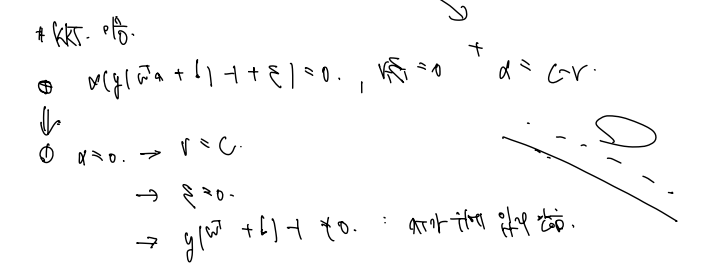
알파 0 > r = C 가 같음 , e = 0 , y(w + b) -1 =/ 0 : X가 plane 위에 있지 않다! -
0 < 알파 < C
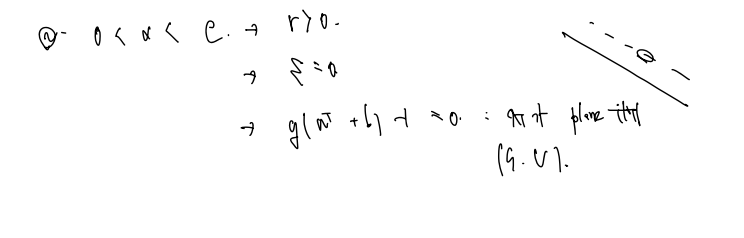
0 < 알파 < C , r > 0 , e = 0, y(w+ b) - 1 = 0 : X가 plane 위에 있다. (support vector) -
알파 = C
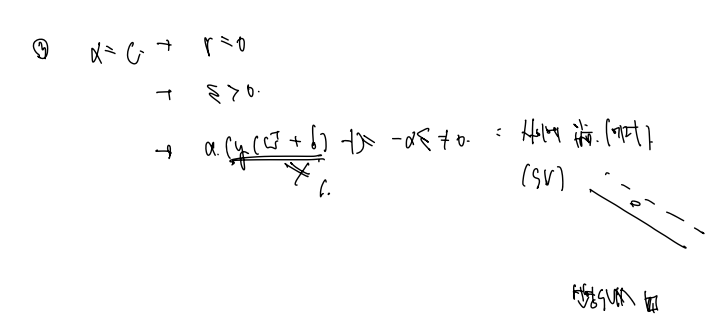
알파 = C, r = 0, E > 0, a(y(w+ b) - 1) = -ae =/ 0, y(w+ b) =/ 1 : X가 plane 사이에 있음 (에러 > 0 이므로)
kernel Method
다음과 같이 비선형의 구분선을 그으려면 어떻게 해야할까? > 일단 높은 차원으로 전환해야 한다.
차원을 전환시키려면 phi 함수를 이용한다. 예컨대 X > Z 로 변환하는 함수이며, (X1, X2, ... Xn) 에서 (Z1, Z2, ... Zn) 으로 바꾸는 것이다.
- P차원에서 Q차원으로 올리는 것과 같은 말이다.
- Q차원에서는 선형으로 분류할 수 있을 것이다.
- 다시 P차원으로 projection 하는 과정에서 비선형의 함수를 찾을 수 있다.
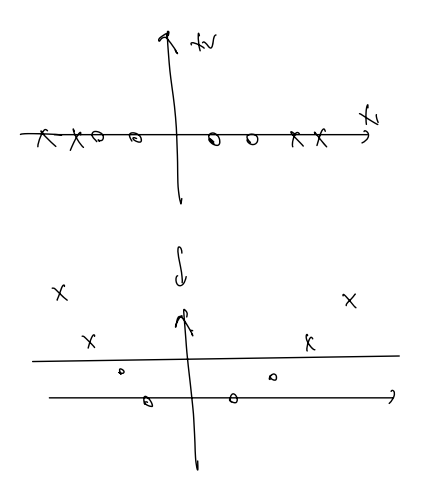
다음과 같은 과정이며, 예컨대 (X1, X2) 로 2D였던 변수를 (X1, X2, X1^2, X2^2, X1X2) 로 5D로 올려서 푼다. (분류는 쉬워지며, 효율적인 계산방법이 있다.)
여기서 목적함수를 다시 불러오고, 이를 phi를 적용한 함수로 바꿔보자.
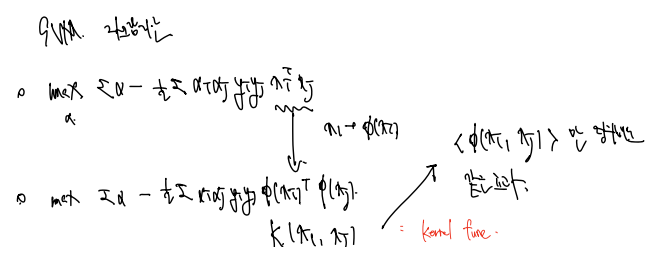
phi(Xi) * phi(Xj) = K(Xi, Xj) 로 정의하자. 같은 효과를 낼 수 있는 함수를 커널 함수라 하자!
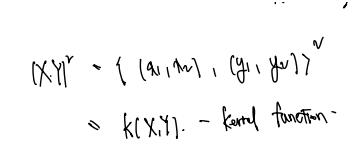
SVM 커널의 예는 다음과 같다. x, y 가 다음과 같이 라벨의 분류는 확실하나 x값이 같은 차원에서 분류되지 않는 값으로 주어졌다고 하자.
이때 Degree = 2 인 polynomial kernel function 을 만들어 계산할 수 있다.
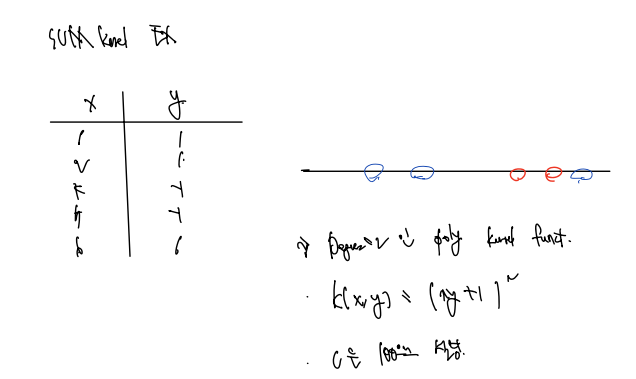
- K(x, y) = (xy + 1)^2 로 정의했다
- C = 100 으로 설정했다
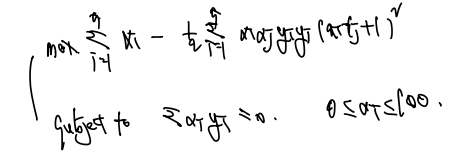
다음의 문제를 풀면 된다. 알아낸 알파값은 다음과 같다.

이제 위 함수에 알파, y, x 값을 집어넣고 계산하면
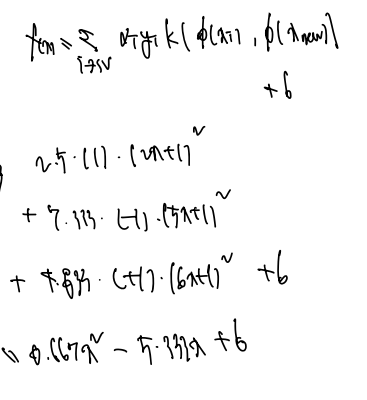
여기에 서포트벡터인 (알파가 0인 것) x=2, y=1 을 대입하면 b = 9 가 도출된다. 그럼 완전한 f(x)를 찾을 수 있다.
f(x) = 0.667x^2 - 0.533x + 6