[ML] 분산과 편향

분산, 편향이란?

머신러닝 분야에서 지도학습과 관련하여 에러를 측정하는 중요한 지표로 분산과 편향을 든다. 이번에 분산/편향을 살펴보는 것은 앙상블 기법을 공부하던 도중 대부분의 앙상블 기법이 편향은 조금 높이지만 분산은 낮춘다는 효과가 있다는 것을 확인했는데, 와닿지 않아서이다. 편향, 분산은 무엇이고, 어떤 관계가 있으며, 앙상블 기법과는 어떻게 연결될까?

우선 편향과 분산은 다음과 같이 정의해볼 수 있다.

지도학습에서, 예측값과 정답이 대체로 멀리 떨어져 있으면 결과의 편향이 높다고 말하고, 예측값들이 자기들끼리 멀리 흩어져 있으면 분산이 높다고 말할 수 있다.

단 두 줄로 깔끔히 정리되고 어느정도 이해가 되는데, 잘 이해했는지 그림으로 확인해볼 수 있다. 다음은 분산과 편향을 공부할 때 자주 나오는 과녁판 그림이다.

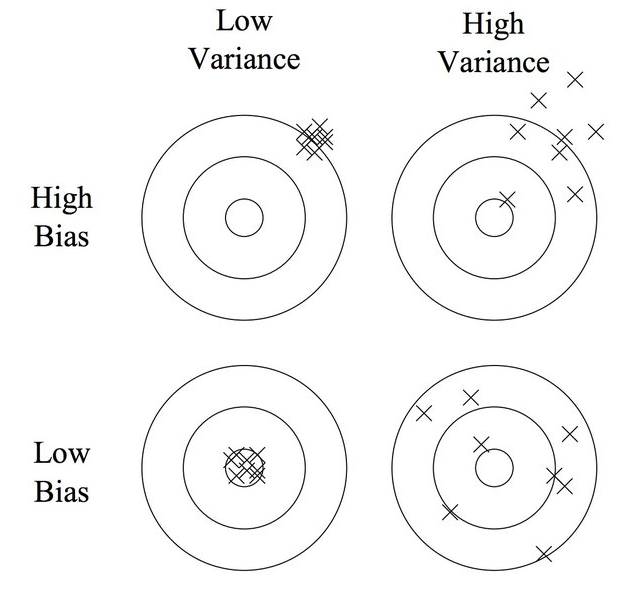
앞서 편향과 분산에서 중요한 키워드를 꼽으라면 예측값, 정답 이 되겠다. 위 그림에서 정답은 과녁의 중앙이며, 예측값은 과녁에 X값으로 표시된 것이다. 우리는 과녁판에 계속해서 활을 쏘면서 정답을 예측하는 것이다!

1. 왼쪽 위 상황은 어떤가? 과녁판 중앙과 예측이 대부분 멀지만 예측한 것끼리는 가까이 붙어있다. 이 경우를 높은 편향, 낮은 분산이라 할 수 있다.

2. 오른쪽 위는? 과녁 중앙에서 많이 벗어나있으면서도 예측한 것끼리도 멀리 떨어진 상황. 편향도 높고 분산도 높다.

3. 왼쪽 아래는? 과녁 중앙과 가까이 있으면서도 예측값끼리도 모여 있다. 낮은 분산과 낮은 편향.

4. 오른쪽 아래는? 과녁과는 상대적으로 가까우면서도 (위의 두 상황보단) 예측값끼리는 멀리 떨어져 있으므로 낮은 편향, 높은 분산의 상황이다.

이렇게 이해를 했다면 분산과 편향, 예측값과 정답의 대체적인 상황은 이해가 된 것이다.

수식으로 표현해보자

이렇게 이해한 내용을 바탕으로 분산과 편향을 각각 수식으로 나타내는 과정까지 가보자. x는 샘플, 함수 f 에다 넣은 f(x) 는 정답, f'(x) 는 예측값을 나타낸다. 그리고 E[f'(x)] 의 경우 모든 예측값들의 평균을 뜻한다.

편향을 수식으로 표현하면 어떨까? 기본적으로 우리가 알고 있는 오차와 같다. 오차를 계산할 때는 정답값-예측값들을 제곱해서 더하는 식으로 사용했고, 이는 한 번에 계산하면 다음과 같이 계산할 수 있다.

$(E[\hat{f}(x)] - f(x))^2$

예측값들의 평균에 실제 정답을 뺀 거리를 알려준다. 사실 모든 예측과 정답을 빼면서 더해가도 되지만, 평균을 사용한 것과 다름이 없기에 이렇게 표현한다. 부호를 감안하지 않은 순수 거리를 측정하기 위해 제곱해주었다. 이제 예측값과 정답이 얼마나 맞아떨어졌는지, 잘못 예측했는지 나타낼 수 있게 되었다.

분산은 어떠한가? 분산은 앞서 보았듯 정답과는 관련이 없는 수치이다. 그저 예측값끼리 멀리 떨어져 있으면 높고, 그렇지 않으면 낮은 것이다. 이 경우 예측값의 평균을 이용한다. 예측값의 평균에서 각 예측값을 뺀 값을 평균해주면 예측끼리의 떨어진 정도를 알 수 있다. 수식으로는 다음과 같이 표현한다.

$E[\hat{f}(x) - E[\hat{f}(x)])^2]$

각 예측값에 예측값의 평균을 뺀 것을 제곱한 것의 평균으로, 예측값과 예측값 평균 사이의 거리를 측정한다.

그러면 우리가 정의할 수 있는 에러는 이 둘을 합한 것이 된다.

$Error(x) = (E[\hat{f}(x)] - f(x))^2 + E[\hat{f}(x) - E[\hat{f}(x)])^2] + \sigma^2$

이때 시그마의 제곱은 무엇일까? 근본적인 오차를 의미한다. 무엇으로도 줄일 수 없는 오차를 말한다!

편향과 분산이 모델과 무슨 관련이 있는데?

사실 여기까지만 이해해도 짐작할 수 있겠지만 결국 예측값들의 모임이 우리가 만드는 모델이므로 편향과 분산은 실제 데이터(정답)과 모델(예측) 사이의 지표이다.

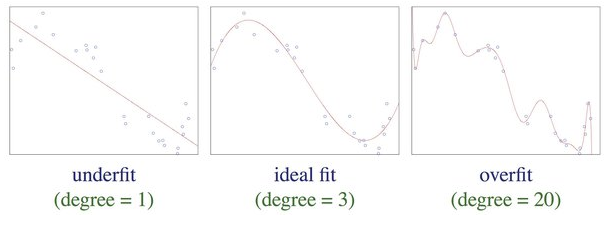
1. underfit
우리는 이미 모델이 샘플에 과소적합된 경우를 알고 있다. 모델이 샘플의 경향을 잘 담아내지 못하는 경우인데, 가장 왼쪽 그림과 같이 선형으로 단순한 모델은 샘플을 잘 표현하기가 어려워보인다. 이 경우는 과소적합이면서도 샘플과 모델의 거리가 멀어 편향이 높다고 말할 수 있다. 대신 선형으로 표현된 모델이므로 예측 사이의 거리는 멀어 분산은 낮다.

2. ideal fit
과대적합까지는 아니고 그래도 중간정도의 그림이면 새로운 예측이 들어오더라도 경향을 잘 반영한 예측이 될 수 있어 보인다. 따라서 이를 ideal fit 이라 하는데, 이 경우 모델은 중간정도의 편향, 중간정도의 분산을 보인다. (편향과 분산은 왜 꼭 trade off일까?)

3. over fit
오른쪽 그림과 같은 경우는 기존 샘플은 잘 담아내고 있지만 무언가 과해 보인다. 새로운 샘플이 들어왔을 때는 예측이 크게 벗어날 수 있어보이므로 이를 과대적합, 편향은 낮고 (정답과의 거리는 가깝지만) 분산은 큰(예측끼리의 거리는 먼) 상태라 할 수 있다.

이것이 분산, 편향과 과소, 과대적합 사이의 관계이다. 이제 왜 특히나 앙상블 모델에서 편향은 높아지고 분산은 낮아지는지 확인해보자.

그래서 앙상블에서는 왜 분산이 낮아지는데?

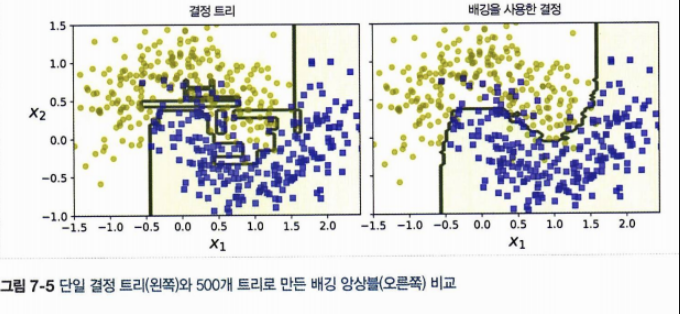
위 사진을 보면 쉽게 이해가 된다. 결정트리는 우리가 알고있듯 트리 깊이에 제한을 두지 않으면 끝없이 생성할 수 있어 과대적합의 위험이 있는 모델이다. 왼쪽 사진이 그것이다. 분류는 어느정도 잘 해낸 것 같지만(편향은 낮지만), 분산이 너무 높아 보인다. 이때 배깅 등 앙상블 기법을 적용하면 오른쪽과 같이 모델이 변한다.

결과적으로 여러 트리를 만들면 하나의 트리를 만들었을 때보다 각 트리의 예측값들을 또다시 평균하므로 어느정도 더 일반적인 모델을 만들 수 있다는 이야기이다. 일반적이라 하는 것은 과대적합에서 과소적합쪽으로 이동하고, (실제로 과소까지 오지 않겠지만) 편향은 조금 높아지더라도 분산을 낮추어 (예측 경계면이 부드러워지는 오른쪽의 그림을 보자) 더 일반화된 모델을 얻을 수 있는 것이다.

다시 돌아와서..

여기까지 왔다면 하나 궁금해지는 것이 왜 Variance 와 Bias 는 항상 Trade-Off 관계여야 하는 것일까? 같은 조건에서 둘 다 동시에 줄이는 방법은 없을까? 만약 트레이드오프 관계가 맞다면 대부분의 모델은 왼쪽 위의 그림 또는 오른쪽 아래 그림에서 움직여야 한다. 만약 이유가 데이터세트에 있다면 (데이터 셋을 따라가면 편향이 낮아지고 자연히 분산이 커지는 경우라면) 상대적으로 좋은 모델과 그렇지 못한 모델은 결국 데이터셋 분포에 달려 있다는 것인가? 이와 관련하여 답을 찾을 때 다시 포스팅 해보려 한다.