# ml01

The Perceptron

퍼셉트론은 딥러닝이나 머신러닝의 항상 첫 장에 등장하는 기초모형이다. 아래와 같은 퍼셉트론 모델에선 입력이 x1, x2 로 2개인데, 각각의 입력에 가중치를 곱한 값에 bias T를 더한 값을 sum 하고, 함수를 한 번 더 적용시킨다.

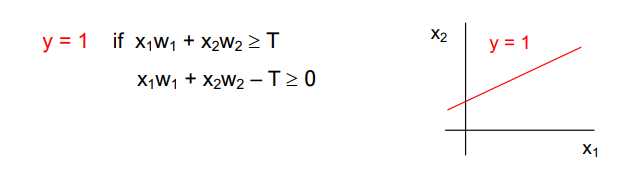
인풋과 가중치는 벡터로 다음과 같이 표현이 가능하다.

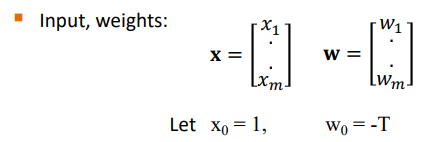
각각에 가중치를 더하여 곱한 값은 (여기선) z 라 하며, 한 번 전치시킨다. (weighted sum) 여기에 어떤 함수 (여기선 step function)을 적용시킨 값은 '예측'이다.

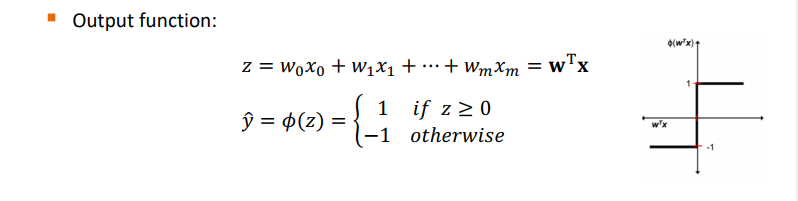
• 훈련 데이터

• 모델 w0, w1, w2 를 적절하게 찾으면 다음과 같이 분류를 한 번 할 수 있다.
  

• 따라서 적절한 w0, w1, w2 를 찾는 게 목표! 이런 과정을 '학습'이라 한다. (당연히 학습 데이터로 학습한다.)

Perceptron Learning

학습이란 훈련 데이터를 가지고,
1. 랜덤 w로 시작, 학습률을 가지고
2. 각각의 x에 대해 예측과 / 업데이트 수행

Perceptron Class

• z를 계산
• y' 을 계산
• fit

Irist 데이터셋에서 0, 2열을 가져오자. 100개의 데이터만 가져온다음 fit 함수를 만들자.

def fit(self, X, y):
  self.errors = []
  for _ in range(self.n_iter):
    errors = 0 
    for xi, target in zip(X, y): # x와 각각의 target 반복문
      update = self.eta * (target - self.predict(xi))
      self.w_[1:] += update * xi 
      self.w_[0] += update 

      errors += int(update != 0.0)

    self.erros_.append(erros)
  return self 

def net_input(self, X):
  return np.dot(X, self.w_[1:] + self.w_[0]) 

def predict(self, X):
  return np.where(self.net_input(X) >= 0.0, 1, -1) 

model = Perceptron(eta = 0.1, n_iter = 10) 
model.fit(X, y) 

Adaline

Adaptive linear neuron model 을 말하며, Activation 함수가 추가된 모델을 말한다. 비용함수를 정의하고 이를 최소화하는 것이 목표이다.

비용함수는 다음과 같이 정의한다.

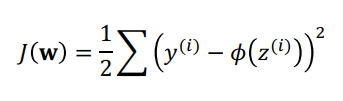
이를 최소화하기 위해선 가중치에 대한 변화가 필요하다. (비용함수에서 변수는 z이므로, 가중치가 변수로 관여하는 값이기 때문.)

가중치를 업데이트 하는 규칙은 다음과 같다.

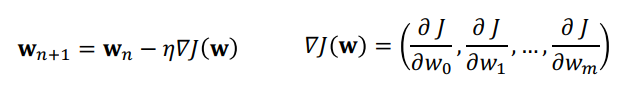
W^old 에서 W^new 로 업데이트를 진행하기 위해선 기존 w에 learning rate X 손실함수를 그 w 로 편미분한 값을 빼주면 된다. 왜? 편미분한 값은 결국 그 위치에서 이동해야 하는 값과 같기 때문이다. (양수면 왼, 음수면 오른쪽으로 이동해야 극소점에 도달함을 의미한다.) 따라서 미분한 값을 뺀 방향으로 반대로 이동하여 극소점에 도달하도록 할 수 있다.

The Adaline Class

def fit(self, X, y):
  self.cost_ = []
  for _ in range(self.n_iter):
    net_input = self.net_input(X) 
    output = self.activataion(net_input) 

    errors = (y - output) 
    self.w[1:] += self.eta * X.T.dot(errors)
    self.w_[0:] += self.eta * errors.sum() 

    cost = (errors ** 2).sum() / 2.0 
    self.cost_.append(cost) 
  return self. 
 

def net_input(self, X):
  return np.dot(X, self.w_[1:] + self.w_[0]) 

def activation( self. X):
  return X 
  
def predict(self, X):
  return np.where(self.net_input(X) >= 0.0, 1, -1) 

Limitation of Perceptron

퍼셉트론의 문제는 결국 선형함수만을 도출한다는 것이다. 우리는 데이터셋에 따라 선형이 아닌 문제도 풀 수 있어야 하는데, 퍼셉트론과 같이 간단한 구조에서는 이것이 불가능. 이러한 문제를 풀기 위해 퍼셉트론 여러 개를 합친 구조가 등장하였다.