[Mathematical Statistics] 3.5 Multivariate normal distributions

3.5 The multivariate normal distributions

multivarate standard normal distribution

정규분포에 대해 알았으니 이를 이제 d=1이 아닌 d=2, 3, ... 이상인 다차원으로 확장시켜야 할 때이다. 따라서 앞으로 소개될 내용은 multivariate, 다변량에서의 상황을 가정한다. 먼저 multivarate standard normal distribution (다변량 표준정규분포)의 내용을 보자.

Definition. Let $\mathbf{Z}:=\left(Z_{1}, \cdots, Z_{d}\right)^{T}$ be a random vector with $Z_{i} \sim N(0, 1)$ (Note: $E(\mathbf{Z})=0, Var(\mathbf{Z}) =I_d$ ) The joint distribution of $\mathbf{Z}$ is called the multivariate standard normal distribution (다변량 표준정규분포) and denoted by $\mathbf{Z} \sim N_d(\mathbf{0}, I_d)$.

• 확률벡터 $\mathbf{Z}$ 를 Z1, Z2, ..., Zd 인 d개의 확률변수를 묶어놓은 벡터라고 하자. 다변량의 시작은 여기서부터..

• 이들의 각 요소 Z1, Z2, ..., Zd가 standard normal distribution 을 따를 경우, 이들의 joint distribution 이 다변량 표준정규분포를 따른다는 것.

• 표시는 기존과 비슷해보이지만, normal distribution 에서 아랫첨자 d를 써서 d차원으로 확장되었음을 표시한다는 것과, 0은 일반적인 표시가 아니고 영벡터의 표시, 공분산 행렬로는 d차원 identity matrix 가 들어간다는 점에서 차이가 있다.

• identity matrix 는 다차원으로 확장하면서 본격적으로 등장하는데, 대각으로의 성분이 1로 채워진 행렬로 이해하면 된다.
  

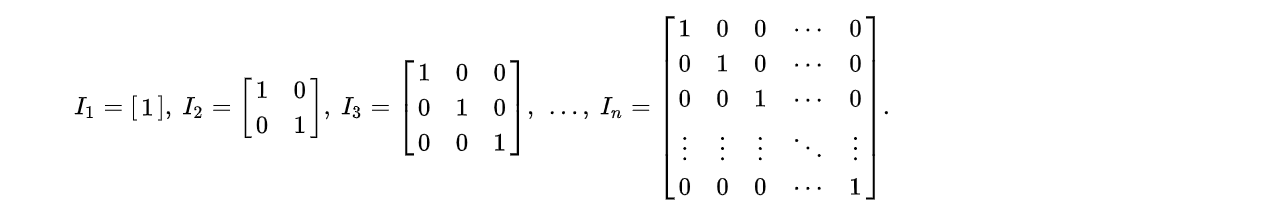
• $I_d$라 표시하면 dxd 행렬로 대각선이 1로 채워진 행렬이 될 것이며, 이것과 자기자신 행렬을 곱하면 자기자신이 튀어나올 것이다.

• 왜 Identity matrix 가 분산으로 사용될까? 알다싶이, 다차원으로 확장된 변수에서는 분산의 자리에 적절한 공분산을 써야 할 것이다. 그런데 각각이 N(0,1)을 따르는 변수에서는 diagonal 요소들이 모두 1로 채워질 것이다. 또한, off-diagonal 위치에는 이들의 공분산이 0이므로 0으로 채워질 것이다. 따라서 Identity matrix 가 튀어나오는 것.

The (joint pdf) of $\mathbf{Z}$ :

• joint pdf 는 변수 각각이 독립이므로 곱의 형태로 풀 수 있고,
• 첨자만 다르게 하여 normal distribution pdf 를 반복해서 곱해주면 된다.
• 마지막엔 서로다른 vi 표기대신 이들을 묶은 vector z를 사용하면 된다.

The (joint mgf) of $\mathbf{Z}$ :

• z는 d차원까지이므로 이 범위에서만 곱으로 연결해주면 되고,
• 이전에 normal distribution mgf 를 그대로 가져다쓰되 이걸 곱의 형태로 써주면 된다.
• 최종 형태도 그러함!

Fact. Spectral Decomposition Theorem (SDT)

스펙트럴 분해정리는 통계학 / 응용수학 분야에서 매우 자주, 유용하게 쓰이는 statment 다. 아래 정리와 fact 들을 아예 통쨰로 기억해두자. 핵심 요지는 real symetric matrix 가 있을 때 이걸 orthogonal 과 diagonal matrix 의 곱으로 쓸 수 있다는 것이다.

Fact (Spectral Decomposition Theorem). Let $\mathbf{A}$ be $d \times d$ a real symmetric matrix. Then there exists a $d \times d$ orthogonal matrix $\boldsymbol{\Gamma}$ (i.e.,$\Gamma\Gamma = I_d$ ) and $\boldsymbol{\Lambda}=diag({\lambda_1},{\lambda_2},{\lambda_3}..., {\lambda_d}$ with ${\lambda_1} > {\lambda_2}> {\lambda_3}> ...>{\lambda_d}$ such that

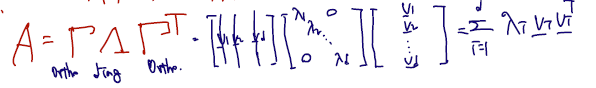
• 분해의 대상은 real 이고 symmetric 인 matrix A이다.
• A가 존재하는 한 orthogonal matrix 과 diagonal matrix 가 각각 존재한다는 뜻이고.. 특히 diagonal 의 경우 람다 간의 순서도 존재한다.
• 결국 symmetric matrix 를 적절히 orthogoanl matirx 와 diagonal matrix 의 곱으로 분해할 수 있다는 것이 중요하다.

아래 이어지는 statement 들도 중요하다. 알아두자.

Notes

• $\lambda_{i}$ 's are eigenvalues of $\mathbf{A}$ and corresponding eigenvectors are column vectors of $\boldsymbol{\Gamma}$.
  - 대각행렬의 요소인 람다들은 eigenvalues of A이고, 이들의 상응하는 컬럼벡터들은 orthogoanl matrix Gamma 의 열벡터들이다.

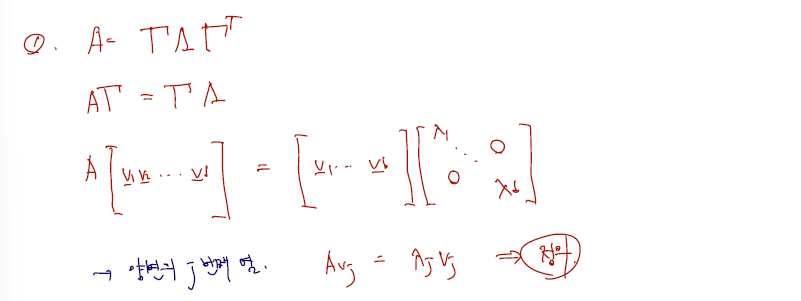
  • 어째서일까? eigenvalues, eigenvectors 들을 정의로 추출하는 과정을 따라가면 된다. 아래는 증명.
    

• If $\mathbf{A}$ is positive semidefinite, then it is known that ${\lambda_d} >= 0$, i.e., all eigenvalues are nonnegative.

• If $\mathbf{A}$ is positive definite, then it is known that ${\lambda_d} > 0$ , i.e., all eigenvalues are positive.

이에 대한 설명은 Matrix algebra를 담은 추가 포스트에서 깊게 다루도록 하자. 지금은 그저 matrix A를 decomposition 했을 때 람다의 bound가, matrix A의 bound 를 따른다.. (positive semidefinite 일 때 nonnegative, positive difinite 일 때 positive) 정도로만 하고 넘어가자. 나중 가서 알겠지만 그리 어렵지는 않다. 핵심은 A 가 psd일 때는 이를 S.D.T 해서 나오는 람다들이 음수승이기 어려우므로 0을 포함하지 않는다, 정도이다.

• We can define square-roots of positive semidefinite matrices. Let $\mathbf{A}$ be any $d \times d$ positive semidefinite matrix. By spectral decomposition,
  $\mathbf{A}=\boldsymbol{\Gamma} \boldsymbol{\Lambda} \boldsymbol{\Gamma}^{T}$
  for some $d \times d$ matrices $\boldsymbol{\Gamma}$ and $\boldsymbol{\Lambda}$ such that $\boldsymbol{\Gamma}^{T} \boldsymbol{\Gamma}=\mathbf{I}_{d}$ and $\boldsymbol{\Lambda}=\operatorname{diag}\left(\lambda_{1}, \cdots, \lambda_{d}\right)$. Note each $\lambda_{i}$ 's are nonnegative. Define $\boldsymbol{\Lambda}^{1 / 2}:= diag(각 람다의 square root)$ . Then,

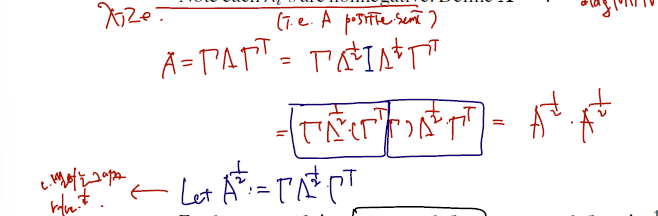
• A가 psd일 경우의 statement 이다. (뒤에 이어지는 statement 는 pd 이므로 구별하자.)
• SDT 로 분해한 결과의 square root를 확인할 수 있다는 것이다.
• 이때 람다는 A를 따라 nonnegative 다.
• 전개는 람다를 각각 1/2 승으로 쪼개고 또다시 이 사이에 Identity matrix 를 끼워넣는다.
• 그러면 A의 1/2 승을 또다시 정의할 수 있게된다, 가 요지이다. 이때 유심히 보면, eigenvectors 감마는 1/2승 후에도 변함이 없고, eigenvalues 만 1/2 승 된 것을 확인할 수 있다. (나중에 확인하면 알겠지만 이 diagonal lambda matrix 는 A가 몇 승인지를 따라간다, 로 일반화할 수 있다.)
• 아래는 A가 pd일 경우에 확장이다. 물론 지금 statement 는 pd일 경우에도 유효하고, 아래 주장이 추가로 가능하다.

Furthermore, if $\mathbf{A}$ is positive definite, we can define $\mathbf{A}^{-1 / 2}$. Note each $\lambda_{i}$ 's are nonnegative. Define $\Lambda^{-1 / 2}:= diagonal(각 람다의 -1/2 승)$
. Then,

• A가 pd일 경우엔 람다의 bound 도 positive 까지 올라오게 되고,
• A의 -1/2 승도 다음과 같이 정리할 수 있게 된다.
• 약간의 오탈자가 있지만 (끝에 SDT의 감마 가운데에 A가 아니라 역시나 계속해서 람다의 -1/2승이다) A의 거듭제곱을 람다가 따라가는 것을 확인할 수 있다.

계속 말한 일반화된 형태를 아래 statement로 정리하면, 끝!

• In general, for any positive definite $\mathbf{A}$ and a univariate polynomial function $\phi(\cdot), " \phi(\mathbf{A})$ " is defined by $\boldsymbol{\Gamma} \phi(\boldsymbol{\Lambda}) \boldsymbol{\Gamma}^{T}$ where $\phi(\boldsymbol{\Lambda}):=\operatorname{diag}\left(\phi\left(\lambda_{1}\right), \ldots, \phi\left(\lambda_{d}\right)\right)$.

phi polynomial function 이란 건 A에 지수로 어떤 것을 사용하든~ 이란 것으로 받아들이면 된다. 또 분해의 대상이 되는 A는 이제 확장하여 어느 positive definite 이든~ 으로 확장된다. (잠깐 뒤에 이걸 쓴다!) 이걸 람다의 diganal 각 component 들이 따라간다는 것. 실제로 이건 A의 지수로 유리수, 실수일 때도 가능하고, exp(A)나 log(A)의 형태도 가능하다. 아직은 사용하지 않겠지만..

이제 이어지는 다변량 정규분포의 내용을 보면, 앞서 언급한 것들이 하나씩 쓰일 것이다.

multivarate normal distribution

Definition 3.5.1. Let $\boldsymbol{\mu} \in \mathbb{R}^{d}$ and $\boldsymbol{\Sigma} \in \mathbb{R}^{d \times d}$ be a positive semidefinite matrix. Let

Then, the joint distribution of $\mathbf{X}$ is defined by multivariate normal distribution (다 변량 정규분포) with mean $\boldsymbol{\mu}$ and covariance matrix $\boldsymbol{\Sigma}$.

• 다변량 정규분포는 고정된 d차원벡터 뮤벡터와, psd matrix 시그마를 파라미터로 사용한다는 것. 사실 표준정규분포가 정규분포로 확장되었음을 똑같이 반복한 것인데, 이것이 d=1이 아닌 다차원으로 넘어오면서 벡터 또는 matrix 를 사용하게 되었다.. 로 이해하면 된다.

• 그러면 다변량 정규분포의 pdf 도 볼 것인데, 여기서 벡터 z(표준정규)에서 x(정규)로의 변환을 위해 Jacobian 을 사용하게 된다. (이전의 transformation 을 생각하면 된다.) 다만, 이 과정서 자연스럽게 covariance matrix 의 -1/2 승이 필요하기 때문에, pdf of X를 쓸 수 있다는 건 시그마가 positive definite 임을 가정한다, 필요로 한다 정도로 알아두자. (이 부분은 그렇게 필요한가? 싶긴 하다. 고개만 끄덕이면 될 듯.)

• The (joint) pdf of $\mathbf{X}$ exists when $\boldsymbol{\Sigma}$ is positive definite. From $\mathbf{x}=\boldsymbol{\Sigma}^{1 / 2} \mathbf{z}+\boldsymbol{\mu}$, we have $\mathbf{z}=\boldsymbol{\Sigma}^{-1 / 2}(\mathbf{xSss}-\boldsymbol{\mu})$ and

  $J=\left|\frac{d \mathbf{z}}{d \mathbf{x}}\right|=\left|\boldsymbol{\Sigma}^{-1 / 2}\right|=|\boldsymbol{\Sigma}|^{-1 / 2}$

So, the pdf of $\mathbf{X}$ is

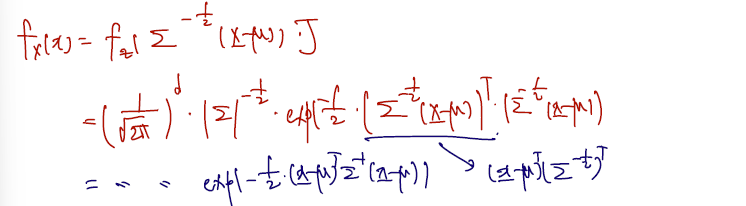
• 이정도 pdf 는 손에 익게 해두면 좋겠다.
• 다변량 표준정규분포의 pdf 와 다를 것이 없고.. 기존 z transpose z로 쓰였던 부분이 표준정규분포에서 정규분포로 넘어옴에 따라 뮤와 matrix 를 포함하게 되었다, 의 차이가 있다.
• 참, 다변량정규분포를 줄여서 MVN이라 부르기도 한다.

그렇다면 이 pdf of MVN의 contour plot 은 어떨까? contour plot 이란 건 f(x) = c 로 함숫값이 같은 x들을 하나의 선으로 연결해둔 것이다. 등고선도라고 하는데, 우리가 알고 있는 normal distribution 의 그림이 마치 축이 하나만 있는 종모양이라고 한다면 이를 다차원으로 확장한 그림은 어떨까, 하는 것이다. 역시나 마찬가지로 볼록한 지점과 그렇지 않은 지점이 나타날 것이다. 이에 대한 계산은 다음과 같이 한다.

(MVN의 pdf, mgf 외에 contour plot) How does the contour plot of $f_{\mathbf{X}}(\mathrm{x})$ look like?

Since $f_{\mathbf{X}}(\mathbf{x})=c \Longleftrightarrow(\mathbf{x}-\boldsymbol{\mu})^{T} \mathbf{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})=c^{\prime}$,
it suffices to imagine the contour plot of $\mathrm{x} \rightarrow(\mathrm{x}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\mathrm{x}-\boldsymbol{\mu})$.

• 일단 마지막 form 부터 보자. 우리의 목표는 pdf 를 무언가의 제곱 형태로 만드는 것인데, 이렇게 만드는 이유가 왼쪽에 보이듯 변수의 제곱들이 합해진 형태 (=자기자신 transpose 벡터끼리의 내적) 의 square root가 자취의 방정식의 그것과 일치하기 때문이다. 다시말해 이렇게 정리할 수 있으면, 이를 따르는 원을 그릴 수 있다. (선후관계는 분명하지 않다. pdf 를 정리했더니 이 form 이어서 원을 이쁘게 그릴 수 있었다, 가 좀 더 맞는 방향이겠다.)

• 여기서는 아까 썼던 스펙트럴분해정리를 쓸 수 있다. 시그마가 positive definite 이고, 그랬을 경우엔 분해된 람다에서 음수승도 자유롭게 쓸 수 있다고 했다. 그래서 람다의 -1승이든, -1/2 승이든 쓸 수 있게 된 것이다. 결국 최종형태에도 남아있다.

• 이제 기하학적 의미를 좀 살펴보면..
  

• 정확히 원을 그리는 g(x) 의 x 자리에 차래로 람다의 -1/2 x 를 대입하고, 감마x, x-뮤를 대입한 형태로 생각해볼 수 있다.

• 각 형태에 매칭되는 기하학적 contour plot 의 변화는 오른쪽에 있다. 1, 1, -1, -1 에서 출발한 원이,

• 첫 번째 eigenvalues 의 대입에선 그 값만큼 x, y좌표로 확장한다. (eigenvalues 이동)

• 두 번째 eigenvector 대입에선 예컨대 감마1, 감마2 의 square root 축을 따라 contour plot 의 원이 회전할 것이다. 이를 다차원으로 확장한다고 생각해주자. (eigenvectors 회전)

• 마지막으론 뮤의 좌표만큼 평행이동한다고 생각하자. 람다나 뮤나 정확히 dxd matrix 에서 나왔으므로 d차원까지 요소들이 존재하고, 따라서 d차원에 정확히 대응되는 뮤의 좌표가 있을 것이다. 이 지점을 마치 (0,0)처럼 쓰면 된다.

• 그럼 이제 다 왔다. 일변량 정규분포를 오른쪽 다변량 정규분포처럼 일반화할 수 있는 것!

(joint) mgf of X is

Properties of the MVN (3가지)

그런데 MVN은 정의나 pdf, mgf, contour plot 외에도 잘 알려진 named 분포에다가 성질 몇가지도 갖추고 있다. 아래의 성질들은 한 번 제대로 정의해두고 손에 익혀두면 매우 유용하게 쓰일 것이니까 잘 배워두자. 일부러 Theorem 번호도 살렸다!

Theorem 3.5.1 (Relationship with $\chi^{2}$-distribution). If $\mathbf{X} \sim N_{d}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$, then $\mathbf{W}:=$ $(\mathbf{X}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\mathbf{X}-\boldsymbol{\mu})$ follows $\chi^{2}(d)$.

• 첫번째로는 1차원에서 표준정규분포를 따르는 변수들의 제곱이 카이제곱(1)을 따랐던 것처럼, 다차원에서도 이를 일반화할 수 있다는 것이다.
• Z가 아닌 X가 다변량 정규분포를 따른다고 가정하는 것이 일반화해서 보여주기에 더 적합해서 이런 식을 생각한 것 같고, 이번엔 카이제곱 1이 아닌 확률변수 수이자 차원 수인 카이제곱 d를 따른다.
• 식이 복잡해보이지만 하나의 변수를 제곱해둔 형태일 뿐이다. 그리고 다차원이기 때문에 이를 transpose 하고.. 공분산 matrix 를 끼워넣느라 길어졌을 뿐인데, 변수가 다변량에서 일반화되면 이런 form 이구나, 여기서 챙겨두면 된다.

Proof. By definition of MVN, $\mathbf{Z}:=\boldsymbol{\Sigma}^{-1 / 2}(\mathbf{X}-\boldsymbol{\mu}) \sim N_{d}\left(\mathbf{0}, \mathbf{I}_{d}\right)$. So, $\mathbf{W}=$ $\mathbf{Z}^{T} \mathbf{Z}=\sum_{i=1}^{d} z_{i}^{2} \sim \chi^{2}(d)$

• 증명은 by definition 으로 z가 다변량 표준 정규분포를 따를 때, 이 z의 제곱이 카이제곱 d를 따름을 보여주면 된다. 변수 제곱의 합이 카이제곱 d인 건, 이미 일변량에서 알려진 사실이므로..
• 흥미로운 건 다변량 확장에선 이미 벡터 내적으로 정의가 될 수밖에 없기 때문에 (서로 다른 변수를 가정할 수 밖에 없으므로) 카이제곱 1을 쓸 순 없다는 것. -> 일변량에선 그 자체의 제곱은 카이제곱1, 이들의 합은 카이제곱 n을 따랐던 것과는 차이가 있다.

작성 중.. 아직 다 적진 않았고, 2.번은 linear transform 이 가능하다는 것, 3.은 공분산이 0이라면 독립이라는 것이 MVN 가정에서는 가능하다는 것. 이 있다.

이어서 MVN을 따르는 벡터 x가 적절히 선형변환 후에도 또다시 MVN을 따른다는 성질이다. 잘 알려진 분포라면 확률변수의 선형 변환 후에도 그 분포를 따른다는 것이 일반적이긴하다. MVN도 그렇다는 것! 아래를 보자.

Theorem 3.5.2 (MVN preserved under linear transform). Assume $\mathbf{X} \sim N_{d}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$. If $\mathbf{A} \in \mathbb{R}^{p \times d}$ and $\mathbf{b} \in \mathbb{R}^{p}$ are deterministic matrix and vector, then $\mathbf{Y}=\mathbf{A X}+\mathbf{b} \sim$ $N_{p}\left(\mathbf{A} \boldsymbol{\mu}+\mathbf{b}, \mathbf{A} \boldsymbol{\Sigma} \mathbf{A}^{T}\right)$.

• d차원 다변량 정규분포를 따르는 X가 있다고 할 때, 여기에 적절히 p x d 의 M matrix 를 곱하고 b vector 를 더하는 선형변환으로 Y라는 새로운 변수를 만들었다고 하자.
• 선형변환 후 Y에서도 여전히 MVN은 유지된다.
• 평균은 뮤로부터 선형 변환 한 만큼 움직이며, 분산 또한 A matrix 가 자기 자신과 transpose 가 앞뒤로 붙은 형태로 바뀐다.
• 이에 대한 증명은 mgf 를 이용하면 쉽게 할 수 있다. -> 생각보단 길다. mgf of Y에서 시작해서 X로, Z로 내려서 비교해야 하기 때문이다. 그런데 한 번 과정을 거치면 transpose 나 행렬 연산에 대한 기초체력이 길러질듯! 이미 한 번 해봤지만 나중에 다시 해볼 가치가 있는 것 같다.

3.5.2 해당 정리를 이용해 끼워팔기로 증명할 수 있는 게 하나있다. 전체 X random vector 을 X1, X2 로 쪼갠다고 했을 때, 이들의 jointly 하게 묶은 X가 normal 이라면 각각이 marginally 하게 normal 이라는 것인데.. 증명 호흡이 길지만 아래와 같다.

Corollary 3.5.1 (Marginal of MVN is also MVN). Suppose that $\mathbf{X} \sim N_{d}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$. Then, $\mathbf{X}_{1} \sim N_{p}\left(\boldsymbol{\mu}_{1}, \boldsymbol{\Sigma}_{11}\right)$ and $\mathbf{X}_{2} \sim N_{q}\left(\boldsymbol{\mu}_{2}, \boldsymbol{\Sigma}_{22}\right)$

Proof.

이를 위해 일단 필요한 가정은 다음과 같았다. (서술을 위해 순서를 좀 바꿨다.)
Assume that $\mathbf{X} \in \mathbb{R}^{d}$ is a random vector and partition $\mathbf{X}$ so that

where $\mathbf{X}_{1}$ is $p$-dimensional and $\mathbf{X}_{2}$ are $q$-dimensional $(p+q=d)$.

• d 길이짜리 random vector 을 X1, X2 각각으로 길이 p, q 만큼 잘랐다고 상상하자.
• 그리고 이들 사이의 모평균과 모분산, 공분산이 있다고 가정하자.
• 그럼 다음과 같이 증명할 수 있다.

• 첫 과정은 A라는 p x d 행렬을 정의하는 일이다. 이때 행렬의 왼쪽으로는 p x p가 되도록, 오른쪽으로는 p x (d-p) 길이가 되도록 하고, 왼쪽엔 Identity matrix 로, 오른쪽엔 0으로 구성한다.
• 그러면 random vector X를 A와 곱할 수 있게 된다. 많은 생각을 거치지 않아도 잘 정의된 길이 덕분에 X1이 튀어나온다는 것을 알 수 있고..
• 결국엔 X1 을 X의 선형변환을 통해 얻을 수 있다는 결론이 얻어진다. 앞서 theorem 2에서 논의했던 것은? 어떤 변수 X가 normal 이라면, 선형변환을 통해 얻은 새로운 확률변수도 normal 이라는 것. 같은 논리를 여기에도 적용하면 X1도 normal 을 따른다.
• 그럼 parameter 가 왜 matrix A가 빠진 form인지 의문을 품을 수 있으 건데, 잘 정의한 A를 넣어 계산해보면 실제로 뮤1과 공분산행렬 중 시그마11만 튀어나오는 것이 어려운 계산을 거치지 않아도 확인 가능하다.

Applying Theorem 3.5.2 leads to $\mathbf{X}_{1} \sim N_{p}\left(\boldsymbol{\mu}_{1}, \boldsymbol{\Sigma}_{11}\right)$. Similarly we can show $\mathbf{X}_{2} \sim N_{q}\left(\boldsymbol{\mu}_{2}, \boldsymbol{\Sigma}_{22}\right)$

마지막 성질을 보자.
Theorem 3.5.3 (zero correlation implies independence under MVN).
Suppose that $\mathbf{X} \sim N_{d}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$. Then $\mathbf{X}_{1}$ and $\mathbf{X}_{2}$ are independent if and only if $\boldsymbol{\Sigma}_{12}=\mathbf{O}$.

이전부터 두 변수 X1 과 X2 가 독립일 때 이들의 공분산은 0임을 의미한다고 배웠고 그 fact 를 다양한 계산에 자유롭게 사용해왔다. 그런데 이건 trivial 한 사실이고.. MVN에선 공분산이 0이라는 것이 독립임을 확정 짓는데 충분조건이 된다는 non-trivial 이 가능하다.

이에 대한 증명은 mgf를 이용할 것이다. 사실 독립임을 증명하는덴 3가지가 가능했었다. 각각의 joint pdf 가 marginal pdf 의 곱과 같거나, cdf가 그렇거나, mgf에서 그렇거나. 여기선 mgf 를 이용하여 joint mgf 를 쓰고, 계산 시 if 공분산 =0 을 끼워넣었을 때 각 margianl mgf 의 곱이 튀어나오는지 확인하면 된다.

• 공분산의 각 요소들을 쓰고, cross 에 해당하는 것들을 날리면 된다.
• 오탈자가 있어보인다. 각 exp 은 더하기가 아닌 곱으로 연결되고,
• 따라서 최종 form 도 mgf 의 덧셈이 아닌 marginal mgf 의 곱이 jointly mgf 가 된다는 사실을 보이면 된다.

성질 3개는 다 지나갔지만.. 잘 정의된 분포가 자주 따르는 additivity 도 MVN이 따름을 챙겨두자.
Theorem (Additivity of the MVN). If $\mathbf{X}_{1} \sim N_{d}\left(\boldsymbol{\mu}_{1}, \boldsymbol{\Sigma}_{1}\right), \mathbf{X}_{2} \sim N_{d}\left(\boldsymbol{\mu}_{2}, \boldsymbol{\Sigma}_{2}\right)$ and $\mathbf{X}_{1} \perp \mathbf{X}_{2}$, then

각각이 독립이고 normal 을 따르는 변수 X1과 X2를 하나로 묶어 joint pdf of X로 정의하는 것도 가능하고 / 이들을 단순히 더했을 때 역시나 normal 을 따른다는 것! 이에 대한 증명 역시 3.5.2 를 통해 mgf 로 할 수 있다.

(1)

(2) $\mathbf{X}_{1}+\mathbf{X}_{2} \sim N_{d}\left(\boldsymbol{\mu}_{1}+\boldsymbol{\mu}_{2}, \boldsymbol{\Sigma}_{1}+\boldsymbol{\Sigma}_{2}\right)$

소감

앞 1, 2, 3 장에서 가장 잘 알려져있고 중요한 내용을 꼽으라면 여기가 될 것 같다. normal distribution 이 잘 알려진 분포일 뿐더러 다변량으로 확장된 일반적인 form 이기 때문인 것 같다. 모든 흐름이 집약되어 있는 느낌이고.. 내용이 많지만 각각을 입체적으로 보면 얻을 수 있는 fact 들이 많다. 여기서는 계산상의 증명뿐 아니라 이어지는 성질들이나 이를 직관적으로 이해할 수 있는 방법론들까지 모두 챙겨두는 게 맞는 것 같다라는 생각이 든다.

하나 궁금증이 드는 건.. jointly MVN을 따를 때 각 확률변수 X1, X2가 marginally normal 을 따르는 건 증명이 되었지만, 역이 가능한가? 적절하게 증명이 되는가? 에 대한 의문이 들었다. margianlly normal 일 때 jointly normal 인 상황은 바로 위 1에서 다루고 있지만.. (둘이 indep인 경우) 이게 적절한 증명은 아닌 거 같고, 식으로 잘 풀 방법이 있나 고민이다. 곧 다시 언급될 것이니 돌아와야지.

아무튼, 오랜만에 즐거웠다!🤗