[Mathematical Statistics] 3.6 t- and F- distributions

이 장에서는 t분포와 F분포의 정의, 스튜던트 정리에 대해 다룰 것이다. 특히 스튜던트 정리는 statement 나 이를 증명하는 과정이 통계쪽으로 넘어가는데 이어지는 느낌이므로, 잘 기억해두자. 시작하자!

3.6 t- and F- distributions

1. t-distributions

t분포와 F분포는 깊은 성질로 들어가기 보다 정의만 잘 챙겨두자. 정의는 다음과 같다.

Definition

필기가 약간 흩으러지긴 했는데.. 내용은 이렇다.

• 분자는 표준정규분포를 따르고
• 분모는 카이제곱(r)에 자유도 r로 나눈의 square root. (r>0)
• 그리고 표준정규분포를 따르는 W와, 카이제곱을 따르는 V가 independence 일 때
• 이렇게 구성한 변수가 따르는 분포를 t분포라고 한다.

이렇게 표시한 t분포의 parameter 는 자유도 r이다. 따라서 다음과 같이 쓴다.

then the random variable $T$ is called to have a t-distribution with degree of freedom $r$ (자유도 $r$ 의 $t$-분포).

pdf
t분포의 pdf 는 다음과 같이 쓰는데, 이걸 외우기보단 정규분포와 살짝 비교하면..

이걸 다 외우기보단 변수 t에 depend 하는 term 만 써보자. 그럼 t의 -(r+1)승이 되는데, 정규분포가 exp(-t^2/2) 였던 것과 비교하면.. t분포는 유 비교하면.. t분포는 유리함수고 정규분포는 지수함수이니 t가 무한대 꼬리쪽으로 갈수록 더 늦게 떨어지는 것은 t분포쪽이다. 그림을 보자.

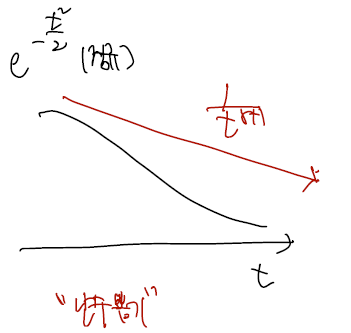
• 이러한 성질 때문에 난수뽑기와 같은 문제가 있을 때 정규분포 대신 t분포를 선택하면, 0으로부터 멀리 떨어진 난수를 효과적으로 뽑을 수 있게 된다.
• 만약 r=1을 집어넣으면 t의 -2승이고,
• r=3 을 집어넣으면 t-4승이니.. 자유도가 커질수록 0으로 빠르게 붙게될 것이다.
• 그런 이유 때문에 자유도란 이름을 썼지 않나 싶다.

2. $F$-distribution

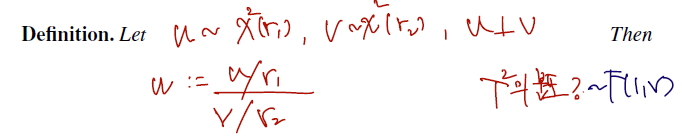
이것 역시 필기가 온전치 못하나, 읽어보면

• 카이제곱 r1을 따르는 u와, 카이제곱 r2를 따르는 변수 v가 있고, 이 둘은 독립이라 하자.
• 그때 분자엔 u를 자유도 r1으로 나눈 것, 분모엔 v를 r2로 나눈 것으로 새로운 변수를 구성하면, 이 변수가 따르는 분포는 $F$-distribution 이라 이름 붙인 것이다.
• 따라서 $F$-분포는 para r1,r2를 가진다. 다음과 같이 쓴다.

F-distribution with degrees of freedom $r_{1}$ and $r_{2}$ (자유도가 $\left(r_{1}, r_{2}\right)$ 인 $F$-분포.

• The pdf of $W$.

• 여기서 한가지 fact 는 T제곱의 분포가 따르는 것이 F(1,r)이란 것이다. 증명은 아래와 같다.
  

3. Student's theorem
다음으로 알아볼 것은 스튜던트 정리이다. 스튜던트 정리는 a~d까지 4가지 핵심적인 statement 들을 포함하는데, 증명으로 넘어가기 전 우선 어떤 주장들인지 먼저 보자.

Theorem 3.6.1 (Student's theorem). Let random variables $X_{1}, \cdots, X_{n}$ are iid from $N\left(\mu, \sigma^{2}\right)$. Define $\bar{X}:=\frac{1}{n} \sum_{i=1}^{n} X_{i}$ and $S^{2}:=\frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}$. Then,
(a) $\bar{X} \sim N\left(\mu, \sigma^{2} / n\right)$;
(b) $\bar{X}$ and $S^{2}$ are independent;
(c) $\frac{(n-1) S^{2}}{\sigma^{2}} \sim \chi^{2}(n-1)$; and
(d) $\frac{\bar{X}-\mu}{S / \sqrt{n}} \sim t(n-1)$.

• 정규분포에서 iid 로 뽑은 X1.. Xn이 있다고 하고, 이들의 표본평균과 표본분산을 각각 정의하였다.
• 이제 a부터 d까지 하나씩 증명할 것이다. a부터 c까지가 약간의 독립적인 증명이고, 이걸 이용해서 d를 증명해내는 구조.

a 의 증명

• X의 표본평균이 모평균 뮤와 시그마제곱을 n으로 나눈 분산을 따르는 normal 을 따른다는 증명이다.
• 각각의 변수 Xi(실제 값들)가 margianlly normal 이고, indep이므로 jointly normal인 fact 는 바로 앞장에서 배웠고..
• 그래서 이들을 모은 vector X가 따르는 분포도 생각해낼 수 있다. 간단히 뮤는 vector 이므로 뒤에 1n을 써줬고, 시그마 제곱은 더이상 스칼라 값이 아닌 행렬이므로 nxn identity matrix 를 붙여줬다.
• 정의에 따라 표본평균을 실제 값들의 벡터 X를 포함한 벡터 내적으로 쓸 수 있다.
• 따라서 표본평균은 실제 값들을 모아둔 vector X의 선형변환이고, 이 vector X가 이미 normal 을 따르고 있으니.. 표본평균도 normal 을 따르게 된다.
• 재미있는 건, 후에 통계량에 대한 이야기에서도 언급되겠지만 이런 성질, 추정량인 v표본평균이 normal 을 따르고 이들의 expectation 이 모평균을 따른다 (비편향성) 이런 것들이 '잘 정의된' 모수들의 특징이다. 다음장에서 이 이야기를 하도록 하자.
• 굳이 이 표본평균이 왜 뮤와 시그마제곱/n을 parameter 로 하는지는 아는 것을 그대로 써도 되고, 한 번 계산을 거쳐도 된다.

b의 증명

(1)

(2)

c의 증명

(1)

(2)

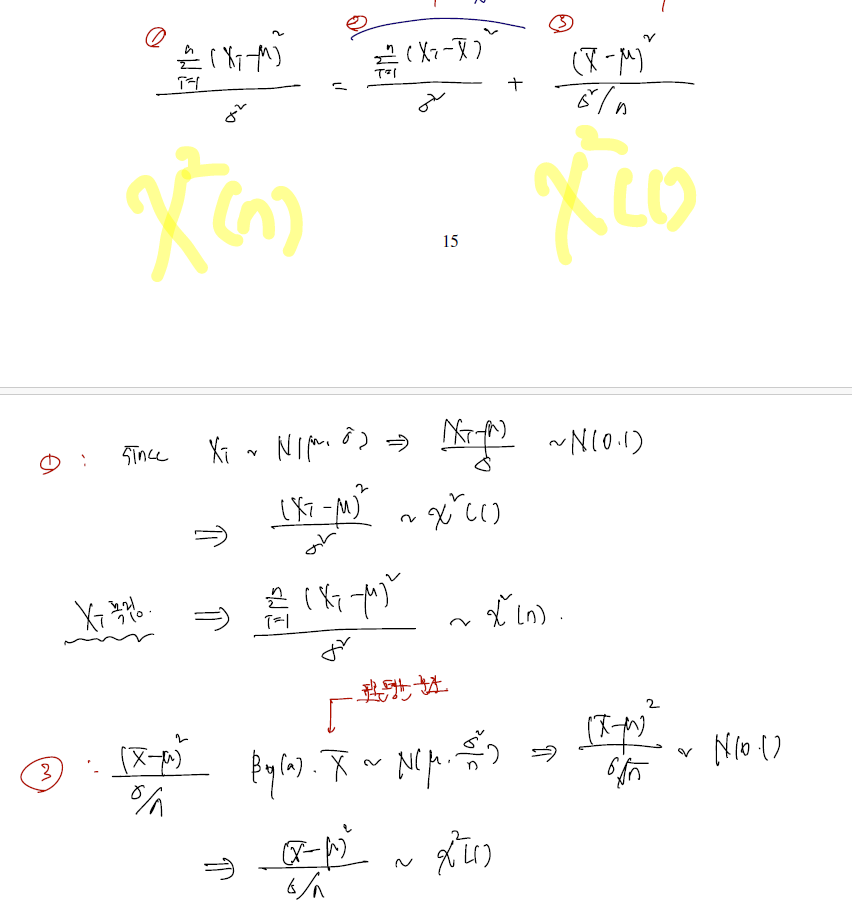
(3)

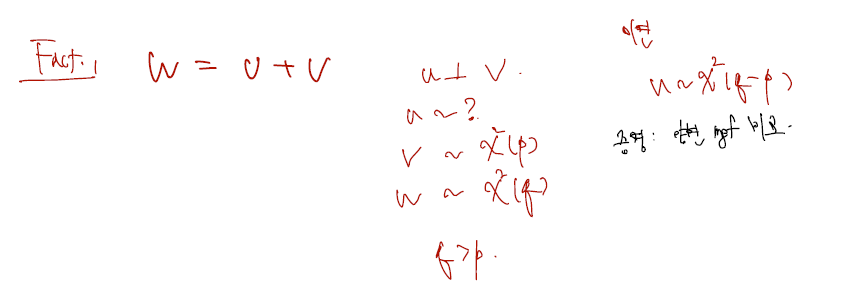
d의 증명