[Mathematical Statistics] 3.3 Gamma, chi, beta Distributions | 3.4 The normal distributions

박경민·2024년 9월 17일

[Mathematical Statistics]

목록 보기

8/24

Recall

이전까지 했던 분포들을 간단히 review 해보자.

베르누이의 support 는 0 또는 1, Poisson 분포의 support 는 0을 포함한 모든 실수였다. pmf 는 써둔 것과 같고.. 각각 베르누이에서는 모수 p (사건이 일어날 확률)이 평균과 분산을 결정하고, 포아송 분포에서 역시 이와 비슷한 람다 (E(x)와 같다.) 가 평균과 분산이 되어준다는 것. 포아송에서는 평균과 분산 값이 람다로 같았다는 것 정도를 기억하면 되겠다.

베르누이와 포아송을 말로 풀어 설명하면 어떤가? 베르누이 분포는 성공확률이 p로 동일한 실험을 반복할 때, 성공횟수 (또는 k번 성공하기까지 시행횟수) X에 대한 분포이다. 포아송 분포는 정해진 길이, 연속된 구간이 주어질 때 그 사이에서 사건이 몇 회 일어날 지 횟수 X에 대한 분포이다. 앞으로 다룰 감마분포는, 특정 사건이 K번 일어나기까지 걸리는 시간 / lenght 수에 대한 분포이다.

감마 분포를 알기 위해선 우선 감마함수부터 살펴보고 넘어가야 한다.

\Gamma(\alpha):=\int_{0}^{\infty} y^{\alpha-1} e^{-y} d y, \quad \alpha>0

일단 복잡한 의미를 생각하지 않고, properties 와 이를 활용한 감마 분포로 넘어가도록 하자. 참고하자면 아래 다음과 같이 양변을 $\Gamma(\alpha)$ 로 나눈 식을 사용할 것이다.

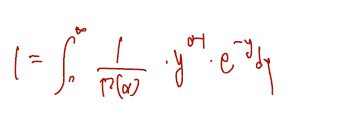
Properties

\begin{aligned} \Gamma(1) & =1 \\ \Gamma(\alpha) & =(\alpha-1) \Gamma(\alpha-1), \quad \text { for any } \alpha>1 \\ \Gamma(n) & =(n-1)!, \quad \text { for any integer } n \geq 2 \\ \Gamma(1 / 2) & =\sqrt{\pi} \end{aligned}

첫번째와 마지막 감마분포에 1, 1/2 을 대입한 값은 그냥 외워두자. 하나 중요한 것은 감마분포가 !(팩토리얼)의 일반화라는 점. 두번째와 세번째 특징에서 유도 가능하다. 다음으론 감마 분포.

Definition (Gamma distribution)

감마분포는 파라미터 알파, 베타 > 0일 때를 모수로 다음과 같은 pdf 를 취한다.

f(x)=\frac{1}{\Gamma(\alpha) \beta^{\alpha}} x^{\alpha-1} e^{-\frac{x}{\beta}}, \quad x>0

pdf를 validate 하기 위해 다음을 쓴다.

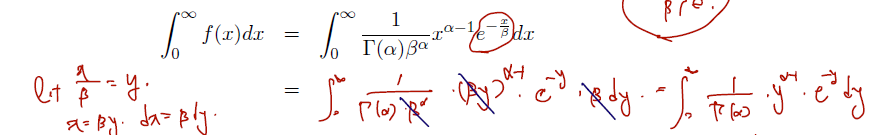
마지막 식은 위에서 gamma function 을 확인할 때 이미 봤던 식이므로, 이 식의 적분 값은 1임을 확인할 수 있다.

감마분포는 poisson process 의 세 공리 (이후에 정리할 것이다.)를 따르는 사건이 K회 발생하기까지 걸리는 기간이다. 여기서 유도를 다루진 않을 것이나.. 다음과 같은 곳에서 사용됨을 알아두자. -> 수명, 서비스시간, 고장시간 모델링.

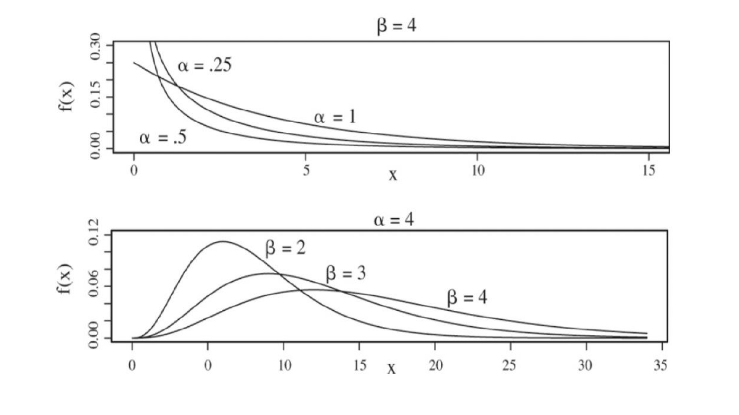
감마분포의 모수가 되는 알파는 shape 파라미터, 베타는 scale 파라미터라 불린다. 특히 감마분포 pdf 는 exponential 함수에 depend 하는 베타에 영향을 많이 받는데, 베타 값이 커질수록 그래프를 양옆으로 찢는 형태가 되며, 이를 x에 붙어 scale 을 조절한다 하여 scale 파라미터라 부른다.

mgf of $\operatorname{Gamma}(\alpha, \beta)$ . If $X \sim \Gamma(\alpha, \beta)$ , then we have

감마 분포의 정의는 x 0부터 무한대까지이므로 이를 감안해서 적분을 쓰고
유도 과정 중 exponential 위의 파트를 치환하는 것만 잘 해내면 그 이후로 문제가 없다.
다만 치환 과정에서 t에 대한 범위가 생기므로 이를 잘 챙겨두자.

Then, we have

\begin{aligned} M_{X}^{\prime}(t) & =\frac{\alpha \beta}{(1-\beta t)^{\alpha+1}} \\ M_{X}^{\prime \prime}(t) & =\frac{\alpha(\alpha+1) \beta^{2}}{(1-\beta t)^{\alpha+2}} \end{aligned}

Therefore,

\begin{aligned} \mu & =E(X)=M_{X}^{\prime}(0)=\alpha \beta \\ \sigma^{2} & =\operatorname{Var}(X)=M_{X}^{\prime \prime}(0)-\mu^{2}=\alpha(\alpha+1) \beta^{2}-(\alpha \beta)^{2}=\alpha \beta^{2} \end{aligned}

감마분포의 평균은 parameter 의 곱, 분산은 베타가 한 번 더 곱해진 형태라는 것만 기억해두자.

이제 감마분포와 유사하게 생긴 다른 분포들을 살펴보자.

1. The exponential distribution
임의의 변수 X에 대해 exponential 분포는 다음과 같다.

f(x)=\frac{1}{\beta} e^{-\frac{x}{\beta}}, \quad x>0

감마분포에서, x에 depend 하는 항만 적어보면 다음과 같으니 지수분포는 감마분포와 닮아있다고 할 수 있고, $\Gamma(1, \beta)$ 과 같다고도 표현할 수 있다.

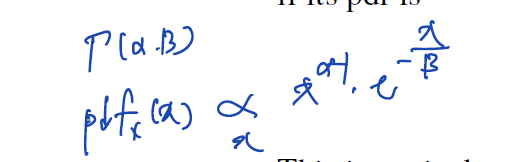
따라서 $\Gamma(1, \beta)$ 의 형태로 쓴다면 mgf나, 평균 분산을 아래와 같이 쓸 수 있다.

\begin{aligned} M_{X}(t) & =\frac{1}{1-\beta t}, \quad t<1 / \beta \\ E(X) & =\beta \\ \operatorname{Var}(X) & =\beta^{2} \end{aligned}

2. The chi-square $\left(\chi^{2}\right)$ distribution

카이제곱분포는 $\Gamma(2/r, \beta)$ 의 형태로 정의된 다음의 pdf 를 따른다.

f(x)=\frac{1}{2^{r / 2} \Gamma(r / 2)} e^{-\frac{x}{2}} x^{\frac{r}{2}-1}, \quad x>0

따라서 아래의 것들도 얻을 수 있다.

\begin{aligned} M_{X}(t) & =\frac{1}{(1-2 t)^{r / 2}}, \quad t<1 / 2 \\ E(X) & =r \\ \operatorname{Var}(X) & =2 r \end{aligned}

카이제곱 분포가 알려진 분포인 건, X를 N(0,1) 을 따르는 변수라 할 때 이들의 제곱의 분포가 카이제곱(1)의 분포를 따르기 때문이다. (아래 그림에서 쓰임 1.) 또한, X1부터 Xr까지 각각 i.i.d 하게 N(0,1)을 따르는 변수들의 합은 카이제곱(r)의 분포를 따른다. 이때의 카이제곱 parameter는 더해진 분포의 개수, r개로 정해진다.

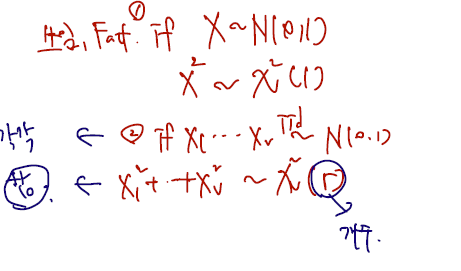
쓰임 1과 2 사이는 가법성을 통해 쉽게 증명이 가능하다. X가 알파가 고정되어있지 않고 제각각인 (베타는 고정) 감마분포에서 가져올 때, 이들의 합 Y는 또다시 감마분포를 따르면서 알파를 그대로 더한 값을 또다시 parameter 갖는다는 것. 아까 1.에서도 제곱한 변수들이 $\Gamma(1/2, 2)$ -> 카이제곱을 따른다고 했을 때, 이들을 더한 Y의 분포가 있다면 그건 $\Gamma(r/2, 2)$ 가 된다는 것이다! 이런 가법성에 대한 증명을 보자.

Theorem 3.3.1 (Additivity).
Let $X_{i} \stackrel{\text { ind }}{\sim} \Gamma\left(\alpha_{i}, \beta\right)$ , 그러면 다음과 같다.

Y=\sum_{i=1}^{n} X_{i} \sim \Gamma\left(\sum_{i=1}^{n} \alpha_{i}, \beta\right)

Y=\sum_{i=1}^{n} X_{i} \sim \Gamma\left(\sum_{i=1}^{n} \alpha_{i}, \beta\right)

(pf): mgf 를 통한 증명.

일반적인 감마함수의 mgf 처럼 보이지만 사실은 Y에서의 정의는 이것들이 서로 곱해져 지수쪽으로 간다.
그러면 감마함수 내에서 parameter 가 알파만 더해진 형태로 표현될 수 있는 것.
따라서, mgf 의 Y가 사실은 x의 합으로 표시되고, 이 형태가 감마함수에서도 남아있음을 보이면 된다.

추가로 다음도 보일 수 있다. 이는 카이제곱 r이 각각 r/2, 2 를 모수로 하는 감마분포를 따르고, 이것들을 더하면 r에 대해서만 시그마를 씌워주면 되므로 아래와 같이 쓸 수 있는 것이다.

Corollary. Let $X_{i} \stackrel{\text { ind }}{\sim} \chi^{2}\left(r_{i}\right)$ for $i=1, \ldots, n$ . Then, we have

Y=\sum_{i=1}^{n} X_{i} \sim \chi^{2}\left(\sum_{i=1}^{n} r_{i}\right)

Example Let $X \sim \Gamma\left(\frac{r}{2}, \beta\right)$ and $Y=2 X / \beta$ for some positive integer $r$ and positive real number $\beta$ . Derive the distribution of $Y$ .

변환의 분포 구하기 문제이다. 여기서는 pdf 까지 갈 것 없이 mgf 만 이용해서 쓰면 된다. 이 문제는.. 조금 더 확장해서 다음의 문제로 바꾸자.

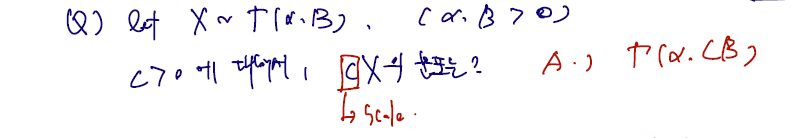
그러면 다음과 같이 풀 수 있다.

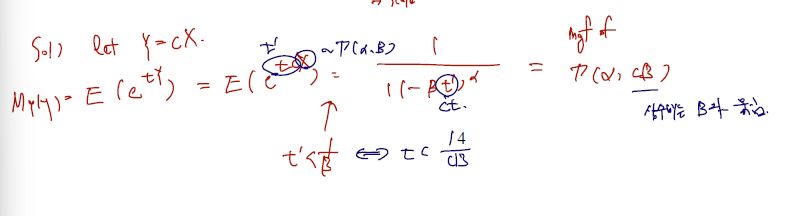
mgf 원래 식에 t대신 tc 를 scala 로 볼 수 있으므로 이 자리를 채운다고 하면, C는 scale parameter 베타와 묶인다. 이 문제역시 감마분포가 r/2, 2 를 모수로 하는 분포가 되는데 이건 카이제곱(r)의 분포와 같다. 따라서, 결론적으로 임의의 감마분포는 적당히 scale 변환 후 카이제곱분포로 변환이 가능함을 알 수 있다.

Beta distribution

베타분포는 다음과 같이 정의할 수 있다. 파라미터 알파, 베타 >0 가 있을 때, pdf 는 다음과 같다.

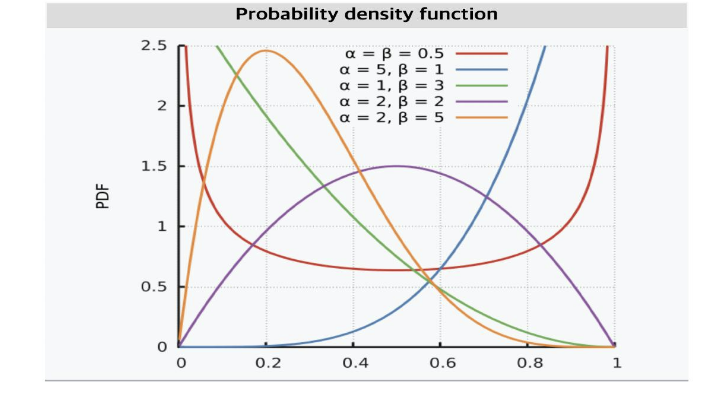
f(x)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1}, \quad 0<x<1

베타분포의 support 는 0, 1 사이의 실수임에 주의하자. 그래서 사건의 발생확률 자체를 모델링할 때 사용되기도 한다.
x에 대해 마치 다항함수와 같으므로 알파 베타 값에 따라 그래프가 다음과 같이 변한다.

🤔문제.

Relationship with the Gamma distribution.

Fact A. If $X_{1} \sim \Gamma(\alpha, 1), X_{2} \sim \Gamma(\beta, 1)$ and $X_{1} \perp X_{2}$ , then $Y=\frac{X_{1}}{X_{1}+X_{2}} \sim$ $\operatorname{Beta}(\alpha, \beta)$ .

각 감마분포가 주어질 때 이것들의 비율이 베타분포라는 증명인데, 아직 풀지 못했다ㅠ 얼른 풀어야지. joint pdf 도 쓰고, 거의 마지막 단에 다다른 거 같으나, 마지막 베타분포로 넘어가는 길을 찾지 못한 것 같다.

Mean and variance of $\operatorname{Bet} a(\alpha, \beta)$ : If $X \sim \operatorname{Bet} a(\alpha, \beta)$ ,

\begin{aligned} E(X) & =\frac{\alpha}{\alpha+\beta} \\ \operatorname{Var}(X) & =\frac{\alpha \beta}{(\alpha+\beta+1)(\alpha+\beta)^{2}} \end{aligned}

평균에 대한 pf 는 다음과 같다.

감마함수가 팩토리얼 성질을 지녔다는 걸 잘 쓰면 쉽게 증명이 가능하다.

The normal distribution

정규분포에 대해선 많이 아는 내용이므로 간략하게 정리하고 가자.

변수 Z가 다음의 pdf 를 따르는 것을 standard noraml distribution, 표준정규분포를 따른다고 한다.

f(z)=\frac{1}{\sqrt{2 \pi}} e^{-z^{2} / 2}, \quad z \in \mathbb{R}

표준정규분포는 표현하기 쉽게 $\phi(z)$ 라 적기도 한다. phi 함수는 모든 실수 z에 대하여 y축 대칭이다. We can see that $\phi(z)=\phi(-z)$
cdf 는 대문자로 다음과 같이 적는다. $\Phi(z):=P(Z \leq z)=\int_{-\infty}^{z} \phi(t) d t$

표준정규분포의 mgf + moments

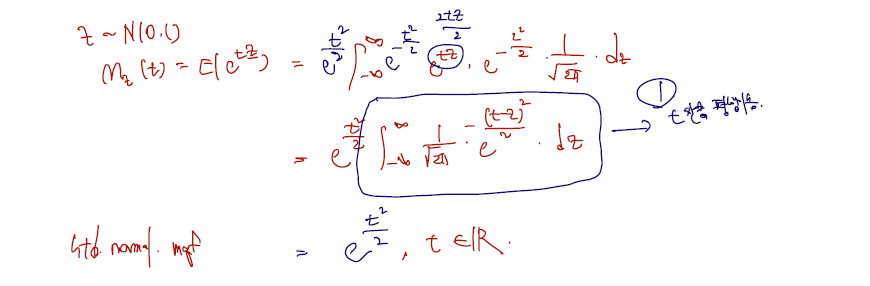
정규분포의 평균이 0이고 분산이 1이란 점은 잘 알려졌지만 계산에 의해서 다음과 같다.

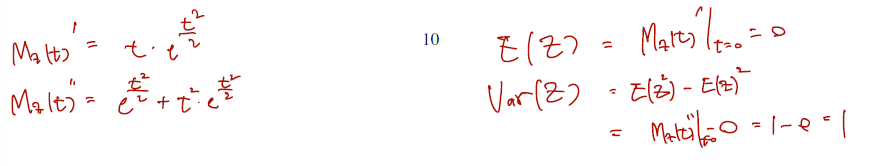
Normal distribution
이제 정규분포로 넘어와보자.

For $\mu \in \mathbb{R}$ and $\sigma>0$ , define a continuous random variable $X$ by $X=$ $\mu+\sigma Z$ , where $Z \sim N(0,1)$ .
pdf of X는 다음과 같다.
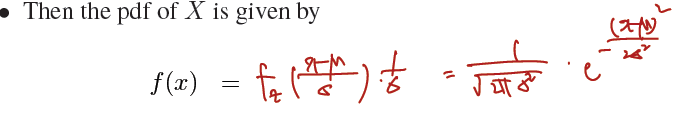
해석을 굳이 덧붙이면, std.normal pdf를 $\mu$ 만큼 평행이동하고 $\sigma$ 만큼 잡아당긴 것과 같다. 따라서 $X \sim N\left(\mu, \sigma^{2}\right)$ 와 같이 쓴다.

정규분포의 mgf

Theorem (Connection to the chi-square distribution).
If $X \sim N\left(\mu, \sigma^{2}\right)$ , then $W=(X-\mu)^{2} / \sigma^{2} \sim \chi^{2}(1)$ .

z가 표준정규분포 N(0,1) 을 따를 때 (=X가 정규분포를 따를 때) 왜 이들의 제곱은 카이제곱(1)를 따를까? 이에 대한 증명이다.

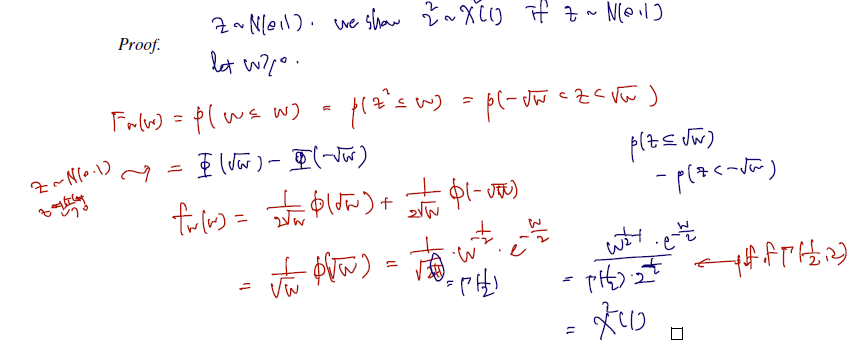
증명은 X 대신 표준정규분포를 따르는 Z로 하며, Z의 제곱이 카이제곱(1)을 따름을 보인다.
시작은 cdf of w로 한다.
미분해서 pdf of w로 넘어온다.
pdf of w가 카이제곱(1)과 같음이 증명되었다. w는 원래 z^2의 제곱과 같으므로 z^2이 카이제곱(1)과 같으을 보였다.

🤔 문제.

Theorem
Let $X_{i} \stackrel{\text { ind }}{\sim} N\left(\mu_{i}, \sigma_{i}^{2}\right)$ for $i=1, \ldots, n$ . Then, for any constants $a_{1}, \ldots, a_{n}$ ,