[Mathematical Statistics] 4. Elementary Statistical Inference

4.1 Sample and statistics

확률변수 X가 따르는 pdf 또는 pmf 를 하나의 함수라 할 때, 통계 문제는 다음과 같은 2가지 case 로 분류할 수 있다.

(1) $f(x)$ 가 전혀 알려지지 않았다. — "비모수적 문제" (nonparametric problem)
(2) $f(x)$ 의 형태는 알려져 있으나 ${ }^{1}$ 모수 $\theta$ 를 모른다 (여기서 $\theta$ 는 스칼라 또는 벡터일 수도 있다) — "모수적 문제" (parametric problem)

• 1) pdf 를 알지 못한 상태에서 X가 어떤 pdf 를 따르는지를 푸는 문제. 그런데 이건.. 클래스가 방대하고 따라서 문제의 난이도도 어려워 학부수준에선 잘 다루지 않는 것 같다.
• 2) 번의 케이스는 조금 다르다. pdf 또는 pmf 를 안다고 할 때, (여기서 안다고 하는 건 알려졌다고 가정하는 것이긴 하지만,) 이들이 가지는 모수를 추정하는 문제이다.
• 따라서 모수 추정이 목표이냐 아니냐에 따라 nonparametric, parametric 문제로 볼 수 있다.

앞서 다룬 몇가지 special distribution 을 예시로 2)가 고려하는 예시를 생각해볼 수 있다.

(a) $X$ 는 지수분포 $\operatorname{Exp}(\theta)$ 를 따르며, 여기서 $\theta$ 는 모른다.
(b) $X$ 는 이항분포 $B(n, p)$ 를 따르며, 여기서 $n$ 은 알지만 $p$ 는 모른 다.
(c) $X$ 는 감마분포 $\Gamma(\alpha, \beta)$ 를 따르며, $\alpha$ 와 $\beta$ 모두 모른다.
(d) $X$ 는 정규분포 $N\left(\mu, \sigma^{2}\right)$ 을 따르며, 여기서 $X$ 의 평균 $\mu$ 와 분산 $\sigma^{2}$ 을 모두 모른다.

이런 문제들은

• 모수(parameter), 즉 세타가 사는 세상을 모수공간이라 한다. 이에 대한 표기는 parameter space 를 다음과 같이 표현한다. $\theta \in \Omega$
• 위의 문제들을 formal 하게 표현하는 한 방법은 '$\mathbf{p d f} f(x ; \theta)$ 를 따른다' 이다.
• pdf는 $f_{\theta}(x), f(x \mid \theta), \operatorname{pdf}_{\theta}(x)$ 라고도 쓴다.
• 주어진 이 pdf 에서 세타값들은 고정된 값이다.
• 이 pdf 에서 X가 추출된다고 가정하는 것.
• 따라서 우리의 목표는 세타를 추정(estimate)하는 것이고, 이에 대한 정보는 X의 sample 로부터 얻는다.

Definition If $X_{1}, \ldots, X_{n}$ are iid (independent and identically distributed), such a set of random variables are called a random sample (확률표본).

• 여기서 표본의 관찰 개체는 X와 동일한 분포를 가지고, 확률변수 $X_{1}, X_{2}$, $\cdots, X_{n}$ 로 나타낸다.
• 항상은 아니지만 표본의 관찰개체를 iid 라고 가정 (독립이며 같은 분포에서 추출)하는 경우가 많고, 이런 경우 표본을 확률표본이라 부른다.

Definition function of the sample $X_{1}, \ldots, X_{n}, T=T\left(X_{1}, \ldots, X_{n}\right)$, is called a statistic (통계량). Once the sample is drawn with the realizations $x_{1}, \ldots, x_{n}$, $t=T\left(x_{1}, \ldots, x_{n}\right)$ is the realization (실현값) of the statistics.

• 표기에서 T는 n개의 Sample 주어졌을 때 output 으로 대응하는 규칙 자체를 말하며, 따라서 T는 통계량이 된다.
• 통계량의 예시는.. 표본평균, 표본분산, median, dxd 공분산 행렬 등 Sample 로부터 계산할 수 있는 것들이다.
• 표본이 실제로 추출되었을 때는 이들의 realization 이라 부르며 소문자$x_{1}, x_{2}, \cdots, x_{n}$ 으로 표기한다. 따라서 output 역시 t이다.

Definition. If $X_{1}, \ldots, X_{n}$ is a random sample with a pdf $f(x \mid \theta)$ where $\theta \in \Omega$ for some given set $\Omega$, then the statistic $T$ is an estimator (추정량) or point estimator (점추정량) of $\theta$. The realization $t$ of $T$ is an estimate (추정치) or point estimate (점추정치) of $\theta$.

• 분포의 모평균 뮤가 존재할 때, 표본평균은 통계량인 동시에 추정량이다. 이를 estimator 또는 point estimator 라 한다.
• 이에 실제로 채워지는 값은 추정치(estimate)라 한다. 따라서 추정량은 규칙, 추정치는 숫자, 정도로만.. 구별해두자.

Definition Let $X_{1}, \ldots, X_{n}$ denote a sample with pdf $f(x \mid \theta)$, where $\theta \in \Omega$. Then $T=T\left(X_{1}, \ldots, X_{n}\right)$ is an unbiased estimator (비편향추정량, $\boldsymbol{U E}$ ) of $\theta$ if

• 그렇다면 어떤 추정량, 예를들어 표본평균이 비편향추정량 UE라는 것은 무엇일까? 비편향추정량이란 것은 추정량이 그래도 믿을만한/쓸모있는 통계량이란 것인데, 이를 어떻게 말할 수 있을까?
• 모든 실제 세타의 paramter space에서, 추정량의 expectation 이 실제 모수를 따름을 보여주면 된다.
• 이미 아는 예시로, 우리는 $E(X)=\mu$ 일 때, 이 뮤를 가지는 pdf에서 iid로 추출된 random sample X1..Xn이 있다고 하자. 그러면 이들을 가지고 추정한 표본평균의 expectation 이 뮤와 같음을 보여주는 것, 했던 것이다!
• 또다른 예시는 그림으로.
  

이외에도 "좋은" 추정량 $\widehat{\theta}=T\left(X_{1}, \ldots, X_{n}\right)$ 의 미덕으론 다음 성질들이 있다.

• 비편향성(unbiasedness): $E(\widehat{\theta})=\theta$
• 일치성(consistency): $\widehat{\theta} \longrightarrow \theta$ as $n \rightarrow \infty$ (확률변수의 수렴의 정의는 5장에)
• 점근정규성(asymptotic normality): $\widehat{\theta} \approx N(\theta, \operatorname{Var}(\widehat{\theta})$ ) as $n \rightarrow \infty$ (기호 " $\approx "$ 의 사용이 허용되는 맥락도 5장에서 소개됨).
• 효율성(efficiency, minimal variance proporty): $\theta$ 의 임의의 비편향추정량 (또는 임의의 일치추정량) $\tilde{\theta}$ 에 대하여, $\operatorname{Var}(\widehat{\theta}) \leq \operatorname{Var}(\tilde{\theta})$.

약간의 설명을 덧붙이자면, 일치성은 sample 의 수가 커질 때 추정량이 모수로 수렴함 (대수의 법칙)을 말하고 있다. 점근정규성은 예측된 세타, 추정량이 실제 세타 주위에서 정규분포를 따름을 말하고 있고.. 효율성은 신뢰구간이 긴 것보다 잛은 추정량이 효율적이다라 말한다.

이제 분포, 분포의 모수에 대한 추정량을 construct 하는 방법 중 하나인 MLE를 알아보자. 참고로 추정량을 알아내는 방법들은 아래와 같이 더 있다. 이 중에서도 MLE 가 중요하다!

• Method-of-moment estimation (MME; 적률추정법)
• Maximum likelihood estimation (MLE; 최대가능도추정법)
• M-estimation (M-추정법) a.k.a. empirical risk minimization (경험 위험 최 소화법)
• Z-estimation (Z-추정법) a.k.a. estimating equation approach (추정방정식 방 법)

Maximum likelihood estimation (최대가능도 추정법)

최대가능도 추정법은 데이터가 주어질 때.. 데이터를 보고 분포가 무엇인지, 구체적으로는 분포가 가지는 parameter 가 무엇인지 추정할 때 쓰인다. 그래서 '추정법'이라는 말이 붙은 것이고.. '최대가능도'란 가능도 함수를 최대로 하여 이 parameter 를 추정한다는 뜻이다. 그렇다면 가능도 함수에 대한 정의부터 해야겠다.

Definition. Let $\mathbf{x}=\left(x_{1}, \ldots, x_{n}\right)$ be a realization of a random sample $\mathbf{X}=\left(X_{1}, \ldots, X_{n}\right)$ with pdf $f(x \mid \theta)$, where $\theta \in \Omega$. Alikelihood function (가능도함수) is a function of the parameter $\theta$ given the data $\mathbf{x}$ :

• 대분자 X는 random sample 의 뽑히기 전 변수 형태이고, 가능도함수는 이것들이 실제로 뽑혔을 때 값인 small x가 주어졌음을 가정한다.
• 가능도함수는 x보다 추정해야 할 값인 theta에 집중한다. 따라서 notation 에서도 이를 강조한다.
• 세번째 notation 을 보면, 가능도함수도 결국 true theta가 고정되어 있을 떄 realization 값들에 대한 joint pdf 다. 따라서 고정된 theta값에 depend 하는 pdf를 가지고 relization 들을 얻을 확률을 말한다고 할 수 있다.
• 각 xi가 pdf of theta (x)를 iid로 따르는 실현값이라 할 때, 이들의 joint pdf 를 독립이므로 각각의 xi pdf 의 곱으로 표기할 수 있다. (relizations들을 관찰할 확률 = 각각 relization 의 관찰 확률의 곱)

정리하면.. 가능도 함수도 결국은 우리가 계속 봐왔던 데이터에 대한 pdf 에 다르지 않다. 다만, 이를 x중심으로 보는지, theta에 대한 함수로 보는지에 대한 차이다.

Motivation of likelihood function
그렇다면 가능도함수를 왜 최대화할까? 가능도함수를 어디다 써먹을까? 하나의 예시를 두고 이에 대한 likelihood function 을 써보면 이를 알 수 있다.

• Let $X_{1}, \ldots, X_{100} \stackrel{i i d}{\sim} \operatorname{Ber}(\theta)$.
• We observe $x=\left(x_{1}, \ldots, x_{100}\right)$ such that $\sum_{i=1}^{100} x_{i}=93$.
• Suppose we know that $\theta=0.1$ or $\theta=0.9$.
• Which is more likely in this situation?

베르누이 분포를 따르는 확률 sample 들에 x라는 relization 들이 들어왔고, 여기에 0이 7개, 1이 93개인 상황이다. 여기서 likelihood (pmf 값)을 쓰면 다음과 같다. 여기서 likelihood 는 theta 가 true paramter일 때, X1...Xn 을 관찰하는 pmf 값으로 정의한다.

그리고 위에서 세번째 줄에서 가정한 것처럼 세타에 각 값을 넣어보자.

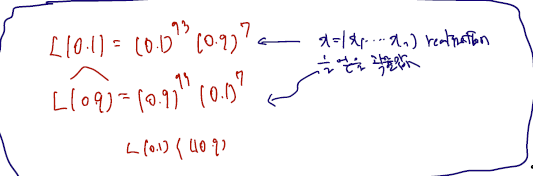
그림에서 나타난 것처럼, 서로 다른 세타를 집어넣고 얻은 계산 값은 $x=\left(x_{1}, \ldots, x_{100}\right)$, 즉 서로 다른 세타일 때 relization 을 얻을 (관찰할) 확률값을 말한다. 그럼 이 함수의 값을 어떻게 해서든 높이는 것이 좋지 않을까? 다시 말해서, 달라지는 likelihood function = pdf or pmf which depedns theta 이므로, 이미 얻은 relization 들을 관찰할 확률이 최대가 되는 세타를 선택하는 것이 좋지 않을까? 가능도함수를 크게 하는 이유가 여기에 있다.

Definition (Maximum likelihood estimator, MLE, 최대가능도추정량). An MLE $\widehat{\theta}$ is a value of $\theta$ maximizing $L(\theta)$ over $\theta \in \Omega$, that is,

• 따라서 이미 정의한 $L(\theta)$를 가장 크게하는 argument, 여기선 세타를 찾고, 이를 진짜 세타에 대한 추정량, 여기서는 함수 $L(\theta)$의 최대화원이라 한다.
• 이때 문제에서 세타가 사는 공간 parameter space 내에서 이걸 찾아야 한다는 게 중요하다.
• 앞의 문제에선.. 관찰된 값 realization 중 1이 93번 등장했는데, 상식적으로 표본평균이 0.93(세타 = 0.93)일 때가 가장 이런 realiazation 을 얻기에 적합할 것이다. 세타를 기준으로 함수를 그리면 다음과 같을 것이다.
  
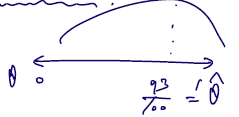
• 여기서 argmax 로 얻은 세타값은 어디까지나 true parameter theta 가 아닌 realization 들을 가지고 얻은 추정량일 것이다. 따라서 hat 을 붙이는 것이다.
• 특별히 $\widehat{\theta}$ 가 $\theta$ 의 최대가능도추정량이면 $\widehat{\theta}^{\mathrm{MLE}}$ 라 쓰기도 한다.

MLE 로 true paramter 을 추정하는 방식은 추정량 자체가 아래의 것들을 만족하는 "좋은" 추정량에 속하기 때문이다. (다른 좋은 이유가 많지만.)

• (Theorem 6.1.3, 일치성) $\widehat{\theta}^{\mathrm{MLE}} \rightarrow \theta_{0}$ as $n \rightarrow \infty$.
• (Theorem 6.2.2, 점근정규성) $\widehat{\theta}^{\mathrm{MLE}} \approx N\left(\theta_{0}, V\right) .(V$ defined in Chap 6)
• (Theorem 6.2.1, 효율성) For any $\mathrm{UE} \widehat{\theta}, \operatorname{Var}(\widehat{\theta}) \geq V$.

MLE 는 따라서 most popular estimators 자주 쓰이는 추정량이다. 다만 한가지 trick 과 같은 것으로.. MLE 를 쓴다는 것은 값 하나를 찾겠다는 말과 같은데, 계산의 편의를 위해 대부분의 경우에 여기에 log 를 씌운 log-likelihood 를 최대화하는 최대화원을 찾는다. $\ell(\theta):=\log L(\theta)$ 이는 가능도 함수가 다루는 pmf 또는 pdf 가 joint 이므로 곱으로 연결되어 있는데, 곱보다 로그를 씌워 합의 문제로 바꾸어 푸는 게 여러모로 편하기 때문이다.

또 한가지 주의해야 할 것은, MLE 는 unique 하게 존재하지 않을 수도 있고, 아예 존재하지 않을 수도 있다. 다시말해 MLE 는 최대값을 찾는 문제이므로 우리가 찾는 세타 값이 2개 이상일 수도, 0개일수도 있다는 것.

How to find MLE
MLE 는 유용하며 잘 알려진 테크닉으로 이를 찾는 일련의 과정이 잘 알려져잇다.

• 위에서 언급한 것처럼 MLE 는 likelihood function 을 최대화하는 최대화원 theta 를 찾으면 되고, 문제를 쉽게 하기 위해 여기에 로그를 씌원 log-likelihood function 을 쓴다.
• 다변수함수의 최대화원을 찾는 anytime solution 은 아쉽게도 존재하지 않는다. 다만 잘 알려진 방법으로는..
• likelihood 함수를 한 번 미분하여 0이 되는 값 중 하나에 세타가 존재함을 가정하고,
• 같은 함수의 이계도 미분이 negative difinite 임을 보이면 함수의 개형 자체가 위로 볼록임을 추론할 수 있으므로 최대값이 존재함을 보이면 된다.

문제1

Example1. 미분 가능의 경우 (MLE of the mean parameter for the normal distribution with known variance). $X_{1}, \ldots, X_{n} \stackrel{i i d}{\sim} N\left(\mu, \sigma_{0}^{2}\right)$, where $\sigma_{0}^{2}>0$ is known. Find the MLE of $\mu$.

• 함수를 어차피 미분할 것이라면 log-likelihood function 에서 mu에 depend 하는 항에 대해서만 식을 새로 쓰면 될 것이란 게 계산을 줄이는 방법이고,
• 앞에 minus 가 붙었으므로 minimization of phi function 문제로 바꾸게 된다.
• 함수를 두 번 미분하면 mu의 모든 공간에서 0보다 큰 값을 알 수 있다. (아래로 볼록) 따라서 minimize at (한 번 미분) = 0 이 되는 점으로 쓸 수 있다.
• 정규분포의 모평균에 대한 MLE 추정량이 표본평균임을 밝혀냈다.

문제2

Example2. 미분 가능의 경우 $X_{1}, \ldots, X_{n} \stackrel{i i d}{\sim} \operatorname{Gamma}(1, \theta)$ with pdf $f(x \mid \theta)=\theta^{-1} \exp (-x / \theta), x>$ 0 . Find the MLE of $\theta$.

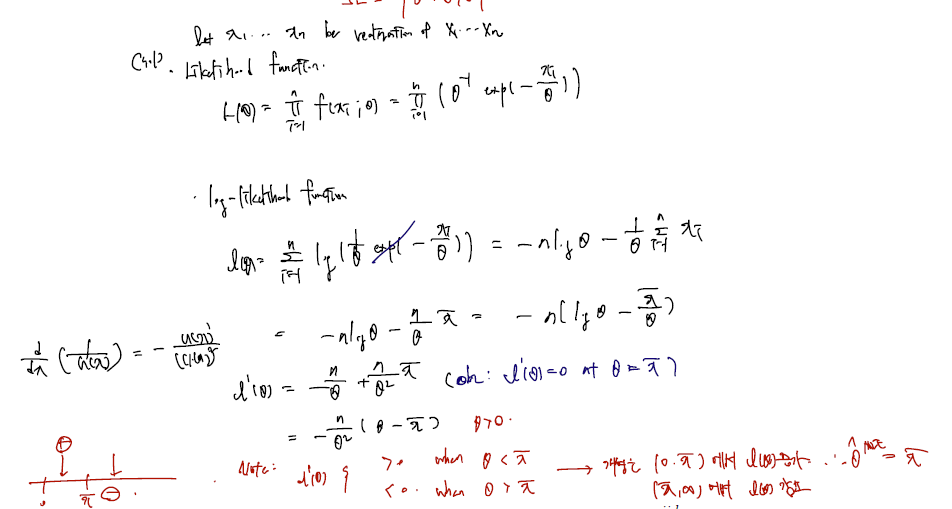
문제3

Example3. 미분 불가능의 경우 $X_{1}, \ldots, X_{n} \stackrel{\text { iid }}{\sim} f(x \mid \theta)=$ $\exp \{-(x-\theta)\}, x \geq \theta$ and $\theta \in \Omega=\mathbb{R}$. Find the MLE of $\theta$.

(Sol) Note that
$L(\theta)=\prod_{i=1}^{n}\left[\exp \left\{-\left(x_{i}-\theta\right)\right\} I\left(x_{i} \geq \theta\right)\right]=\exp \left(-\sum_{i} x_{i}+n \theta\right) I\left(\min _{1 \leq i \leq n} x_{i} \geq \theta\right)$.

이 함수도 역시 thera 에 대한 함수인데.. 문제는 모든 i = 1, ..., n에 대해 다 돌고 난 다음 xi가 가장 작을 때를 기준으로 세타 범위가 있다는 것이다. 구간에 따라 정의된 함수이므로 함부로 미분하는 것은 불가능하고.. 따라서 함수를 그려보는 쪽이 편하다.

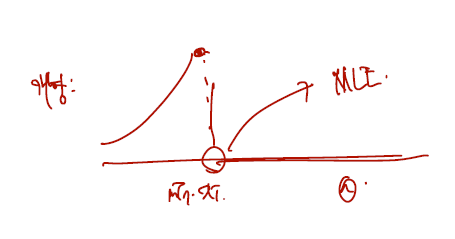
따라서 xi 가 가장 작은 값을 가지는 점이 MLE of theta 가 되는 점일 것이다.
$\therefore \widehat{\theta}=\min _{1 \leq i \leq n} X_{i}$ is the MLE of $\theta$.

문제4

Example4. 하나 이상의 다변수함수 최대화 문제. (MLE of the mean and variance parameters for the normal distribution) $X_{1}, \ldots, X_{n} \stackrel{i i d}{\sim} N\left(\mu, \sigma^{2}\right)$, where both $\mu \in \mathbb{R}$ and $\sigma^{2}>0$ are unknown. Find the MLE of $\boldsymbol{\theta}=\left(\mu, \sigma^{2}\right)^{T}$.

이제는 일변수함수 최대화가 아닌 다변수함수 최대화 문제로 넘어와보자. 만약 정규분포의 두 파라미터인 모평균과 모분산을 둘 다 모른다면 어떻게 해야 하나? 이를 다루는 한 가지 방법은 profiling technique 라 하는데, 찾고자 하는 두 변수 중 한 변수를 고정해두고 나머지 한 변수에 대한 최대화원을 먼저 찾고, 그 다음 고정해둔 변수의 최대화원을 찾는 것이다.

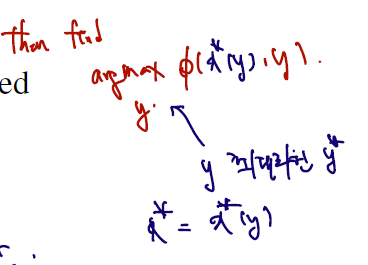
이를 그림으로 표현하면 다음과 같다.

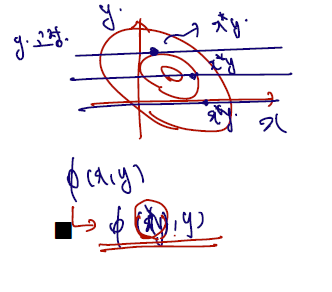
🚩 (1) log-likelihood function 쓰기

🚩 (2) 모분산 고정, 모평균의 추정량 찾기
1.의 log-likelihood function 은 각각 모평균과 모분산을 모두 포함해둔 가능도 함수이나.. 우리가 먼저 찾고자 하는 게 모평균의 추정량이라 했을 때, 모분산은 고정해둔다고 가정하자. 그러면 모분산에 depend 하는 (1)두번째 term 만 살펴보면 되고..

이 식을 minimization 하면 된다. 이 식은, example 1에서도 다루었듯 표본평균으로 계산된다. 따라서 $\ell\left(\mu, \sigma^{2}\right)$ 함수는 maximized at $\widehat{\mu}=\bar{x}$. 그러면 이제 Thus, we fix $\mu=\widehat{\mu}$ 으로 고정하고 $\sigma^{2}$의 값을 찾을 수 있다. 이번엔 maximizing $\ell\left(\widehat{\mu}, \sigma^{2}\right)$.의 문제를 푼다.

🚩 (3) 모분산의 추정량 찾기

계산 결과 분모가 n인 표본분산이 떴다.
Note that

함수는 모분산보다 큰 곳에서 증가하고 작은 곳에서 감소한다. 따라서 이 점이 최대화원임을 알 수 있다. 따라서 다음과 같이 쓸 수 있다.

Therefore, $\left(\widehat{\mu}, \widehat{\sigma}^{2}\right)=\left(\bar{X}, \frac{1}{n} \sum_{i}\left(X_{i}-\bar{X}\right)^{2}\right)$ is the MLE of $\left(\mu, \sigma^{2}\right)$.