[Mathematical Statistics] 4.2 Confidence Intervals

Statistical Inference (통계적 추론) 과 관련해서는, 3가지 정도의 문제가 있다. 1. 추정, (대부분의 경우에서) 분포가 알려졌다고 가정할 때 분포의 모수를 세타로 하여 추정하는 것이다. 2. 신뢰구간, 은 1.에서 추정한 모수를 얼마나 믿을 수 있을 것인지, 추정한 모수에 대한 구간을 정하게 된다. 3. 가설 검정은 이를 바탕으로 O, X를 하는 것이다. 추정에 관한 부분은 앞선 포스트처럼 MLE 를 중심으로 다뤘고, 그렇다면 추정한 모수를 얼마만큼 믿을 것인지에 대해 정리해보자.

4.2 Confidence Intervals

Confidence Intervals 는 우리말로 신뢰구간이며, 다음과 같이 정의한다.

Definition. Let $X_{i} \stackrel{\text { iid }}{\sim} f(x \mid \theta)$ for $i=1, \ldots, n$. Let $\mathbf{X}=\left(X_{1}, \ldots, X_{n}\right)$. For a given $0<\alpha<1$, an open interval $(L, U) \equiv(L(\mathbf{X}), U(\mathbf{X}))$ such that

is a $(1-\alpha) 100 \%$ confidence interval for $\theta$.

The value of $1-\alpha$ is the confidence coefficient or confidence level of the interval.

• 확률변수 Xi는 세타를 모수로 하는 pdf 에서 iid로 추출되었다고 가정한다.
• 알파는 0과 1 사이의 값을 가지며, 알파 = 0.05라면 95% 로 계산되는 이 값을 구간의 신뢰계수 또는 신뢰수준이라 한다.
• Interval은 lower, upper 에서 열린구간으로 정의되며, 따라서 notation 은 추정한 세타가 이 구간 사이에 있을 확률을 뜻한다.

여기서 염두에 둘 것은 세타의 추정도 x라는 realization 으로 하지만 추정된 세타를 얼마만큼(어디까지) 신뢰하는지의 신뢰구간 역시 x의 relization 으로 한다는 것이고.. 조금 더 명확한 해석은 다음과 같다.

해석: 자료를 여러번 관찰하여 $M$ 개의 신뢰구간을 만들었을 때, 대략 $(1-$ $\alpha) 100 \%$ 의 신뢰구간들이 $\theta$ 를 포함한다.

• 주의: $(l, u)$ 가 $\theta$ 를 포함할 확률이 $1-\alpha$ "라고 해석하면 안 된다. $(l, u)$ 는 non-random이므로 하나의 신뢰구간에는 $\theta$ 이 포함/비포함 되어있 을 뿐이다.

신뢰구간은 하나가 아니라 자료를 관찰했을 때 m개라 할 수 있고, 개별 신뢰구간은 고정되어있다. 따라서 개별 신뢰구간을 두고 (l, u)가 세타를 포함할 확률~이라는 표현을 쓸 순 없고 (0 또는 1이므로), 세타가 구간 (L, U) 에 있을 확률이 95% 라거나, 95%의 (l, u) 신뢰구간들이 세타를 포함한다는 괜찮다.

신뢰구간의 또 다른 의미로는, 이전에 true parameter 을 추정하는 추정량들이 (e.g. 모평균을 추정하는 표준평균) 딱 한 점을 찍는 point estimator (점추정량)이었다면, 신뢰구간은 interval estimator (구간추정량) 이다. 점이 아니라 구간을 추정하면, 그만큼의 불확실성을 반영할 수 있는데.. 사실 신뢰수준이 같을 때 이 (불확실성) = (신뢰구간의 길이) 는 작은 것이 좋다.

• The efficiency of a confidence interval is its expected length. (신뢰구간 길이의 expectation 을 efficiency 라고 한다.)
• For two confidence intervals for $\theta,\left(L_{1}, U_{1}\right)$ and $\left(L_{2}, U_{2}\right)$, that have the same confidence level, $\left(L_{1}, U_{1}\right)$ is more efficient than $\left(L_{2}, U_{2}\right)$ if $E_{\theta}\left(U_{1}-L_{1}\right) \leq$ $E_{\theta}\left(U_{2}-L_{2}\right)$ for all $\theta \in \Omega$. (같은 신뢰수준에서 좋은 신뢰구간이란 신뢰구간이 짧은 신뢰구간이다.)

그러나 하나의 분포라면 신뢰구간을 짧게 하면 신뢰수준이 낮아진다. (세타가 그곳에 위치할 확률이 낮아진다.) 이것도 상식에 부합하는 내용.

Case1) 표본의 개체가 정규성을 따를 때

Example (정규성 하에서의 모평균의 신뢰구간 -> 모분산이 unknown일 경우) Let $X_{1}, \ldots, X_{n} \stackrel{\text { iid }}{\sim} N\left(\mu, \sigma^{2}\right)$. For a given $0<\alpha<1$, constrcut a ( $1-\alpha$ ) $100 \%$ confidence interval for $\mu$.

신뢰구간은 주로 모분산이 알려져있을 경우와 알려져있지 않을 경우로 나누어 구하는데, 본문에선 알려져있지 않을 경우만 다루어 이후에 다시 비교할 것이다. 일단 모분산이 unknown 일 경우를 보자. 추정하는 것은 뮤에 대한 신뢰구간이고.. 신뢰수준 (1-알파)% 로 설정한다. 그러면,

(Sol) Let $\bar{X}$ and $S^{2}$ be the sample mean and sample variance. By Theorem 3.6.1, we know that $T=\frac{\bar{X}-\mu}{S / \sqrt{n}} \sim t_{n-1}$.

모분산이 알려지지 않았으므로 모표준편차를 써야 한다. 뮤에 대한 통계량은 위 주어진 T처럼 분모 자리에 모분산 대신 모표준편차 + sample 개수 n의 square root 를 포함하여 쓰는데, 이 통계량은 더이상 정규분포가 아닌 t분포를 따른다. 왜일까?

1)

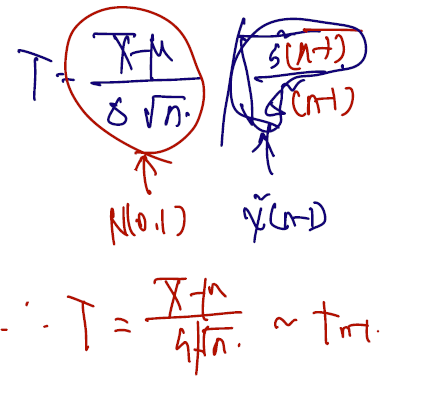
분모 분자에 각각 알려지지 않은 모분산을 알려졌다고 가정하여 끼워넣으면, 위와 같이 식을 변형해서 이해할 수 있기 때문이다. 이 식을 정리하면 다시 아까 확인한 T가 나온다. 그러면 앞쪽의 식은 모분산이 알려진 standard normal 을 따르게 되고, 뒤의 식은 자유도가 n-1짜리인 카이제곱 분포를 따른다. (이에 대한 확인은 스튜던트 정리 - c 번에 있다.) 그리고.. 정의한 T는 그러면 이렇게 정리할 수 있다.

2)

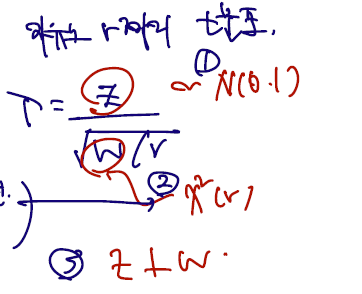
t분포의 정의는 분자가 standard normal 을 따르는 확.변 Z, 분모에 카이제곱(자유도)를 따르는 확.변. W, 이를 다시 자유도로 나눈 것에 square root 을 씌운 확률 변수가 따르는 분포이다. (여기에 3번째로 Z와 W가 indep이라는 것까지면 완성.) 이는, 1)에서 봤던 T 통계량 식의 변형과 완전히 일치하고, 1에서 카이제곱의 자유도는 n-1로 통일되었으므로.. 통계량 T는 자유도 n-1짜리 t분포를 따른다고 할 수 있다.

다시 정리하면, 모분산 없이 표본분산을 사용해 적은 통계량 T는 더이상 정규분포가 아닌 t분포를 따른다. 따라서 신뢰구간도 여기에 해당하는 부분이 수정된다.

Let $t_{\alpha / 2, n-1}$ be the $\alpha / 2$ critical point of $t_{n-1}$ so that $P\left(T>t_{\alpha / 2, n-1}\right)=\alpha / 2$.

$t_{\alpha / 2, n-1}$는 양쪽 꼬리를 다 더했을 때 확률 알파가 되게 하는 분포에서의 점이다. 그림으로는 다음과 같음.

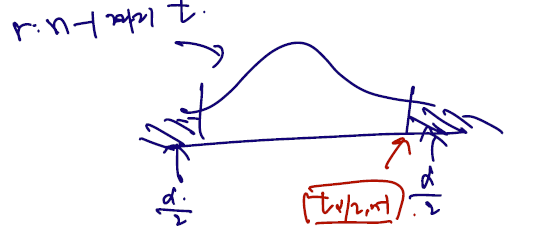
Since the $t$-distribution is symmetric about the $y$-axis, we have

Thus, by the definition, $\mathrm{a}(1-\alpha) 100 \%$ confidence interval for $\mu$ is

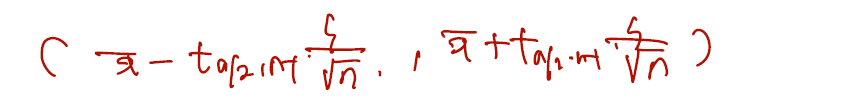
최종적으로 적은 $\mathrm{a}(1-\alpha) 100 \%$ 신뢰수준의 모평균 뮤에 대한 신뢰구간이다. 여기서 모분산이 알려졌을 때와 차이점을 이제 좀 살펴보면..

<모집단은 정규분포를 따를 때, 모평균의 신뢰구간 추정>

1) 모분산이 알려졌을 경우

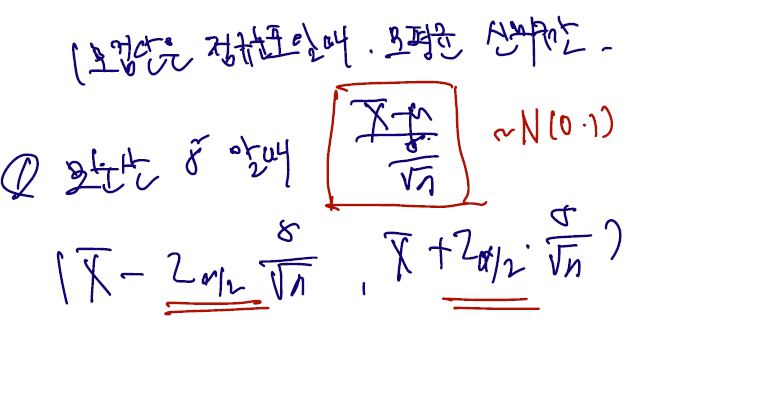
우리가 알던 식 그대로고, 여기서는 정규분포가 여전히 유지된다.

2 모분산이 알려지지 않았을 경우

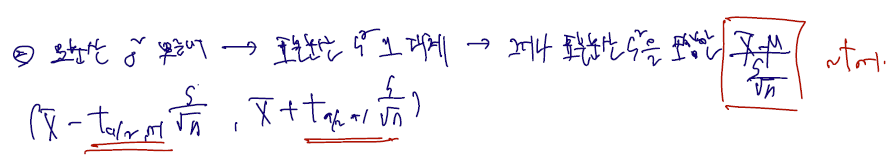
• 다른 건 다 똑같지만,
• 같은 신뢰도 95% 를 유지한다 하더라도 곱해지는 값이 달라지므로 신뢰구간의 길이도 달라진다.
  
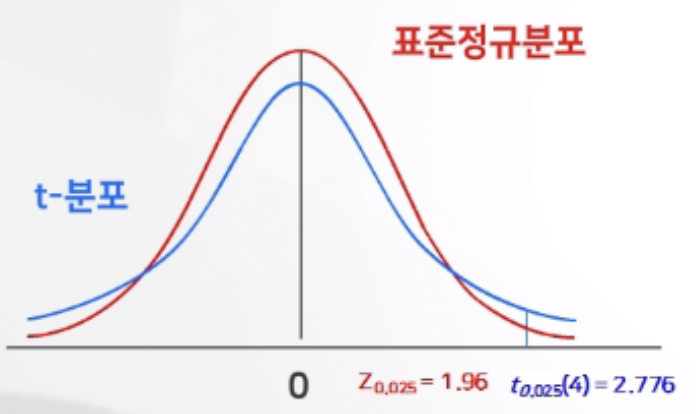
• 예를들어 같은 신뢰도 95% 를 유지하며 추정할 때, 1)의 z위치는 1.96 이고 2)에서는 2.776 이다. 왜 t분포를 가정했을 때 0으로부터 더 먼 곳에 신뢰도 95%로 만드는 점이 위치할까?
• t분포가 정규분포보다 꼬리부분의 확률이 더 큰 분포이기 때문이다. 따라서 이상치도 많은데.. 이럴 경우 점이 더 오른쪽으로 가야 (혹은 더 왼쪽으로 가야) 확률 5% 를 만드는 지점이 나올 것이기 때문이다.
• 다른 말로는 모분산을 알 때보다 모를 때 신뢰구간의 길이가 더 길어질 것이며 (= less efficient), 이는 상식적으로도 이해가 된다. (모르니까 추정을 더 못하지!)

또다른 신뢰구간을 다루는 exact 한 접근을 보자.

Example: 정규성 하에서의 신뢰구간 (분산이 동일한 경우)

• Let $X_{1}, \ldots, X_{n_{1}} \stackrel{i i d}{\sim} N\left(\mu_{1}, \sigma^{2}\right)$ and $Y_{1}, \ldots, Y_{n_{2}} \stackrel{i i d}{\sim} N\left(\mu_{2}, \sigma^{2}\right)$.

이번엔 아까와 다르게 서로 다른 확률 변수를 2개 두며, 각각 normal 을 따르지만 독립으로 다른 분포에서 iid로 추출했다고 가정한다. 여기서 추정하고 싶은 건, 두 확률변수의 모평균의 차에 관심을 가질 것이다. (약의 효과를 검증하는 실험에서 X는 진짜 약을 주고 진짜 약의 효과를 normal 을 따른다고 가정하고 측정하고, Y는 가짜 약을 줬을 때 그에 대한 차이를 비교해볼 수 있다.)

• Let $\Delta=\mu_{1}-\mu_{2}$ be the difference between $\mu_{1}$ and $\mu_{2}$. Suppose we are interested in obtaining a confidence interval for $\Delta$.
• Since $\bar{X} \sim N\left(\mu_{1}, \sigma^{2} / n_{1}\right), \bar{Y} \sim N\left(\mu_{2}, \sigma^{2} / n_{2}\right)$ and $\bar{X} \perp \bar{Y}$, by Theorem 3.4.2,

추정해야 할 것은 두 모평균의 차로 정의된 델타이고, 이걸 뭘로 추정할까.. 하면 역시 각 표본평균의 차가 가장 적절할 것이다. (=: 추정량)

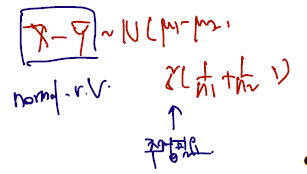
마침 두 표본이 서로 다른 normal 에서 추출되었고, 독립이므로 자유롭게 다룰 수 있는 여지가 많다. 정규분포에서 두 변수가 독립일 때 쓸 수 있는 성질 중 linearity 를 쓰자. 차로 정의된 추정량에서도 normal 을 따르며, 평균은 모분산의 차로, 분산은 각 분산을 더해주면 된다.

그러면 다음과 같이 통계량을 쓸 수 있다.

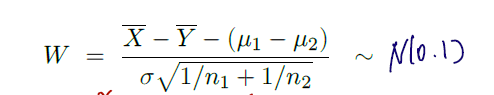
• 두 표준편차의 차를 새로운 확률변수로 보고, 이들의 평균과 분산을 조작하여 standard normal 을 따르는 변수를 만들었다.

우리가 현재 풀고 있는 문제는 분산이 동일한 경우를 가정한다. 만약 분산이 다를 경우 X의 분산과 Y의 분산을 각각 더하는 식으로 편하게 썼겠지만.. 분산이 같다고 한다면? 더 많은 sample 로 더 정확한 분산을 계산할 수 있을 것이다. 이를 반영해서 pooled sample variance 를 쓴다.

• Let $S_{p}^{2}=\frac{\left(n_{1}-1\right) S_{1}^{2}+\left(n_{2}-1\right) S_{2}^{2}}{n_{1}+n_{2}-2}$.

이는 다음에서 도출되었다.

다른 건 없고, 한 번에 같다고 퉁친 분산을 쪼개서 X에서도 내고, Y에서도 내어 편차 제곱의 평균으로 다시 쓴 것이다. 이를 위 식처럼 각 편차 제곱에 weighted가 된 버전으로 볼 수도 있고.. 그냥 단순히 모든 편차 제곱에 평균을 냈다, 로 생각해도 된다.

• Note that $E\left(S_{p}^{2}\right)=\sigma^{2}$.

이렇게 쓴 Sp는 모분산의 비편향 추정량이 되고,

• By Theorem 3.6.1, $\left(n_{1}-1\right) S_{1}^{2} / \sigma^{2} \sim \chi^{2}\left(n_{1}-1\right)$ and $\left(n_{2}-1\right) S_{2}^{2} / \sigma^{2} \sim$ $\chi^{2}\left(n_{2}-1\right)$.

Sp에 분자에 있는 식들을 조금 조작하면 각각이 카이제곱을 따른다는 것을 알 수 있다. 이는 앞서서도 봤던 것이다. (스튜던트 정리 -c)

• Let $n=n_{1}+n_{2}$. Since $S_{1}^{2} \perp S_{2}^{2}$, by Theorem 3.3.1,

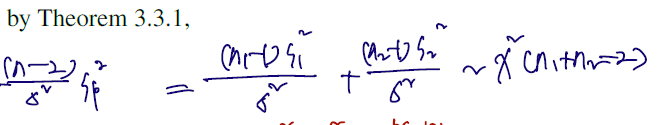
기존에 정의한 Sp와 카이제곱을 따르는 변수를 묶어 다음과 같이 쓴다. Sp를 포함된 식이, 카이제곱(n-2) 를 따른다고 결론지을 수 있다.

• Again by Theorem 3.6.1,
  $W=\frac{\bar{X}-\bar{Y}-\left(\mu_{1}-\mu_{2}\right)}{\sigma \sqrt{1 / n_{1}+1 / n_{2}}} \text { and } V=(n-2) \frac{S_{p}^{2}}{\sigma^{2}} \text { are indep. }$
  thus

이제 마무리이다. 앞서 1. normal (0,1) 을 따르는 통계량 하나(W)를 만들었고, 2. 분산을 그대로 두지 않고 각각의 편차 제곱 평균으로 보아 카이제곱(n-2) 를 따르는 변수 V를 만들었다. 3. 이 W와 V는 표본평균과 표본분산에 depend 하는데, 이 둘은 indep 이다. (by student's theorem) 그럼 이걸 가지고 T를 쓸 수 있고, 이 T는 n-2 자유도의 t-distribution 을 따른다.

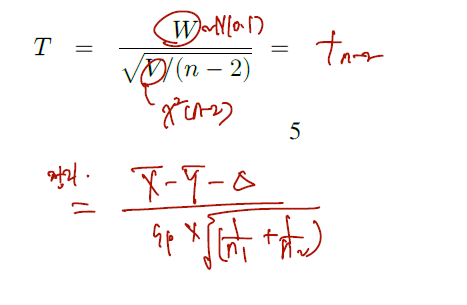
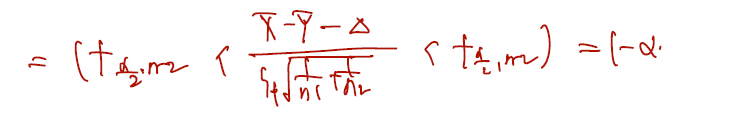
마지막으로 이를 처음 정의한 델타에 대해서 쓰면, 구간의 신뢰도는 다음과 같다.

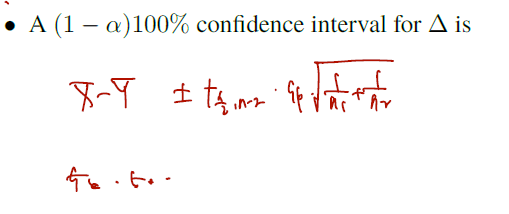
++) 약간의 해석을 덧붙이자면.. 이렇게 t-distribution 을 가지고 만든 신뢰구간의 길이와 정규분포를 또다시 비교할 수 있다.

• 같은 sample 100개일 때, 정규분포의 경우 모분산 X 1/10 이다.
• n1 = 50개, n2 = 50개라하면.. 분산X 1/5 만큼을 신뢰구간 길이로 하므로, 신뢰구간 길이는 더 길어지게 된다.

Case2) 표본의 개체가 정규분포에서 추출되지 않았을 때

이어지는 내용은 앞선 Case1)의 경우와 달리 표본의 각 개체가 정규분포에서 추출되지 않았을 경우이다. 정규성 가정은 생각보다 강한 가정이고 정규성을 따름을 보일 때 사용할 수 있는 성질들이 많기에.. 그렇지 않을 경우도 챙겨둬야 한다. 정규성을 따르지 않을 때는 아래 중심극한정리를 사용하여, 신뢰구간을 근사적으로 만든다.

Theorem (Central limit theorem, 중심극한정리). Let $X_{1}, \ldots, X_{n}$ denote a random sample from a population with mean $\mu \in \mathbb{R}$ and finite variance $\sigma^{2}>0$. Then, the distribution function of

converges to that of the standard normal distribution $N(0,1)$, as $n \rightarrow \infty$.

• 중심극한정리의 기본은, random sample n개와 이들의 모평균, 모분산이 존재(unknown)하지만 어느 분포에서 추출되었는지를 모를 경우이다.
• 이때에도 sample 들을 가지고 만든 표본평균에서 모평균을 빼고, 모분산으로 나눠준 이 새로운 확률변수는 N(0,1)을 따를 것이란 이론.
• n이 무한대로 갈 때 수렴한다.

새로운 확률변수(또는 통계량) Zn의 cdf 도 n이 무한대로 가면 다음과 같이 분포수렴의 형태로 쓸 수 있다. 지금은 내용만 챙겨두고, 나중에 증명하도록 하자.

이를 이용해 exact (정확)이 아닌 근사 신뢰구간을 구하는 예시를 하나씩 볼 것이다. 그 전에 정리를 약간 하자면..

(정규성 하)

• 1. 모분산 아는 경우 + 모평균 신뢰구간 (이 포스트에선 다루지 않음.)
• 2. 모분산 모르는 경우 + 모평균 신뢰구간 ✅
• 3. 다른 모집단 추출 + 모분산이 같은 경우 + 모평균 차 신뢰구간 (등분산 이표본 문제) ✅

(정규성 가정 X) -> 아래에 이어지는 것들.

• 1. 모분산 모름 + 모평균 근사 신뢰구간
• 2. 다른 모집단 추출 + 모평균 차 근사 신뢰구간
• 3. 베르누이분포에서 추출 + 모비율 근사 신뢰구간

순서대로 다룰 것이다.

Example (모평균에 대한 근사 신뢰구간) Let $X_{1}, \ldots, X_{n}$ be a random sample from a population with mean $\mu$ and variance $\sigma^{2}$.

• random sample 이 아무분포에서나 추출되었다고 할 때, 모평균과 모분산이 존재는 하나 주어지지 않았을 경우이다.

• It is well-known that $S^{2} \approx \sigma^{2}$ for all large $n$. Then, by the CLT,
  

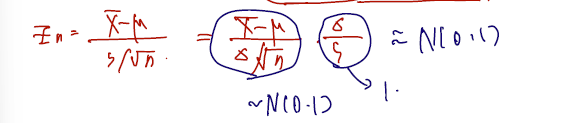
헷갈릴 수 있어 설명을 좀 덧붙이자면.. large n일 때 모분산을 모표준분산으로 근사할 수 있다는 건 CLT 를 쓴 게 아니고 그저 well-known fact 다. CLT 가 들어가는 부분은 이들을 가지고 만든 Zn이, normal(0,1)을 따른다는 것이다. 약간 rigorous 하지 못한 (모분산대신 모표준분산을 끼워넣는 것에서) 부분이 없지 않아 있으나 CLT를 썼다는데 집중하자.

• Therefore,
  $1-\alpha \approx P\left(-z_{\alpha / 2}<\frac{\bar{X}-\mu}{S / \sqrt{n}}<z_{\alpha / 2}\right)=$

The large sample $(1-\alpha) 100 \%$ confidence interval for $\mu$ is

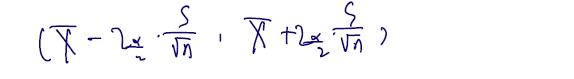
정리하면, CLT 덕분에 분포를 모를 때도 n이 충분한 양으로 주어질 때 계산된 모평균의 신뢰구간을 근사할 수 있게된 것이다. 그런데 이게 정규성 하에서 2. 모분산 모르는 경우 + 모평균 신뢰구간 ✅와 왜 결과 신뢰구간이 다르냐고 할 수 있다. 정규성 하에선 오히려 t(n-1) 을 계수로 사용했기 때문인데.. $N(0,1) \approx t_{n-1}$ for all large $n$.이므로, 모순되는 내용은 아니다.

Example 모평균 차에 대한 근사 신뢰구간
다음으론 정규성 하 -3. 와 대비해서 보면 좋은 내용이다.

• Let $X_{1}, \ldots, X_{n_{1}} \stackrel{i i d}{\sim} \left(\mu_{1}, \sigma_{1}^{2}\right)$ and $Y_{1}, \ldots, Y_{n_{2}} \stackrel{i i d}{\sim} \left(\mu_{2}, \sigma_{2}^{2}\right)$.
• Let $\Delta=\mu_{1}-\mu_{2}$ be the difference between $\mu_{1}$ and $\mu_{2}$. Suppose we are interested in obtaining a confidence interval for $\Delta$.
• Let $\widehat{\Delta}=\bar{X}-\bar{Y}$, where $\bar{X}=n_{1}^{-1} \sum_{i=1}^{n_{1}} X_{i}$ and $\bar{Y}=n_{2}^{-1} \sum_{i=1}^{n_{2}} Y_{i}$.
• Note that
  

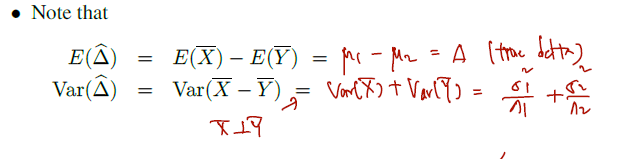
X, Y는 서로 다른 모집단에서 추출되었고 이 둘은 iid 로 어떤 분포에서 추출되었는지 모른다고 하자. 추정하려고 하는 건 이 둘의 모평균의 차이며, 여기서도 표준평균의 차를 쓴다. 운이 좋게도, 분포 과정에 상관없이 다음을 쓸 수 있으므로 차에 대해서도 expectation 과 variance 를 쓸 수 있다.

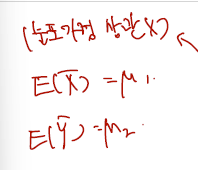
• We know that $S_{1}^{2} \approx \sigma_{1}^{2}$ and $S_{2}^{2} \approx \sigma_{2}^{2}$ for all large $n$.

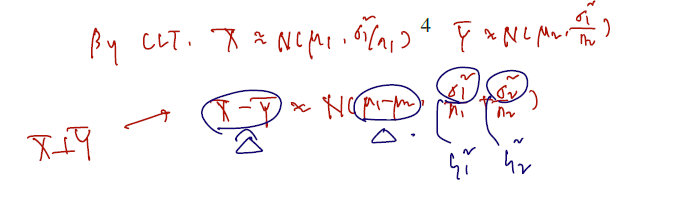
아까와 같이 large n일 때 모분산의 근사를 쓸 수 있고, CLT을 써서 n이 충분하게 주어질 때 이들의 차도 normal 을 따름을 보일 수 있다. 이를 다시 정리하면 다음과 같다.

• Thus, by the CLT,
  $Z_{n}=\frac{\widehat{\Delta}-\Delta}{\sqrt{S_{1}^{2} / n_{1}+S_{2}^{2} / n_{2}}} \dot{\sim} N(0,1) \text { for large } n$

통계량을 정규성 하 -3) 과 비교하면 분자는 같고, 여기선 모분산이 같다는 가정이 없으므로 나눠서 표본분산을 써야한다는 점, 계산한 통계량이 t분포가 아닌 N(0,1)을 따른다는 점이 다르다. (그런데 n이 커질수록 normal 과 t-distribution 은 비슷해질 것이다.) 마지막으로 근사 신뢰구간을 정리하면

• A large sample $(1-\alpha) 100 \%$ confidence interval for $\Delta$ is

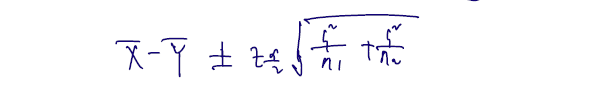
Example (베르누이분포의 성공확률 $p$ 에 대한 근사 신뢰구간)
갑자기 베르누이분포의 성공확률 p는 왜 근사할까? 여기서 보여주고 싶은 건 CLT를 사용할 때 범용성이다. 우리는 random sample 이 정규분포 또는 정규분포가 아닌 분포에서 추출되었다고 가정하고 문제들을 풀었으나.. 지금은 모수를 p로 하는 베르누이 분포에서 추출되었다고 가정해보자. 이렇게 얻은 sample 들을 가지고도 CLT 를 쓰면 normal 을 따르는 통계량을 만들 수 있고, 모수 p의 신뢰구간을 근사할 수 있다는 것이 point 가 되겠다.

• Let $X_{1}, \ldots, X_{n} \stackrel{i i d}{\sim} \operatorname{Ber}(p)$ and $\widehat{p}=\bar{X}$.

베르누이분포는 표본평균이 n개 value 중 1의 개수인 표본비율과 같게 된다. 따라서 표본비율을 근사한다고 하자. 베르누이에서는 $E(X) = p$, $Var(X) = p(1-p)$ 였으므로..

• By the CLT,
  

각각을 뺴고 나누어 통계량을 만들면 이 변수가 N(0,1)을 따른다는 것을 CLT로 알 수 있고,

• One can accurately estimate $p(1-p)$ with $\widehat{p}(1-\widehat{p})$.

분모쪽의 p는 이후 근사신뢰구간에 들어가는 부분인데 알 수 없음이므로 여전히 표본비율 $\widehat{p}$ 으로 근사한다. 이건 CLT를 쓴 건 아니고, 모비율을 n을 무한대로 보내면 표본비율로 근사할 수 있다는 fact 를 쓴 것이다.

• Note that
  

• A large sample $(1-\alpha) 100 \%$ confidence interval for $p$ is
  

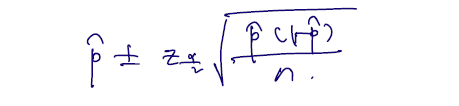
모비율의 신뢰구간을 표본비율만으로 써냈고, 이 경우 통계량이 normal 을 따르게 만든 CLT 의 역할이 중요했다.

이는 근사신뢰구간 예제의 large sample asymptactic 사례에 속한다. 예를들어, X가 포아송 람다를 따르는 분포에서 추출되었을 때에도 true lambda 를 근사하여 신뢰구간을 쓸 수 있다. 휘갈겨 쓴 감이 있긴한데.. 아래와 같다!

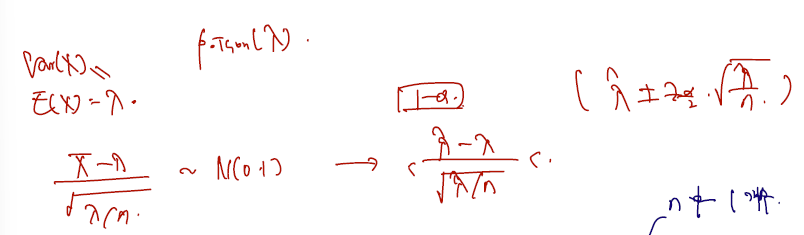
정리 & 소감.

이것이 중심극한정리의 위력이다. n을 무한대로 보내기만 한다면 관찰한 random sample 들만 가지고도 normal (0,1) 따른다고 할 수 있게 하는 것. 다만.. 이에 대한 한 단계 더 근본적인 증명이 필요해보인다. 왜 하필 normal 인지? 계산한 통계량이 (0,1)을 따른다는 확실한 근거는 무엇인지? 가 궁금해지는데, 이 궁금증은 이어지는 챕터에서 확인할 수 있을 듯 하다. (5장에서 중심극한 정리의 증명과 sample 수 n을 무한대로 보낼 때 diverge 와 관련한 증명을 다룬다.)