[Mathematical Statistics] 4.4 Order statistics

4.4 Order statistics

지금까지 random sample X1,..., Xn 은 값의 순서가 없는 변수들이었지만 여기에 순서를 부여한 통계량을 순서통계량이라 한다. 정의를 보자.

Definition. Let $X_{1}, \cdots, X_{n}$ a random sample from a pdf $f(x)$ and $c d f F(x)$ of a continuous-type random variable. Let $Y_{1}$ be the smallest of $X_{i}$ 's, $Y_{2}$ be the 2nd smallest of $X_{i}$ 's, $\cdots$, and $Y_{n}$ be the largest of $X_{i}$ 's. Then, $Y_{1}<Y_{2}<\cdots<Y_{n}$ is called the order statistics (순서통계량) of $X_{1}, \ldots, X_{n}$.

• Another notation: $X_{(1)}, X_{(2)}, \ldots, X_{(n)}$

• X1부터 Xn까지는 continuous-type 변수임을 가정하는데, 이는 discrete 일 경우 tie 를 이뤄 순서를 정할 수 없는 상황을 만들지 않기 위함이다.

• 가장 작은 값부터 큰 값까지를 줄 세워 이를 다시 Y1, ..., Yn으로 이름 붙인다. 이때 순서를 매겨둔 값 자체를 순서통계량이라 한다.

이제 이 순서통계량에 대한 joint pdf 를 쓸 것이다. 결론적으론 다음과 같다.

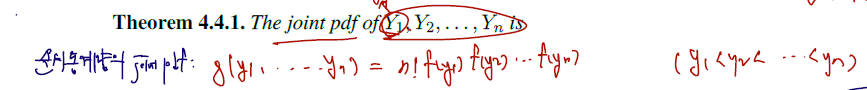
• 각 변수의 pdf 를 곱하고, 앞에 개수 n의 factorial 을 곱해준 형태인데.. factorial 은 y1, ... yn에 매핑되기 위해 xi 가 필요한 경우의 수라 직관적으로 이해할 수 있다. 또는, 아래의 증명을 보자.

n = 3이라고 할 때 y1, y2, y3의 joint pdf 를 쓸 것이다. joint pdf 에 각 증분을 곱한 결과는 아래와 같다.
1)

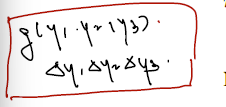
2)

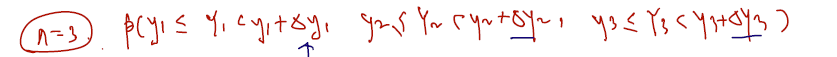
1)을 2)라고 쓸 수 있는 이유는 pdf 의 정의 때문이다. cdf 를 미분한 것이 (또는 적분할 때 들어가있는 form이) pdf 의 정의라 알고있고, 따라서 X가 x와 x + x증분으로 위치할 확률은 pdf 에 x무한소를 곱한 형태로 다시 쓸 수 있다.

이제 2)를 조금 더 전개하면..

3)

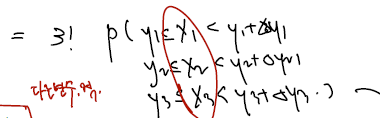
앞에 3!이 붙은 이유는, 사이에 들어간 X1, X2, X3 이 서로 자리를 바꾸어가며 모두 한 번씩 들어가야 하기 때문이다. (그건 y는 순서가 정해진 순서통계량이고 X는 정해지지 않은 확률변수기 때문이다.) 각 확률변수가 독립임을 쓰면, joint pdf를 각 pdf 와 증분의 곱으로 나눠서 다시 쓸 수 있다. 이제 1)과 3)을 비교해 양변을 각 방향에서 증분의 곱으로 나눈다고 하면.. 순서통계량의 joint pdf form 이 다시 나온다.

Notes
joint pdf 를 썼으니 여기서 특정 순위의 변수 하나를 찍고 그 변수의 등장확률이 궁금하다. 따라서 marginal pdf 가 필요하다.

• The marginal pdf of $Y_{k}$ is
  $\begin{aligned} & g_{k}\left(y_{k}\right) \\ = & \int_{a}^{y_{k}} \cdots \int_{a}^{y_{2}} \int_{y_{k}}^{b} \cdots \int_{y_{n-1}}^{b} n!f\left(y_{1}\right) f\left(y_{2}\right) \cdots f\left(y_{n}\right) d y_{n} \cdots d y_{k+1} d y_{1} \cdots d y_{k-1} \\ = & \end{aligned}$

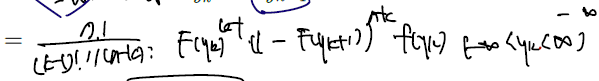
• 왼쪽 끝 a와 오른쪽 끝 b는 각각 -무한대와 +무한대로 바꿔도 무방하다.
• joint pdf 에서 marginal pdf 는 marginal 이 궁금한 변수만 남겨두고 나머지 변수들에 대해 그 변수의 구간을 가지고 싹 다 적분하는 것이었다.
• 안에 들어가 있는 건 여전히 joint pdf form 이고..
• 변수가 각각 -무한대, .., y1, .., yk-1,yk(제외), yk+1, ..., yn, +무한대 순서로 있을 때 예시를 든 것이다.
• 가장 먼저 yn에 대해 yn의 존재가능한 범위를 가지고 적분한다. yn은, 바로 이전 숫자 yn-1부터 무한대 범위까지 존재가능하므로 이 구간에서 적분하낟.
• yk보다 큰 yk+1은 yk보다는 크고 yn보다는 작으나 yn 자체가 yk 일 수 있으므로 무한대까지 적분한다.
• 나머지 변수에 대해서도 마찬가지 원리를 적용한 식이 위 margianl pdf of Yk 식이다.

그렇다면 점을 두 개 찍은 Yi, Yj의 joint pdf 도 궁금할 것이다. 여기서도 같은 원리로, 전체 joint pdf 에서 Yi, Yj 만 제외하고 나머지 변수들에 대해 적분하면 된다. 그런데 이를 위해 Yk의 marginal pdf 를 다른 방식으로 다시 한 번 유도할 것이다.

Remark (Heuristic derivation).

margianl pdf of Yk의 다른 접근이다.

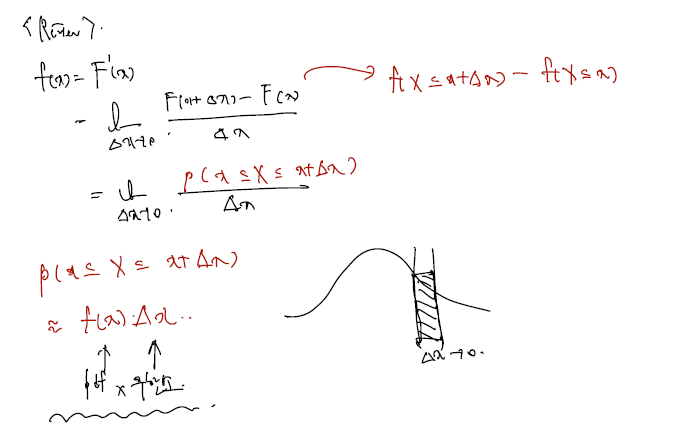
증분이 충분히 작고, yk가 고정된 실수라고 하면 다음과 같이 쓸 수 있다.

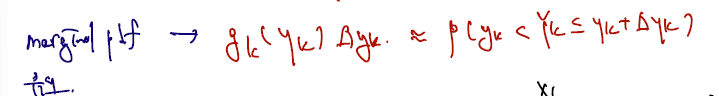
이 marginal pdf를 다시 유도할 것이다. 아래 그림에서 나타내듯, n개 sample 이 주어질 때 Yk 자체는 yk와 yk+ 증분. 사이에 위치한다. 그리고 k-1개는 yk 왼쪽에 위치한다. 나머지 n-k개는 오른쪽에 위치한다.

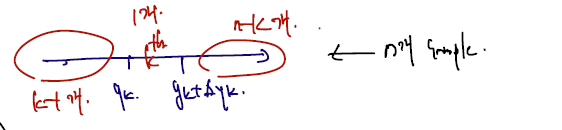
그러면.. pdf 는 일단 3가지 경우에서의 확률과 경우의 수의 곱일 것이다. 경우의 수는? 전체 n!을 각각 (k-1)!, 1!, (n-k)! 로 나눈 것이다. 여기에 확률변수가 들어갈 joint pdf 를 곱하면 다음과 같이 쓸 수 있다.

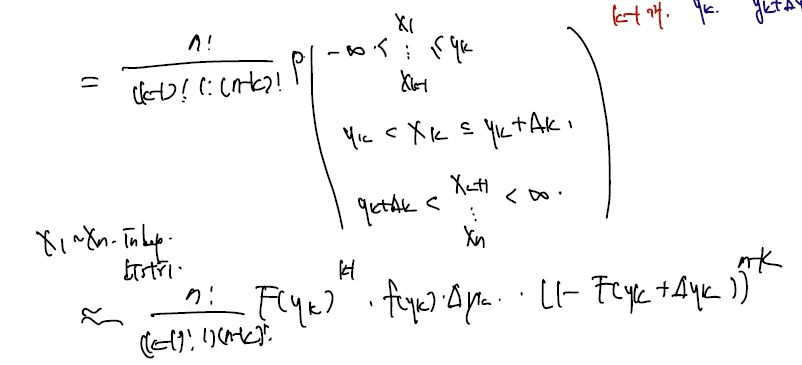
X1~Xn 이 독립이므로 확률들을 cdf 곱으로 나타낼 수 있고.. 예컨대 왼쪽 구간에선 k-1개의 X들이 yk보다 작은 위치에 위치해야 하므로 F(yk)의 k-1승으로 표기할 수 있기 때문이다. F(yk)는 X 하나가 yk보다 작을 확률이고, 이런 X값들이 k-1개 있으므로 이렇게 쓸 수 있다. 같은 방식으로 풀어 쓰면, 좀 더 깔끔하게 marginal pdf 를 정의할 수 있다.

이를 yi, yj 의 경우로 확장하자. i, j가 들어가면 구간 총 3개 (또는 5개)가 생길 것이다. (yi보다 작은 구간, yi, yi와 yj 사이, jy, jy보다 큰 구간)

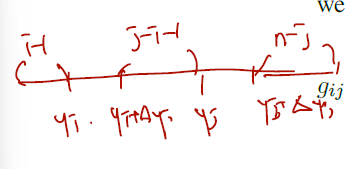
여기서의 joint pdf 는 다음과 같다.

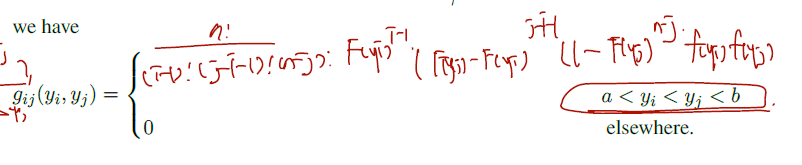
다음으론 이와 연관된 개념인 분위수를 보자.

Qunatiles (분위수)

\subsection*{4.4.1 Quantiles (분위수)}

Definition. Let $X$ be r.v. with continuous cdf $F(x)$. Then, for $0<p<1, \xi_{p}=$ $F^{-1}(p)$ is called p-th quantile (분위수) or $100 p$-th percentile (백분위수) of $X$.

분위수는 cdf 에서 나보다 못한 사람들이 p만큼 될 때, p를 같게하는 cdf 상에서의 값으로 정의된다. 그림으론 다음과 같다. p가 0.95라면 내 아래로 95%의 값들이 있는 것이며, 0.05라면 내 아래로 5%의 값들이 있는 것이다.

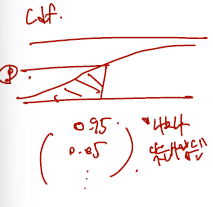
그렇다면.. 내 아래로 0.9만큼이 있도록 하는 true estimator 는 어떻게 근사할 수 있을까? 이를 근사할 때 다른 건 쓰지 않고 주어진 r.v. 만 써서 다음을 보이자.

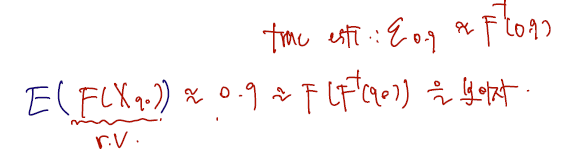
A reasonable estimator for $\xi_{p}$ ? Let $Y_{1}<\cdots<Y_{n}$ be order statistic, and consider
$Y_{k}$, where $k=[p(n+1)]$. Then,

Let $z=F\left(y_{k}\right)$, then $d z=f\left(y_{k}\right) d y_{k}$, so that

여기서 yk는 순서통계량을 따르므로 이에 대한 pdf 를 쓸 수 있고.. 잘 정리하면, cdf 에서 Yk를 집어넣은 기댓값이 원래의 분위수 p를 근사함을 확인할 수 있다. 따라서 이를 표본 분위수 또는 표본 백분위수라 한다.

boxplot
분위수를 가지고는 2가지 plot 을 그릴 수 있다. boxplot 과 q-q plot 인데, boxplot 을 보자.
Example 5.2.4. Data: $56,70,89,94,96, \cdots, 110,113,116(n=15)$
$Y_{1}=56, Q_{1}=y_{4}=94, Q_{2}=y_{8}=102, Q_{3}=y_{12}=108, y_{15}=116$
$h=1.5(108-94)=21 \rightarrow(\mathrm{LF}, \mathrm{UF})=(73,129)$

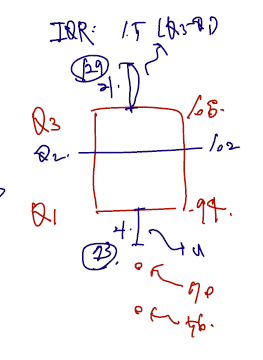
• Q1 은 25 분위수인 지점, Q2는 중앙값, Q3는 75분위수을 쓰고 여기를 박스로 묶는다.
• 위 아래 선은 각각 (1.5 X (Q3-Q1)) 길이만큼 그린다. 이 이상으로 뻗어가는 수치는 이상치로 본다.
• 따라서 여기선 70, 56은 적절히 분석에서 제외할 수 있다.

q-q plot (q-q 그림)

• 관찰한 자료가 특정 분포를 따르는지 직관적으로 확인할 방법이 있을까? 보다 구체적으로 $X_{1}, \ldots, X_{n}$ 이 $X$ 의 임의표본이라 하자. 주어진 분포족에 대하여 (e.g. 정규분포 $N\left(\mu, \sigma^{2}\right)$, 감마분포 $\Gamma(\alpha, \beta)$ 등), $X$ 의 분포가 해당 분포족을 따를는지 확인하고 싶다.

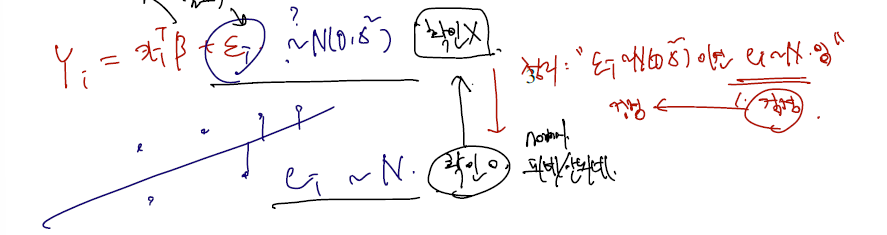
• 주어진 데이터를 가지고 회귀분석을 하는 게 목표인데, 베타의 신뢰구간을 구하고 싶다면 데이터들이 적절히 정규성을 따른다는 검정이 필요하다.

• 따라서 각 데이터 포인트들에서 회귀선까지의 error 들이 normal 을 따른다는 검정이 필요한 것이고..

• 이를 순서통계량으로 확인할 수 있다. error 을 가장 값이 작은 값부터 큰 값으로 줄 세우고, 위에서 계산한대로 이것이 true quantile 의 첫번쨰 분위수부터 마지막 분위수가 되는지 확인한다. 확인을 위해 x는 true quantile, y값은 이에 해당하는 순위의 sample quantile 의 값으로 하여 점을 찍어본다. 물론 true quantile 의 역상은 cdf of normal 에서 찾을 것이다.
  
  

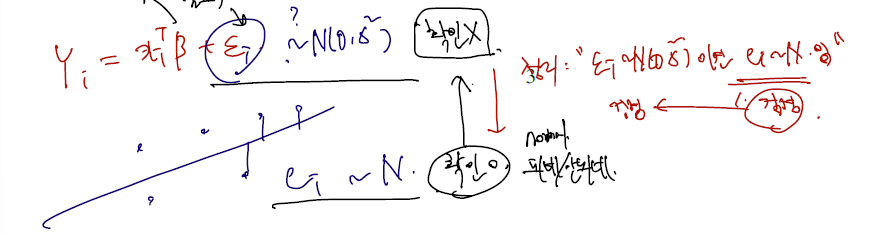
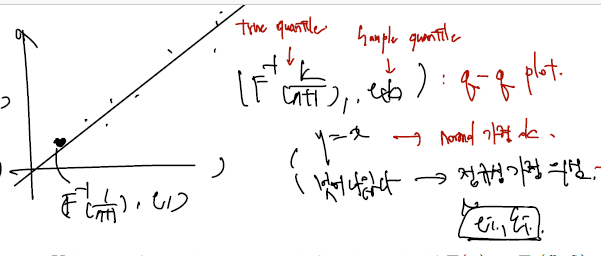
• 만약 sample quantile 과 true quantile 이 일치한다면 (샘플에서의 0.9위치한 점과 실제 cdf 에서 0.9 위치 점) 그래프가 y = x 로 그려질 것이고.. 그렇지 않다면 y = x 선에서 많이 벗어난 형태로 그려질 것이다.

• 만약 y = x 그래프와 가깝다면 normal 가정을 유지할 수 있을 것이고, 그렇지 않다면 정규성 가정을 의심해볼 수 있을 것이다.