[Mathematical Statistics] 4.5 Introduction to hypothesis testing

4.5 Introduction to hypothesis testing (가설검정 개요)

이번 포스팅에서는 기초적인 가설 검정 개요와 이를 활용한 몇가지 예시들을 다룬다. 통계에서 가설검정은 신뢰도와 더불어 또다른 한 축으로 꼽히기 때문에, 아래에 이어지는 내용을 중요한 내용으로 받아들이되 다른 정서를 가지고 이해해도 좋을 것 같다. 일단 용어에 대한 정리가 필요하다.

Definitions
[1] Null and alternative hypotheses.

• Let $X_{1}, \cdots, X_{n}$ be a r.s. from a dist. with pdf $f(x ; \theta), \theta \in \Omega$. Let $P_{\theta}$ be a probability distribution that has pdf $f(x ; \theta)$.

가설과 가설검정에서도 역시 어떤 고정된 unknown 모수를 가지는 pdf 에서, iid sample 들을 가지고 출발한다. 이어지는 내용에서 $P_{\theta}$는 확률분포라 생각하면 된다.

• Statistical hypothesis (통계적 가설):
  $H_{0}: \theta \in \Omega_{0} \quad \text { vs. } \quad H_{1}: \theta \in \Omega_{1}, \quad \Omega_{0} \cup \Omega_{1}=\Omega$
• $H_{0}$ is called null hypothesis (귀무가설; 영가설), and $H_{1}$ is called alternative hypothesis (대립가설).

가설은 통계적 가설과 서술적 가설로 구분된다. 서술적 가설은 말 그대로 언어를 통해 서술된 가설을 이야기하고, 통계적 가설은 기호나 수를 통해 모수에 관한 표현을 한 가설을 말한다. 여기서는 통계적 가설에 집중하도록 하자. 통계적 가설은 다시 귀무가설 $H_{0}$(또는 영가설)과 대립가설 $H_{1}$ (또는 연구가설) 로 나뉘는데, 각각은 주로 다음과 같은 가설로 정의된다.

• $H_{0}$: 귀무가설 / 영가설 -> 기각하고 싶은 가설, 혹은 가설을 오판 시 문제가 더 큰 가설.
• $H_{1}$: 대립가설 / 연구가설 -> 주장하고 싶은 가설.

$H_{0}$, $H_{1}$ 은 사실과 관련해 주장을 담고 있는 하나의 문장, 서술이므로 각각 이 가설이 실제로 진리인지, (실제로 진리인지 여부와 관계없이) 가설을 기각할 것인지 여부에 따라 다음의 2X2 그림을 그려볼 수 있다.

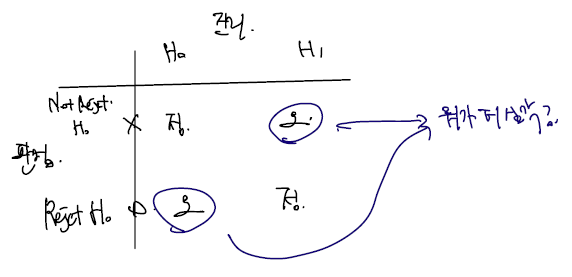
각각은 해당 가설이 실제로 진리인지와 판정을 어떻게 받았는지를 가지고 칸을 구성할 수 있다. 단, $H_{1}$ 판정의 경우 대부분의 가설 검정에서 $H_{1}$을 참이라고 판정하고 싶을 때는 직접적으로 $H_{1}$이 참임을 보이기보단 $H_{0}$ 이 거짓이므로 $H_{1}$가 참이 될 수 밖에 없는 상황을 보이는 귀류법과 같은 검정을 사용하므로 'Reject $H_{0}$' 로 표기한다. 위 표에서, 실제로 $H_{0}$ 가 참일 때 $H_{0}$ 가설을 기각하지 않는 경우와, $H_{1}$ 가 진리일 때 $H_{0}$ 를 기각하는 경우는 올바른, 정확한 판단이라 할 수 있다.

예를들어 내가 범죄자의 범죄 여부를 판정하는 판사라 할 때, 피의자가 실제로 결백하며 판정도 그렇게 하는 경우, 반대로 피의자는 실제로 범죄를 저질렀으며 판정도 유죄라 판단하는 경우가 이에 속한다. 반대로, 피의자는 결백하며 살인을 저지르지 않았는데 살인을 저질렀다고 판정하는 경우와, 피의자가 살인을 저질렀음에도 불구하고 무죄라 판정하는 경우 2가지는 오판이라 할 수 있다. 가설 $H_{0}$와 $H_{1}$를 무엇으로 하는지는 주로 2가지 오판 중 오판이 발생했을 때 윤리적으로 어떤 것이 더 심각한 지를 고려하여 설정할 수 있다. 그 중, 2가지 중 더 심각한 문제를 $H_{0}$ 영가설로 상정한다. 예컨대 위의 예에선, 피의자가 살인을 저질렀는데 살인을 저지르지 않았다고 판정 내리는 경우보다 피의자가 살인을 저지르지 않았음에도 살인을 저질렀다고 판단하는 경우 윤리적 문제가 더 크며 일어나선 안될 것이다. 따라서, $H_{0}$ 을 "피의자는 실제로 살인을 저지르지 않았다" 로 하며, 진리는 그러함에도 $H_{0}$ 을 기각하는 경우, 피의자가 살인을 저질렀다고 판단하는 경우의 확률을 최대한 줄이려 할 것이다.

가설을 두고 진리와 판정의 두 가지 기로에서 저지를 수 있는 두 오류를 1종 오류, 2종 오류라 한다. 1종 오류는, $H_{0}$ 가 실제 참임에도 불구하고 $H_{0}$ 을 기각하는 경우이다. 2종 오류는, $H_{1}$ 가 참인데 $H_{0}$ 을 기각하지 않는 경우이다. ($H_{0}$ 을 받아들이는 경우이다.) 우리는 $H_{0}$ 을 주로 오판 시 문제가 더 큰 것으로 설정한다고 하였고 따라서 1종 오류를 최대한으로 줄이고자 할 것이다. 1종 오류가 일어날 확률을 알파라고 한다면, 확률은 $H_{0}$ 과 $H_{1}$ 각각의 경우에 합이 1일 것이므로 다음과 같이 표기할 수 있다.

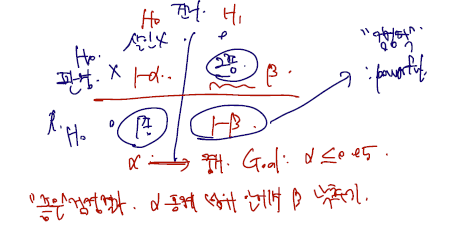
목표("좋은" 검정결과)는 알파를 원하는 수준 이내로 control 하면서 베타를 낮추는 것이다. 이때 각각의 경우, 즉 알파를 원하는 수준 이내로 control 하는 것과 베타를 낮추는 (이 경우엔 1-베타 의 확률을 최대로 한다) 각각의 통계적 방법이 존재한다.

구체적 방법에 대해 알아보자.

• 1종 오류(Type1 error) : An error caused by rejecting $H_{0}$ when $H_{0}$ is true
• 2종 오류(Type2 error) : An error caused by not rejecting $H_{0}$ when $H_{1}$ is true

[2] Two types of errors.

• Test statistic (검정통계량): A statistic (통계량) $T=T\left(X_{1}, \cdots, X_{n}\right)$ for testing $H_{0}$ vs. $H_{1}$

통계량에 대해선 여러번 다뤘을 것이다. Random sample 이 주어졌을 때 T는 규칙 자체이고.. 따라서 계산된 통계량 자체를 자료의 summary 라고 할 수 있다. 결국 보여주고자 하는 것은 random sample 이 기각역(아래에 서술한다)에 속하는지, 아닌지지만 이를 한 번 정리한 통계량을 기준으로 판단한다.

• Rejection region (critical region; 기각역): A set $C$ where $H_{0}$ is rejected, i.e,
  $\text { Reject } H_{0} \text { if } T \in C ;^{1}$

Not reject $H_{0}$ if $T \notin C$.
In other words, the format of every statistical test is"Reject $H_{0}$ if $T \in C$ ".

C는 가설을 검정하기 위한 검정 통계량을 정한 후, T가 이 기각역에 속하는지 아닌지를 판단하기 위한 region 이다. 따라서 검정통계량이 기각역에 속한다면 $H_{0}$를 기각할 것이고, 속하지 않는다면 $H_{0}$를 기각하지 않을 것이다.

그렇다면.. 적절한 기각역의 값은 어떻게 정할 수 있을까? 기각역은 1종 오류의 확률에 한계를 두면서도 2종 오류의 확률을 최소화해야 할 것이다. 예를들어, 내가 탈모를 완화하는 신약의 효과를 입증하고 싶은 연구자라 해보자. 그리고 n = 50 명 중 탈모가 여전히 나타나는 사람의 비율을 통계량으로 하자. 그러면 $H_{0}$ 은 주로 기각하고 싶은 주장을 가설로 하므로 '(신약을 복용한 사람 중 여전히 탈모가 나타나는 사람의 비율) = (한국인의 탈모 비율)', 즉 약의 효과가 없음을 귀무가설로 할 것이다. $H_{1}$은 내가 $H_{0}$ 를 기각함으로써 보이고 싶은 것, '(신약을 복용한 사람 중 여전히 탈모가 나타나는 사람의 비율) < (한국인의 탈모 비율)'을 연구가설로 할 것이다. 이떄 기각역 C는 따라서 (한국인의 탈모 비율) 이 된다.

우리의 목표는 우선 1종 오류 (여기선 '(신약을 복용한 사람 중 여전히 탈모가 나타나는 사람의 비율) = (한국인의 탈모 비율)' 이 실제론 참인데 기각하는 경우) 의 control을 위해 1종 오류의 한계를 정하는 것이다. 이를 size (검정크기) 또는 significance level (유의수준)이라 하며, 다시 말해 1종 오류가 일어날 최대확률을 뜻한다. 다음과 같이 쓸 수 있다.

• A test is of size (검정크기) $\alpha$ or significance level (유의수준) $\alpha^{2}$

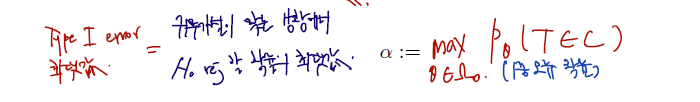
다시말해 알파는 1종 오류가 일어날 최대 확률, 즉 탈모약 검정의 예시에선 귀무가설이 맞는 상황 -> (한국인의 탈모 비율) = 0.3 을 따르는 distribution에서, 귀무가설을 reject 할 확률 -> 통계량이 기각역에 속할 확률을 최대로 한 것이다. '최대'가 들어가는 이유는 귀무가설이 설정한 파라미터 범위에 들어가는 세타가 여러개 일 수 있기 때문이다. 따라서 이 분포 자체도 여러개가 될 수 있으며, 1종 오류가 일어날 확률도 여러개가 될 수 있는데.. 그 중 최댓값을 선택해서 이걸 줄이도록 하는 것이다.

따라서 검정크기 또는 유의수준은 1종 오류의 한계를 정하는 역할이다. 다음은 1종 오류의 한계가 정해졌을 때 이것을 만족하는 기각역 중에서 2종 오류의 확률을 최소화하는 기각역을 선택하는 것이다. 앞의 예시에선, 이어지는 검정력은 2종 오류의 확률을 최소화해서 '(신약을 복용한 사람 중 여전히 탈모가 나타나는 사람의 비율) < (한국인의 탈모 비율)' 이 참일 때 이를 실제로 참으로 받아들일 확률을 최대화할 것이다.

• Power of test (검정력) for $\theta \in \Omega_{1}$ :

• 콤마 뒤에 이어지는 내용이 '실제로 대립가설이 참임' 을 말하고 있고, 콤마 앞의 확률이 '그 경우에 귀무가설을 기각함' 을 말하고 있다. 따라서 이 확률은 Corrct decision 의 확률을 말하고, 이를 검정력이라 한다. 검정력과 2종 오류 확률은 대립가설이 실제로 진리라는 하나의 상황에서 판단에 의해 발생하므로 둘의 확률을 더하면 1이다. 따라서 검정력을 1- (2종오류확률)이라 쓸 수 있다.

추상적인 내용보다 이어지는 서술에서 실제 통계량과 critical region 을 어떻게 construct 하는지를 좀 더 잘 알 수 있다.

Example (A one-sided test for success probability $p$ ). Let $X_{1}, \cdots, X_{n}$ be r.s. from $B(1, p)$. Propose a test of size $\alpha$ for testing

for a fixed $p_{0}$.

베르누이 확률 p에서 뽑인 각각의 랜덤샘플을 가지고 이것들의 표본평균 p가 일반 비율과 같은지(귀무가설) 혹은 작은지 (대립가설) 을 검정하는 방법을 알아보자. 보다 나은 이해를 위해 추가적인 상황을 설정하면.. n = 20명의 사람을 가지고, 디스크를 완화하는 4주짜리 프로그램을 개발하여 이들에게 적용했다고 하자. 디스크의 알려진 일반적인 비율은 $p_{0}$이며 나는 표본으로부터 구한 $p$가 그보다 작음을 보여 개발한 프로그램이 효과적임을 통계적으로 입증하고 싶다. 직장인의 통계이므로 $p_{0} = 0.7$ 이 알려져있고, 프로그램 이후 20명 중 5명이 디스크를 여전히 극복하지 못했고 15명이 디스크가 없었다고 하자. 과연 효과가 있었나? 몇 명을 기준으로 해야 유의수준을 낮출 수 있을까? 의문을 해결해보자.

(sol)

• Test statistic:
  $T\left(X_{1}, \ldots, X_{n}\right)=\sum_{i=1}^{n} X_{i}=: Z, \quad \text { i.e, \# of successes. }$

귀무가설 $H_{0}$을 기각하거나 기각하지 않기 위해서는 통계량이 기각역에 속하는지, 속하지 않는지를 보여야 한다고 했다. 통계량을 construct 하는 방법은 여러가지이나 여기서는 다음의 방법을 따른다고 하자. 여기선 successes 의 수 즉 5명이 S의 값이라 하자.

• Null distribution:
  $S \stackrel{H_{0}}{\sim} B\left(n, p_{0}\right) . \quad\left(X \stackrel{H_{0}}{\sim} P: X \text { follows } P \text { when } H_{0} \text { is true }\right)$

귀무가설을 기각 또는 기각하지 않기 위해 일단 귀무가설이 맞다고 가정하자. 귀무가설 $H_{0}$ 가 참이라고 가정하면, 귀무가설의 주장에 따라 $p=p_{0}$ 일 것이다. 따라서 구한 통계량의 비율이, 모비율을 따른다고 할 수 있으며 기존 B(p)를 n개의 샘플에 대해 $B\left(n, p_{0}\right)$로 확장할 수 있을 것이다. 이처럼 null distribution 은, null 가설 (귀무가설을 h-null 이라 부르기도 한다)이 맞다고 가정할 때 통계량 S가 따른다고 할 수 있는 분포를 말한다.

• Rejection region (critical region):
  $\text { Reject } H_{0} \text { if } S \leq k$
  where the critical value $k$ satisfies $\alpha=P_{H_{0}}(S \leq k)$.

다음으론 통계량 S가 비교할 critical region 에 속하는지를 확인한다고 했다. 여기서 critical region C는 := K 보다 작거나 같은지 (또는 문제에 따라 크거나 같은지) 로 정의된다. 그렇다면 여기서 K는 어떻게 정하는가? 미리 상정해둔 유의수준 알파의 값을 넘지 않도록 하는 선에서 정한다. 예컨대 k 가 높아지면 높아질수록 귀무가설을 많이 reject 할 것이므로 알파 값은 높아질 것이며 1종 오류도 덩달아 증가할 것이다. 따라서 먼저 이를 최소화하는 것을 목표로 하자.

	True State of Nature
Decision	$H_{0}$ is True	$H_{1}$ is True
Not reject $H_{0}$	Correct Decision	Type II Error
Reject $H_{0}$	Type I Error	Correct Decision

where the critical value $k$ satisfies $\alpha=P_{H_{0}}(S \leq k)$.

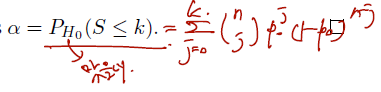
• 알파 즉 1종 오류의 확률을 최대화하는 값은 다음과 같이 다시 쓸 수 있다.
• 귀무가설이 맞을 때 기각역에 속할 확률(= 귀무가설을 기각할 확률)의 최댓값이며, 귀무가설이 맞을 때는 binomial 분포이므로 이 확률을 다 더할 수 있을 것이다. 예컨대 k = 11이라면, 확률 p를 따르면서 n=20명 중 디스크가 1명일 경우부터 11명일 경우까지를 다 더한다. k = 12 라면, 디스크가 1명일 경우부터 12명일 경우의 확률까지를 다 더한다. S<=11 일 때 기각하는 것이 1종 오류의 확률이 더 높을까 S<=12 일 때 기각하는 것이 1종 오류의 확률이 더 높을까? 알파값에 따라, S<=12 일 것이다. 이를 다음과 같이 쓸 수 있다.

Note: Assume $n=20, p_{0}=0.7$, and $\alpha=0.15$. Then, $P_{H_{0}}(S \leq 11)=.1133$ and $P_{H_{0}}(S \leq 12)=.2277$.
Hence, a test of size .15 rejects $H_{0}$ if $S \leq 11$.

• 유의수준 0.15로 유지하고 싶을 때 (이는 연구 전에 미리 제출한다.) K=11일 때의 test 1는 유의수준 밑으로 1종 오류 확률이 내려왔으므로 가능할 것이고, test 2는 유의수준을 넘어 불가능할 것이다.
• 따라서 S<=11 20명 중 디스크가 11명 이하라면 유의수준 0.1133에서 귀무가설이 기각되고, 대립가설을 채택할 수 있다.
• S<=12, 20명 중 디스크가 12명 이하라면 유의수준 0.2277에서 귀무가설을 기각하고, 대립가설을 채택할 수 있으나 유의수준이 미리 상정해둔 0.15를 넘어선다.

Compare power function for $S \leq 11$ and $S \leq 12$.

다만 1종 오류의 확률을 control 했으면 2종 오류도 최소화하려는 노력이 필요하고, 이는 power function 을 최대화하면 된다. 아래는 k=11, 12 각각의 경우에서 power function 그림이다.

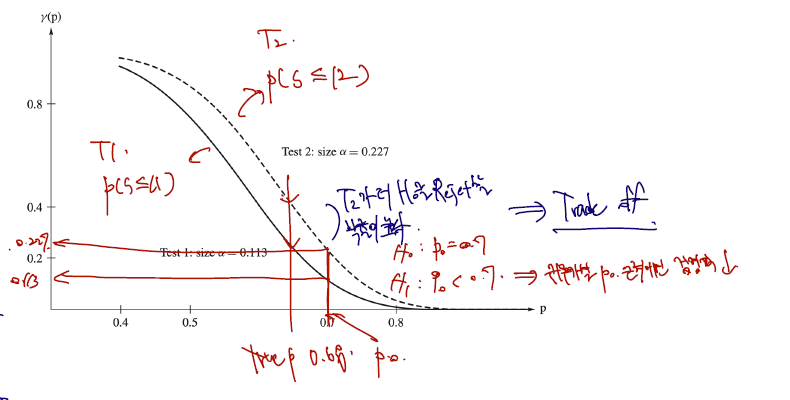
• 위 그래프가 S<=12 를 기각역으로 할 경우이고, 아래의 그래프가 S<=11 을 기각역으로 할 경우이다. power function 은 말그대로 주장하고 싶은 대립가설이 실제로 참일 때 참으로 판단하는 확률이므로, 높을수록 좋다.
• 따라서 이번엔 S<=12 를 기각역으로 할 경우가 power function 의 값이 높고, 2종 오류는 최소화될 것이다. 왜 trade-off 가 나타날까?

	True State of Nature
Decision	$H_{0}$ is True	$H_{1}$ is True
Not reject $H_{0}$	Correct Decision	Type II Error
Reject $H_{0}$	Type I Error	Correct Decision

• 표를 다시 봐보면.. S<=12 를 기각역으로 한다는 건 진리가 무엇이든 $H_{0}$ 기각을 더 많이 한다는 뜻이다. 따라서 이 행에 해당하는 확률이 전체적으로 증가하는데, 이때 1종 오류의 확률도 증가한다. S<=12 에서 1종 오류 확률이 높았던 이유이고,
• 동시에 not reject $H_{0}$의 확률들은 다 감소한다. 자연히 $H_{1}$가 참일 때 $H_{0}$을 기각할 확률도 감소하고, 따라서 2종 오류의 확률도 감소한다.
• 기각역 주위의 확률에선 검정력이 낮을 것이다. 이는 직관적으로도 이해가 된다. 현재 p0 = 0.7 인데 실제 계산도 0.7 라면 같은 분포를 따름을 뜻하므로 같은 분포확률을 가질 것이다. 프로그램 후 0.7의 디스크 환자 비율이 나타났다면, 귀무가설을 기각할 확률은 각각 0.113, 0.226 밖에 되지 않을 것이다. 여기서도 여전히 기각을 더 많이하는 test 2가 검정력이 조금 더 높지만.