[Mathematical Statistics] 4.6 Additional comments about statistical tests | 4.7 Chi-square tests

4.6 Additional comments about statistical tests

Test statistics 를 만들고, 이들이 따르는 분포를 근사한 다음 rejection region 을 만드는 일련의 검정과정을 다양한 조건에서 해보자. 아래 이어지는 내용들은 다음과 같다.

• 일표본 z검정, 양측가설
• 일표본 t검정, 양측가설
• 이표본 등분산 t검정, 양측가설
• 카이제곱 검정 (적합성 검정 / 동질성 검정 / 독립성 검정)

Example1

Example 1 (Large-sample two-sided test for testing population mean $\mu$, "일표본 $z$ 검정, 양측가설").
Let $X_{1}, \cdots, X_{n}$ : r.s. from a dist with mean $\mu$, variance $\sigma^{2}$. Propose a large-sample test of approximate size $\alpha$ for testing

for a fixed $\mu_{0}$.

이전에 검정했던 가설이 H{1} 대립가설서 모평균이 가설 내에서 상정한 평균보다 크다, 또는 작다라는 단측가설이었다면 이번엔 양측가설이다. 양측가설은 H{1} 대립가설로 같다를 제외한 범위를 모두 포함할 수 있도록 다르다 ('작다', 또는 '크다) 로 세우는 것이며, 따라서 귀무가설은 이와 반대로 모평균과 가설 내 평균이 같다, 라고 세우게 된다. 아래 이어지는 내용을 보면 조금 더 확실해진다.

(sol) Intuitively, we may want to reject $H_{0}$ iff $\bar{X} \leq h$ or $\bar{X} \geq k$ s.t. $\alpha=P_{H_{0}}(\bar{X} \leq h$ or $\bar{X} \geq k)=P_{H_{0}}(\bar{X} \leq h)+P_{H_{0}}(\bar{X} \geq k)$. Since the asymptotic distribution of $\bar{X}$ is symmetric, we may prefer to find $h$ and $k$ such that $P_{H_{0}}(\bar{X} \leq h)=P_{H_{0}}(\bar{X} \geq$ $k)=\alpha / 2$.

전체 유의수준 알파에서의 검정이라면 추출한 표본이 symmetric 할 것이기 때문에 각 범위에서 각각 알파/2 가 되는지를 확인하면 된다. 이 검정을 위해 역시나 test statistics -> null distribution -> rejection region construct 의 가정을 하나씩 거치자.

• Test statistic:
  

• Null distribution:
  

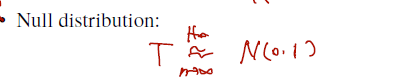
• Rejection region:
  

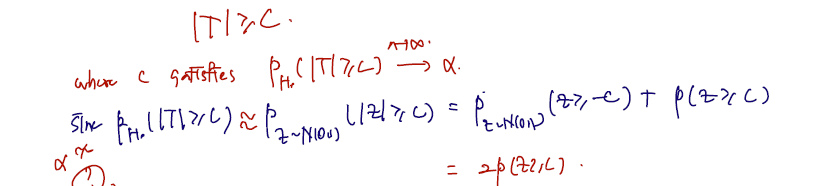
T가 C보다 작다 또는 크냐를 한 번에 묶기 위해 절댓값으로 표기하고, 이것보다 클 때 Reject 한다는 내용을 담으면 된다. 그렇다면 이 영역에서 통계량이 속할 확률을 유의수준 알파라 할 수 있으며, 정규화 이후 N(0,1)에서 C보다 클 확률에 2배를 취한 것이다. 따라서 C가 취하는 분위수도 다음과 같을 것이다.

Approximate power function 은 다음과 같다.

• Approximate power function 은 대립가설이 맞다고 했을 때 귀무가설을 reject할 확률이다.
• 따라서 그래프로 이해하면 x축은 모평균이고, 이 모평균이 변함에 따라 귀무가설을 reject 할 확률도 따라 변하는데 이 확률을 표시해둔 것이다.

이를 그림으로 나타내면 다음과 같다.
Figure: (Approximated) power curve for Example 4.6.1 when $n=20, \mu_{0}=$ 30000 and $\sigma=5000$ with different values of $\alpha$.

• 알파 = 0.05 는 기각확률을 가져다쓴 유의수준으로 이 그래프를 따라가보면 $\mu=\mu_{0}$ 일 때(귀무가설이 참일 때) 귀무가설을 기각할 확률이 0.05 를 찍는 것을 알 수 있다.
• 알파 = 0.01 일 때도 마찬가지로 확률 0.01 을 확인할 수 있고
• 추가로 귀무가설이 주장하는 범위 근처에서는 검정력이 매우 낮을 수 밖에 없음을 직관적으로 해석할 수 있다. (검정력이란 건 대립가설이 참일 떄 대립가설이 참이라고 말하는 것인데, $\mu$ 자체가 어디있느냐에 따라 확률이 계속 달라지고, $\mu=\mu_{0}$ 귀무가설이 주장하는 근처에 있으면 헷갈릴 수 밖에..)
• 이 그래프는 검정력과 1종 오류 사이 trade-off을 나타낸다. 예컨대 알파 0.01 은 1종 오류의 확률은 0.01 로 낮으나 그만큼 진리와 상관없이 귀무가설을 reject 하지 않을 것임을 나타낸다. 자연히 2종오류의 확률, 대립가설이 참일 때 귀무가설을 reject 하지 않을 확률도 높아지므로 trade off 를 확인해볼 수 있다.

Example2

Example 2 (Exact two-sided test for testing population mean $\mu$, "일표본 $t$ 검정, 양측가설").
We go with the same setting of Example 6.4.1 but additionally assume $X$ follows the normal distribution. Propose a test using of size exactly $\alpha$.

다음은 X 자체가 normal distribution 을 따르는 확률변수에서 표본을 추출했을 경우이다. 아래를 보면 과정은 다 같지만 test statistics 이 n-1짜리 자유도의 t분포를 따르고 있고, 따라서 1-알파/2 quantile 역시 t분포에서 추출해야 함을 보이고 있다.

이와 같이 t분포를 사용해서 검정하는 것을 (귀무가설 하 통계량이 t분포를 따름을 보이고 기각역도 여기서 construct 하는 것을) t검정이라 하고, 위의 example 1예시처럼 z분포라면 이를 z검정이라 한다.

여기서 한 가지 내용을 좀 더 추가할 수 있다. 만약 내가 새로 만든 수학 문제집의 효과를 입증하고 싶다면, t검정을 사용해야 할까 z검정을 사용해야 할까? 검정에 있어 어떤 분포가 더 보수적일까?

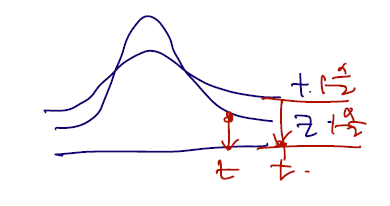
t분포는 z분포보다 꼬리가 길다고 하였다. 따라서 같은 유의수준 알파를 적용하더라도, 위치해있는 분위수가 다르고 그에 따라 통계량이 범위에 속할 가능성도 달라질 것이다. t분포가 z분포보다 꼬리가 길고, 따라서 1-알파/2 분위수의 위치도 더 오른쪽에 있다. (양수라 가정했을 때). 따라서 같은 통계량이라면 t분포보다 z분포가 기각을 할 확률이 높고, 만약 귀무가설을 문제집을 통해 평균이 달라졌음을 보이고 싶다면 (기각을 해야 좋으므로) z분포를 사용하는 것이 이득일 것이다.

같은 논리로 내가 소비자라면 조금 더 보수적인 판단을 위해 t분포를 (효과 없음을 대부분 주장하고 싶음), 규제기관일 경우 t분포를 주로 사용하되 z분포도 사용해볼 수 있다. 그러나 어느 경우에서건 t분포가 기각한 통계량일 경우 z분포에서도 기각될 것임을 예측해볼 수 있다.

Example 3

Example 4 (Exact two-sided test for testing the homogeneity of two-sample population means with equal variance, "이표본 등분산 $t$ 검정, 양측가설"). Let $X_{1}, \cdots, X_{n_{1}}$ be r.s. from $N\left(\mu_{1}, \sigma^{2}\right)$ and $Y_{1}, \cdots, Y_{n_{2}}$ be r.s. from $N\left(\mu_{2}, \sigma^{2}\right)$. Propose a test of size $\alpha$ for testing

이번엔 모평균의 값 자체에는 관심이 없고, 단지 서로 다른 두 집단 (분산이 같고, 모평균만 다른) 이 있을 때 이들의 samples 들을 통해 모평균이 같은지, 또는 다른지를 검증해내려 한다. 역시나 같은 과정을 거치면

이전에 등분산 이표본에서 모평균 차의 신뢰구간을 구한 때와 비슷한 통계량을 쓴다. pooled variance 를 그대로 갖다 쓰는데, 이는 각 집단의 편차 제곱합을 전체 수로 나눠서 두 이 표본에 대해 둘을 포괄할 수 있는 분산을 계산해내는 방법이었다.) 이 통계량은 자유도 n-2 짜리 t분포를 따랐었고.. 따라서 양측 검정 시 n-2 자유도의 t distribution 에서 rejection region 도 만들어진다.

4.7 Chi-square tests (카이제곱검정)

이제까지 다룬 검정 방법이 연속형 변수에 대해 적용할 수 있는 가설 검정 방법이라면, 카이제곱검정(chi-square test)은 범주형 자료에 적용할 수 있는 통계적 가설검정 방법 중 하나이다. 카이제곱검정은 다음과 같이 세 종류로 구분된다.

• goodnessof-fit test (적합성검정; GOF test)
• homogeneity test (동질성검정)
• independence test (독립성검정)

일단 각 검정에 들어가기 전에 공통적으로 사용되는 fact 를 보자. 아래의 fact 는 n = 자료 수만큼의 서로 다른 확률변수들이 있을 때 각각의 확률변수들의 통계량의 합이 카이제곱을 따름을 보인다.

[1] Motivation.

통계량 Q는 각 확률변수에서 (관찰된 값- 기대도수)의 제곱을, 기대도수로 나눈 값을 더하게 된다. 그리고 이를 n개 자료에서 k개 범주의 자료가 있을 때 다음과 같이 확장할 수 있다.

In general, let $\boldsymbol{X}=\left(X_{1}, \cdots, X_{k}\right)^{T} \sim \operatorname{Multi}\left(n,\left(p_{1}, \cdots, p_{k}\right)\right)$ where $X_{1}+\cdots+$ $X_{k}=n$ and $p_{1}+\cdots+p_{k}=1$. Then, it is known that

식은 복잡해보일 수도 있지만.. 자료에 적용해보면 쉽다. n = 11 명이 있을 때, 자취하는 학생들과, 기숙사 사는 학생들, 통학을 하는 학생들의 수가 각각 3, 4, 4 라고 한다면 통계량은 다음과 같다.

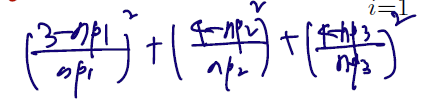
역시나 관찰도수에서 기대도수를 뺀 것을 제곱한 것이 분자로, 기대도수가 분모로 갔다! 이 자료에선 n = 11, p1 = 3/11, p2 = 4/11, p3 = 4/11 이 될 것이다. 그리고 이 Q 통계량은 자유도 3-1=2짜리 카이제곱 분포를 따를 것이다. 위에서 본 이항분포의 경우 k=2이므로 카이제곱 1을 따랐던 것이다.

범주형 변수에서 만들어낼 수 있는 이런 통계량으로, 3가지 서로 다른 검정을 할 수 있다. 적합성 검정이란 분포의 모수 $p_i$가 알려진 비율 $p_{i0}$ 와 같은지 (모든 범주에 대해) 검정하는 것이다. 따라서 $p_i$는 unkown 이고, $p_{i0}$는 아는 값이다. 아래를 보자.

[2] Goodness-of-fit test (적합성검정).

• Let $\boldsymbol{X}=\left(X_{1}, \cdots, X_{k}\right)^{T} \sim \operatorname{Multi}\left(n,\left(p_{1}, \cdots, p_{k}\right)\right)$ where $X_{1}+\cdots+X_{k}=$ $n$ and $p_{1}+\cdots+p_{k}=1$
• Null hypothesis:
  $H_{0}: p_{1}=p_{10}, p_{2}=p_{20}, \ldots, p_{k}=p_{k 0}$
  where $p_{10}, \ldots, p_{k 0}$ are known positive constants with $p_{10}+\cdots+p_{k 0}=1$.

자료는 n명에 대해 k개 범주를 가지고 추출되었다고 해보자. 각 수를 모두 합하면 n이 나오고, 각 확률은 0 보다 크다. 귀무가설은 분포의 모수가 알려진 parameter 와 모두 일치하다고 보는 것이다. 위의 예시로부터

자취생의 비율이 알려진 (국가 내 비율이 25%라 했을 때) 비율 25%와 같은지, 기숙사, 통학에서도 각각 같은지.. 검정하는 것이다. 이에 대한 통계량은 아래와 같다.

• Test statistic:
  $Q=\sum_{i=1}^{k} \frac{\left(X_{i0}-n p_{i}\right)^{2}}{n p_{i0}}$
  통계량은 실제 계산되어야 하는 값이므로 알려진 숫자만 쓴다. 그리고 이렇게 계산된 Q 값은 실제 값이 도수가 X에 들어가므로 아래와 같다.

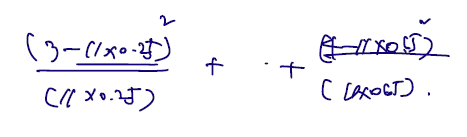
이 값은 실제 도수에 기대도수를 뺀 것을 제곱한 것으로 여기서 차이가 기각역보다 많이 나는지를 검증하게 된다. 우선, 위의 fact 에 따라 이 통계량이 귀무가설 하 k-1 자유도의 카이제곱을 따름을 보일 수 있고,

• Null distribution:

  $Q \stackrel{\mathrm{H}_{0}}{\approx} \chi^{2}(k-1)$

• Rejection region
  

$Q >= C$로 기각역을 설정한 것은 제곱의 형태이므로 기각역보다 크면 두 모수가 다르다고 하여 기각하도록 하였다. 여기서는, 단측 검정이므로 주어진 designed size 알파 유의수준에서 검정하여 카이제곱 1-알파 quantile 이 C가 되도록 한다.

[3] Homogenity test (동질성 검정)

위의 적합성 검정은 알려진 known parameter 가 숫자로 존재하여 사실은 같다, 다르다의 검정보다 자료의 통계량이 known paramter 인지 아닌지를 검정하는 것에 가까웠다. 그러나 다음에 이어질 두 검정은 모수의 값이 아닌 자료 내에서 관계만 검정하게 된다. 특히나 k categories 를 가지는 서로 다른 독립의 분포를 따르는 변수들이 등장한다.

• Consider two independent multinomial distribution with $k$ categories:
  $\begin{aligned} & \mathbf{X}_{1}=\left(X_{11}, \cdots, X_{k 1}\right)^{T} \sim \operatorname{Multi}\left(n_{1},\left(p_{11}, \cdots, p_{k 1}\right)\right) \\ & \mathbf{X}_{2}=\left(X_{12}, \cdots, X_{k 2}\right)^{T} \sim \operatorname{Multi}\left(n_{2},\left(p_{12}, \cdots, p_{k 2}\right)\right) \end{aligned}$

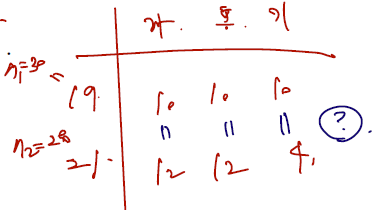
그러나 이번에도 자료 하나를 생각해보면 어렵지 않게 확장이 가능하다. X1을, 19 학번 중 자취, 통학, 기숙사를 하는 사람들을 조사한 확.변이라 보고, X2를 21학번 확.변이라 보면 된다. 그리고 확률 p들은 각각 모분포의 모비율이라 보자. 이런 상황을 가정할 경우 변하는 것은 자유도 계산 부분 뿐이다.

• Null hypothesis:

  $H_{0}: p_{11}=p_{12}, \cdots, p_{k 1}=p_{k 2}$

  귀무가설은 집단 내 비율이 동등하다는 것이다. "19학번과 21학번 자취의 비율이 동등하다", 통학도, 기숙사도 비율이 동등하다.. 라는 것.

• Test statistic:

  $Q=\sum_{j=1}^{2} \sum_{i=1}^{k} \frac{\left(X_{i j}-n_{j} \widehat{p}_{i j}\right)^{2}}{n_{j} \widehat{p}_{i j}}, \quad \widehat{p}_{i j}=\frac{X_{i 1}+X_{i 2}}{n_{1}+n_{2}}, j=1,2$

  통계량은 똑같이 관찰 도수에서 기대도수 추정량을 뺀 것에 기대도수 추정량으로 나눈 것이다. 이때 모비율을 모르므로 p hat 을 구하게 되는데, 귀무가설이 맞다고 가정했을 때의 통계량이므로 자취생의 비율을 구하고 싶다면 위의 표에서 (10+12)/(30+28)이 된다. 이는 p11과 p12 에서 같다.

• Asymptotic null distribution:

  $Q \stackrel{H_{0}}{\approx} \chi^{2}(\mathrm{df}),$

  where $\mathrm{df}=(2 k-2)-(k-1)=k-1$.

df 는 degrees of freedom 자유도의 약자다. 그리고 위의 표에서 구할 수 있는 것까지 구했을 때 나머지 알 수 있는 모수를 뺴면 된다. 2k-2는 귀무가설이 없을 때 총 모수 개수이다. (k-1) 을 각각 19학번, 21학번에서 알 수 있을 것이다. 귀무가설이 맞을 때는 19, 21 학번에서 모수가 같으므로 k-1만 알면 될 것이다. 이처럼 df 는 귀무가설이 없을 때 모수 개수에서 맞을 때 모수개수를 빼서 구한다.

[4] Independence test (독립성검정).
마지막으로 독립성 검정은 X, Y 두 변수가 각각 m개와 k개의 카테고리가 있다고 했을 때 (19,20,21,22,23 학번과 자취,통학,기숙사라 하자.) 이 들의 모비율이 각 marginal 비율의 곱, 즉 독립이라는 검정을 하고 싶을 때 사용한다. 만약 독립임을 보였을 경우 두 X, Y 변수에 유의미한 관계가 없다고 말할 수 있다.

• Consider two categorical variables $X$ and $Y . X$ has $m$ categories, say $1, \ldots, m$ and $Y$ has $k$ categories, $1, \ldots, n$. Let $p_{i j}=P(X=i, Y=j), 1 \leq i \leq m$, $1 \leq j \leq n$.
• Null hypothesis:
  $H_{0}: p_{i j}=p_{i \cdot p} \cdot p_{j}, \quad 1 \leq i \leq m, 1 \leq j \leq k$
  where $p_{i .}=\sum_{j=1}^{n} p_{i j}$ and $p_{\cdot j}=\sum_{i=1}^{m} p_{i j}$. This null hypothesis is equivalent to $X \perp Y$.

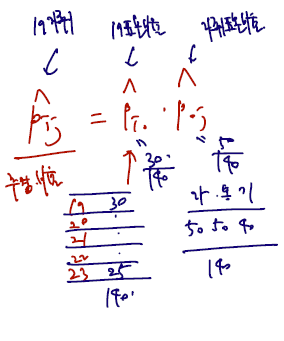
만약 아래와 같은 표가 있다면, pij 를 다음과 같이 채워볼 수 있을 것이다. pij가 19학번 중 자취의 추정비율을 나타낸다고 하자. 그렇다면 19학번 표본비율을 marginal 로 구한다음 곱하고, 자취의 표본 비율을 marginal 로 구한다음 곱해볼 수 있을 것이다. 이렇게 i x j 의 추정비율 칸을 다 채우면 카이제곱 검정을 위한 통계량을 만든다.

• Test statistic: Let $X_{i j}$ be the number of occurrence of the event $(X=i, Y=$ $j)$. Then,
  $Q=\sum_{j=1}^{b} \sum_{i=1}^{a} \frac{\left(X_{i j}-n \widehat{p}_{i j}\right)^{2}}{n \widehat{p}_{i j}}$
  where
  $n=\sum_{j} \sum_{i} X_{i j}, \quad \widehat{p}_{i j}=\widehat{p}_{i} \cdot \widehat{p}_{\cdot j}=\frac{X_{i \cdot}}{n} \frac{X_{\cdot j}}{n}, \quad X_{i \cdot}=\sum_{j} X_{i j}, \quad X_{\cdot j}=\sum_{i} X_{i j}$

역시 여기서도 관찰 도수에서 기대도수를 뺀 값을 구하게 된다. 만약 n=140이고, 19학번 자취가 10명이라면 다음과 같이 쓴다.

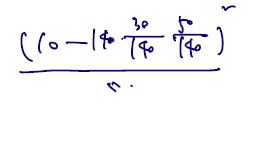
마지막으로 통계량이 다음 카이제곱 분포를 따름을 보이자.

• Asymptotic null distribution:
  $Q \stackrel{H_{0}}{\approx} \chi^{2}(\mathrm{df})$
  where df $=(m k-1)-\{(m-1)+(k-1)\}= (m-1)(k-1)$

역시나 df 는 칸을 채우는 것에 지나지 않는다. 여기서도 마찬가지로, 귀무가설이 맞지 않을 때에서 맞을 때를 빼게 되는데, 맞지 않을 경우 전체 mk 칸 중 1칸만 제외하고 다 구해야 하지만 맞을 경우 독립으로 정의되는 각 칸을 채우기 위해 m-1칸 + n-1칸만 채우고 나머지는 다 곱으로 정의하면 된다.