[Mathematical Statistics] 5. Consistency & Limiting Distributions

5. Consistency & Limiting Distributions (일치성과 극한분포)

5.1 Convergence in probability (확률수렴)
in probability 로 수렴한다, convergence in probability 의 정의가 무엇인지 알아보자.

Definition Let $\left\{X_{n}\right\}$ be a sequence of random variables and let $X$ be a random variable defined on a sample space. We say that $X_{n}$ converges in probability (확률수렴) to $X$ if,

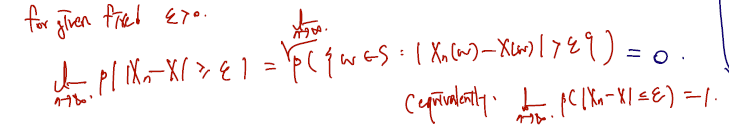
확률수렴의 정의는 다음과 같다.

• 주어진 고정된 엡실론이 0보다 살짝 크다고 할 때
• 확률변수들의 시퀀스 Xn이 X 로 수렴하려면 이들의 차가 앱실론보다 클 확률이 n이 무한대로 가면서 0이 되어야 한다.
• 다시 말해, 이들이 어떤 input w들을 받을 때 차가 앱실론보다 큰 w들이 있는 공간의 확률이 0이어야 한다. (완전히 없다가 아닌, n이 무한대로 감에 따라 없다가 더 맞다.)
• 이와 완전히 같은 표현으로, n이 무한대로 감에 따라 앱실론보다 작을 확률은 1과 같다라고 쓸 수 있다.
  아래의 그림처럼 상상해볼 수도 있다.

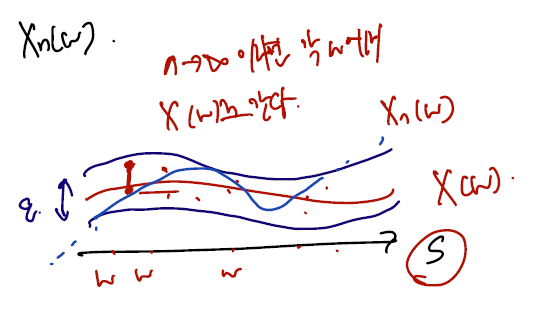
• X(w)와 앱실론만큼의 거리 안으로 Xn(w) 이 다 들어온다는 것이며, 이들의 차이가 앱실론을 벗어나는 영역이 0이 된다는 것이다.
• convergence in probability (확률수렴) 은 convergence in measure (측도수렴) 과 완전히 같은 정의이다.
• 이외에도 수렴에 대한 해석학에서 다루는 내용으로 uniform -> poinwise -> almost sure 수렴이 있고, 앞 순서대로 조건이 더 많고 강한 수렴으로 이해할 수 있다. 여기선 이정도로만 하고 넘어가자.

If so, we write

• Special case: if $X=a$, one can imagine $X_{n} \xrightarrow{P} a$,
• For a non-random sequence $\left\{a_{n}\right\}$ and constant $a, a_{n} \rightarrow a \Longleftrightarrow a_{n} \xrightarrow{P} a$.

이를 토대로 (약한) 대수의 법칙을 써볼 수 있다. 아래를 보면,

Theorem 5.1.1 (Weak Law of Large Numbers). Let $\left\{X_{n}\right\}$ be a sequence of iid random variables having common mean $\mu$ and variance $\sigma^{2}<\infty$. Let $\bar{X}_{n}=$ $n^{-1} \sum_{i=1}^{n} X_{i}$. Then

Proof.

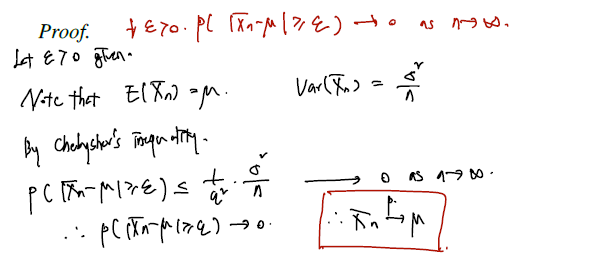
(쳬비셰프 부등식)

대수의 법칙을 쓰기 위해서는 분포의 모평균과 모분산이 값은 unknown 이더라도 finite 로 존재해야 한다. (평균이 존재하지 않는 분포는? -> 코시분포) 그리고 위의 확률 수렴을 쓰면 어렵지 않게 표본평균이 모평균으로 convergence in probabiliy 함을 보일 수 있다. 이에 대한 증명은 보통 부등식으로, 이미 알려진 부등식 내에서 더 큰 항이 0으로 수렴암을 보여서 작은 target 항 또한 0으로 수렴함을 보이는 게 대부분이다.

이어지는 내용은 확률수렴을 사용해서 얻을 수 있는 성질들이다. 아래의 내용을 통칭해 in probability 수렴은 사칙연산과 연속함수 변환에 대해서도 보존된다~ 라고 말할 수 있다. 확률변수와 다른 확률변수를 사칙연산 해도 각각이 수렴하는 확률변수로 수렴한다는 건 꽤나 유용하게 쓰일 수 있는 내용이다.

• additivity
• scala 곱
• continuous function 씌워도 보존
• 두 확률변수 곱에서의 수렴이 있다. 쭉 보자.

Theorem (additivity) Suppose $X_{n} \xrightarrow{P} X$ and $Y_{n} \xrightarrow{P} Y$. Then $X_{n}+Y_{n} \xrightarrow{P} X+Y$.
Proof.

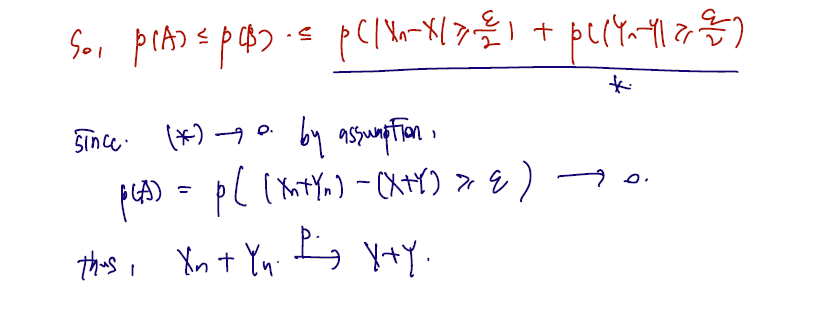
삼각부등식의 내용이 들어가므로 이에 대한 내용을 정리해두도록 하자. ✅

Theorem (scala 곱) Suppose $X_{n} \xrightarrow{P} X$ and $a$ is a constant. Then $a X_{n} \xrightarrow{P} a X$.
Proof. If $a=0$, the result is immediate. Suppose $a \neq 0$. Let $\epsilon>0$. The result follows from these equalities:

and by hypotheses the last term goes to 0 as $n \rightarrow \infty$.

곱해진 스칼라가 절댓값을 빠져나와 부등식 반대로 이동한 경우이다. 이때, 이미 앱실론보다 클 확률이 0이라면 앱실론을 고정된 constant 로 나눈 값은 더 작으므로 더 작아진 이 값보다 클 확률 또한 0이다.

Theorem (연속함수) Suppose $X_{n} \xrightarrow{P}$ a and the real function $g$ is continuous at $a$. Then $g\left(X_{n}\right) \xrightarrow{P} g(a)$.

Proof. Let $\epsilon>0$. Then since $g$ is continuous at $a$, there exists a $\delta>0$ such that if $|x-a|<\delta$, then $|g(x)-g(a)|<\epsilon$. T
이는 continuous 연속함수의 정의를 쓴 것이다. 연속하무의 정의는, input 이 델다보다 작을 경우 output 또한 앱실론보다 작다는 것이며, 이에 대한 대우를 쓰면 다음과 같다.

그리고 정확히 이 식에다 probability 를 씌울 수 있다. 단, 여기서 하나의 부등식이 더 생기는데, 이는 충분조건에 대해 포함관계가 형성되기 때문이다. (output 이 크면 -> input 크다 이므로 output 이 클 확률이 더 작은 요소가 된다.)
Substituting $X_{n}$ for $x$ in the above implication, we obtain

By the hypothesis, the last term goes to 0 as $n \rightarrow \infty$, which gives us the result. (부등식 우변의 probability 가 0으로 수렴하므로 이보다 작은 좌변, continuous 함수를 거친 것 또한 0이 된다.) 이를 활용하면 아래와 같이 다양한 fact 를 자유롭게 사용할 수 있다. sequence Xn 이 상수 a로 수렴할 경우 다음들이 모두 가능하다.

• Examples:
  $\begin{array}{rlll} X_{n}^{2} & \xrightarrow{P} a^{2} & \\ 1 / X_{n} & \xrightarrow{P} 1 / a, & \text { provided } a \neq 0 \\ \sqrt{X_{n}} & \xrightarrow{P} \sqrt{a}, & \text { provided } a \geq 0 . \end{array}$

이를 확장하면 다음과 같은 fact 가 나온다. (증명을 다루진 않고, 자유롭게 쓰자.)

Fact (Continuous mapping theorem ${ }^{1}$ ): In a more advanced course, it is proved that $X_{n} \xrightarrow{P} X$, then $g\left(X_{n}\right) \xrightarrow{P} g(X)$.

• 예시: $X_{n} \xrightarrow{P} X$ 이라면, $X_{n}^2 \xrightarrow{P} X^2$
• $X_{n} \xrightarrow{P} X$ 이라면, $1 / X_{n} \xrightarrow{P} 1 / X$

Theorem (곱) Suppose $X_{n} \xrightarrow{P} X$ and $Y_{n} \xrightarrow{P} Y$. Then $X_{n} Y_{n} \xrightarrow{P} X Y$.
Proof. Using the above results, we have

마지막으로 둘의 곱에 대한 수렴 증명이다. 먼저, 제곱의 수렴은 continuous mappting theorem 에 의한 것이고, 차의 수렴은 -1 scala 변환에 additivity 도 사용된 것이다.

다음은 일치추정량에 대한 정의이다. 일치추정량을 정의할 때도 확률수렴의 개념이 쓰인다.

Definition Let $X$ be a random variable with $\operatorname{cdf} F(x ; \theta), \theta \in \Omega$. Let $X_{1}, \ldots, X_{n}$ be a sample from the distribution of $X$ and let $T_{n}$ denote a statistic. We say $T_{n}$ is a consistent estimator (일치추정량) of $\theta$ if

실제 확률변수 X가 세타를 모수로 하는 cdf 에서 나왔다고 했을 때.. 이들을 관찰한 관찰값 X1 ~ Xn을 가지고 통계량을 만들게 된다. 이렇게 특정 분포의 sample 로부터 나온 값을 가지고 만든 통계량 (e.g. 표본평균, 표본분산, 순서통계량 등)은 그 통계량이 세타로 in probability 수렴할 때 세타에 대한 일치추정량이라 한다. 위의 약한 대수의 법칙을 소개하면서 표본평균이 모평균으로 in probability 수렴함을 보인 것이 그 예시이며, 따라서 표본평균은 모평균의 일치추정량이라 부를 수 있다.

🤔 하나 궁금한 내용은, 일치추정량이란 개념 자체가 unbiased estimator 비편향추정량과 비슷하게 보이는데 서로 다르게 함의하는 부분이 무엇인지 하는 것이다. 1. 일단 표본평균이 모평균의 일치추정량임을 보이기 위해 unbiased estimator 임을 가져다 썼다. 그러니 in probability 수렴은 단순히 표본평균의 기댓값이 모평균이란 것보다 조금 더 강한 sense 인 것 같기도 하고. 2. unbiased estimator 에서 보였던 건 추정량의 기댓값이 모수와 완전히 일치한다 였다면 여기서는 수렴의 개념이다. 그런데 두가지를 모두 확률변수 (또는 constant)로 봤을 때 두 변수 사이의 수렴을 주장하는 것이 변수의 변환 (expectation)보다 더 나아간 주장이므로 강한 주장인가, 싶기도 하다. 이 부분은.. 조금 더 고민해서 나중에 정리하고 싶다.

아래는 모평균의 일치추정량이 되는 표본평균 외에도 sample variance 가 모분산의 일치추정량될 수 있을 지에 대한 증명이다. 마찬가지로, n이 무한대로 갈 때 표본분산이 모분산으로 수렴함을 보이면 된다.

Example (Sample variance) Let $X_{1}, \ldots, X_{n}$ denote a random sample from a distribution with mean $\mu$ and variance $\sigma^{2}$. Recall that the sample variance is defined by $\frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}$. Assume further that $E\left[X_{1}^{4}\right]<\infty$, so that $\operatorname{Var}\left(S^{2}\right)<\infty$. Show that $S^{2}$ is a consistent estimator of $\sigma^{2}$.

• 확률변수들은 모평균, 모분산이 finite 로 존재하는 분포에서 추출되었고,
• 표본분산 S^2 은 원래 계산하는 대로 계산한다고 하자.
• WLLN에서 필요한 건 $E\left[X_{1}^{2}\right]<\infty$ 이었고, 이번엔 4승도 존재한다고 가정하자.

(proof)

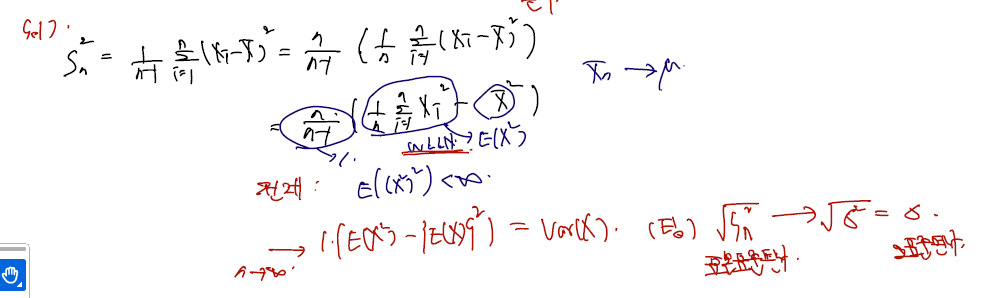
표본분산의 정의로부터 시작하여 각각 WLLN과 in probability 수렴을 쓰면 n이 무한대로 갈 때 모분산으로 수렴함을 보일 수 있다. 각각 $E(X^2)$ 로 만들 때 WLLN 가 쓰이고, $E(\bar{X})^2$ 를 보일때 $\bar{X}$ 가 모평균 뮤로 in probability 수렴함을 쓴다. 이를 통해 n이 무한대로 가면 모분산을 계산하는 form 임을 보일 수 있다. 덤으로, 표본표준편차 또한 모표준편차로 in probability 수렴하게 된다.