[Mathematical Statistics] 5.2 Convergence in distribution

박경민·2024년 9월 30일

[Mathematical Statistics]

목록 보기

17/24

Review (확률수렴)

5.1 절에서는 확률수렴의 정의와 확률수렴을 사용해서 보일 수 있는 것들을 다뤘다. 확률수렴의 정의는 다음과 같다.

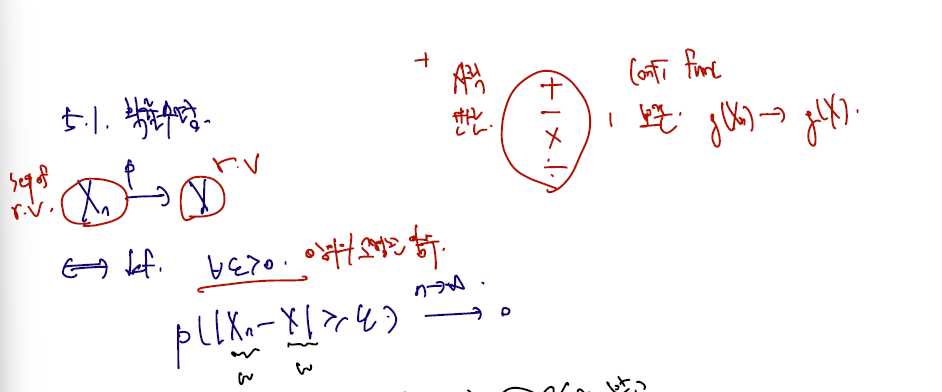
sequence of random variable 이 random variable 로 convergence in probability 한다는 것은.. 임의의 고정된 양수 엡실론에 대해, Xn 과 X 각 확률변수 차가 앱실론 밖으로 나갈 확률이 n이 무한대로 갈 때 0이라는 것이다. 이때 Xn, X 는 확률변수이므로 '규칙', 즉 sample space 의 원소인 w을 input 으로 받고 output 을 실수 전체 집합으로 하는 규칙 자체를 말한다. 따라서 둘 output 의 차이가 엡실론보다 커지는 input 집합의 확률이 0으로 간다, 와 같은 notation 이다.

이러한 확률 수렴은 두 확률변수가 있을 때 이들 사이의 사칙 연산, continuous function 변환에도 보존되었다. (각각의 수렴이 결과의 수렴으로 보존되었다.) 그리고 이를 바탕으로 in probability 수렴이 작동하는 예시를 확인했다. n이 무한대로 갈 때 표본을 가지고 얻은 추정량이 모수로 in probability 수렴함을 보이고, 이렇게 확률 수렴하는 추정량을 일치추정량이라 하였다. (이를 표본평균이 모평균에 대해 확률수렴함을, 표본분산/표본표준편차가 모분산/모표준편차에 대해 수렴함을 증명함으로써 예제를 풀었다.)

이어지는 내용은 in distribution 수렴, 분포 수렴이다. 분포 수렴의 정의와 성질부터 (분포수렴은 일반적으로 사칙연산이 보존되지 않는 것이 trivial 한 성질이나 non-trivial 한 counter example 들도 챙겨야 한다.) 분포수렴 & 확률수렴의 관계를 다뤄보자.

5.2 Convergence in distribution

Convergence in distribution (분포수렴)

Definition. Let $\left\{X_{n}\right\}$ be a sequence of random variables and let $X$ be a random variable. Let $F_{X_{n}}$ and $F_{X}$ be, respectively, the cdfs of $X_{n}$ and $X$ . Let $C\left(F_{X}\right)$ denote the set of all points where $F_{X}$ is continuous. We say that $X_{n}$ converges in distribution (분포수렴) to $X$ if

여기서도 마찬가지로 $X_n$ 은 확률변수의 sequnce 이고, $X$ 는 확률변수이다. 그리고 이들 각각의 cdf 가 존재한다고 하자. (분포수렴이므로 둘 간의 cdf 가 수렴한다고 직관적으로 이해하자.)
수렴의 범위는 $X_n$ 이 아닌 $X$ 의 cdf 인 $F_x$ 가 연속인 점에서만, 이다. 그리고 이 점들을 $C(F_x)$ 라 한다. 아래의 예제들에서는 cdf 가 한 점에서 연속이 아닌 분포들이 등장한다. 예컨대 아래 그림과 같은 $F_x$ 가 있으면 불연속인 점들을 제외한 연속인 점들에서만 수렴함을 보이면 된다.

정의는 다음과 같고, 이 notation 을 통해 여러가지 확률변수들이 분포 수렴함을 보일 것이다. $X_n$ 의 cdf 가 n이 무한대로 갈 때 임의의 고정 x점 (x는 $F_x$ 가 연속인 점들만)에서 $X$ 의 cdf 로 수렴함을 보이면 된다.

정의 자체가 어렵게 느껴질 수 있으나 익숙하지 않아서고, 이름부터 분포 수렴이니 두 확률변수 사이의 cdf 분포들이 n이 무한대로 갈 때 수렴한다고 보면 된다. (X의 cdf 가 연속인 점에서만 고려하는 이유는 아래에 이어진다.)

이를 다음과 같이 denote 한다.

We denote this convergence by

X_{n} \xrightarrow{D} X .

이때, target 이 되는 X 확률변수가 확실히 어떤 분포 (여기선 N(0,1)이라 해보자.) 를 따르고 있다면 확률변수 자리에 그냥 분포로 수렴한다고 적어도 된다.

X_{n} \xrightarrow{D} N(0,1) .

notation 상 중요한 것은 normal(0,1) 의 pdf 를 이상상하면 안되고 cdf 로 수렴함을 명심해야 할 것이다. 예컨대 $X_{n} \xrightarrow{D} 0$ 과 같은 notation 이 등장할 경우도 후에 있는데, 이는 0으로 수렴한다는 것이 아니라 0에서 확률이 1이고 나머지가 0인 mass 를 가지는 cdf 로 수렴한다는 notation 이다. 따라서 이런 노테이션이 있다면 0의 좌극한으로는 0으로 수렴하고, 우극한과 함숫값은 1일 것이다.

그렇다면 왜 X가 연속인 $C(F_X)$ 에서만 수렴함을 고려할까? 아래의 예제를 보자.

Example. (Motivation for considering only points of continuity of $X$ ) Let $X_{n} \equiv$ $1 / n$ and $X \equiv 0$ . Observe that

$X_{n} \xrightarrow{D} X$ by definition.

Xn은 1/n 인 값만 가지는 확률변수이고, X는 0인 값만 가지는 확률변수이다. 이들의 cdf 를 각각 그려보면 다음과 같다.

따라서 $C(F_x)$ = $R-{0}$ 인 집합에서만 정의된다. 이 cdf 를 식으로 각각 쓰면 다음과 같다.

둘 다 우극한에서 함숫값도 포함이 된다.

x가 연속인 구간에서만 이제 증명하자.

x가 0보다 클 때는 n이 무한대로 갈 때 $F_{x_n}(x)$ 는 1로 수렴한다. 따라서 $F_x(x)$ 와 같은 값을 가진다.
x가 0보다 작을 때는 n이 무한대로 갈 때 $F_{x_n}(x)$ 는 0으로 수렴하고, 따라서 $F_x(x)$ 와 같은 값을 가진다.
만약 X가 연속인 구간이 아닌 x= 0인 지점을 정확히 찍으면, $F_{x_n}(0)$ 은 0일 것이고 $F_x(x)$ =1 이므로 일치하지 않는다. 따라서 이 점은 분포 수렴에선 다루지 않는다.

아래의 이어지는 예시는 Xn 이 N(0, 1/n) 을 따를 떄 n을 무한대로 보내면 cdf 가 직관적으로 생각하는 분포로 분포 수렴할 지에 대한 증명이다. 그림을 보자.

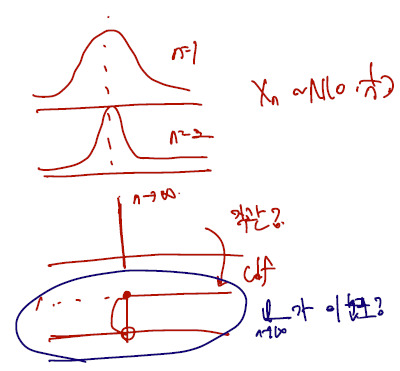
n = 1일 땐 분산이 1인 정규분포이므로 잘 아는 그래프지만 n이 커질 수록 0을 벗어나는 확률들이 줄어들고 결국은 n이 무한대로 가면 0에서만 1의 mass 를 가지는 분폭 될 것이다. 그럼 N(0, 1/n) 을 따르는 Xn을 무한대로 보내면 가장 아래의 cdf 로 수렴할까? 직접 계산하면 된다!

\begin{aligned} F_{X_{n}}(x) & =\int_{-\infty}^{x} \frac{1}{\sqrt{1 / n} \sqrt{2 \pi}} e^{-n w^{2} / 2} d w \\ & =\int_{-\infty}^{\sqrt{n} x} \frac{1}{2 \pi} e^{-v^{2} / 2} d v \end{aligned}

by changing variable $v=\sqrt{n} w$ . Find the limiting distribution of $X_{n}$ .

여기서 위끝의 x에 음수를 대입하면 (x가 음수라면) n이 무한대로 가므로 -무한대부터 -무한대까지 해당 pdf 를 적분하는 꼴이 된다. pdf 는 N(0,1)이므로 이를 다음 범위에서 적분하더라도 0이고..

위끝의 x에 양수를 대입하면 -무한대부터 +무한대까지 범위에서 N(0,1) 의 적분이므로 1이 된다. x=0을 대입해 계산하면 1/2이 뜬다.따라서 다음과 같이 쓸 수 있다.

(sol)

\therefore \lim _{x \rightarrow \infty} F_{X_{n}}(x)= \begin{cases}0, & x<0 \\ 1 / 2, & x=0 \\ 1, & x>0\end{cases}

이 limit 가 우리가 상상한 직관적인 cdf 로 수렴하는지만 보면 된다. 아래의 cdf 는 임의로 취한 것인데

So, take

F(x)= \begin{cases}0, & x<0 \\ 1, & x \geq 0\end{cases}

이다. 따라서 이 확률변수 Xn은 바로 위 $F(x)$ 를 cdf 로 가지는 X로 분포 수렴, 다음과 같이 쓸 수 있다.

X_{n} \xrightarrow{D} X .

X_{n} \xrightarrow{D} 0 .

0으로 arrow 가 나타내어진 것은 Xn 이 X: 0에 mass 가 집중된 (확률이 1인) 분포를 cdf 로 하는 그 cdf 에 분포수렴한다, 를 뜻한다.

Example Let $X_{1}, \cdots, X_{n}$ be r.s. from $U(0, \theta)$ , and let $Z_{n}=n\left(\theta-Y_{n}\right)$ , where $Y_{n}=\max \left(X_{1}, \cdots, X_{n}\right)$ . Find the limiting distribution of $Z_{n}$ .

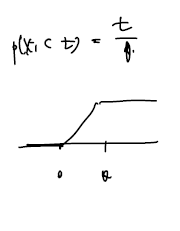
uniform distribution 을 가지는 X의 cdf 를 그려보면 다음과 같다.

문제는 정의된 Zn이 어느분포로 수렴될 지를 묻고 있고, Zn 자체를 과도하게 해석하기 보단 일단 집어넣으면 풀린다.

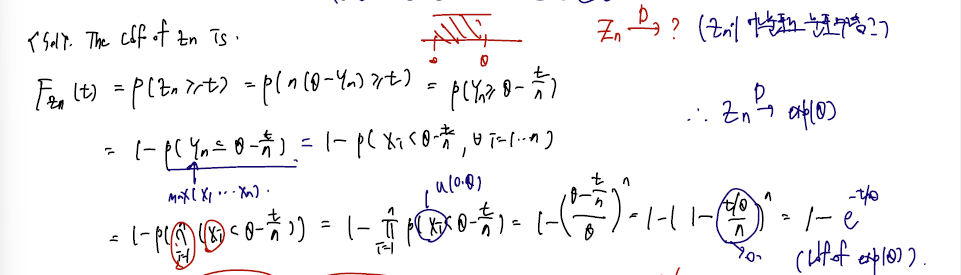
보통은 바로 limit 을 붙이기보단 Zn의 cdf 를 쓰고, 구한 값에 limit n을 무한대로 보내면 된다.
cdf 의 전형적인 notation 을 쓰고.. Zn 대신 Yn을 포함한 주어진 값을 집어넣자.
Yn은 X1.. Xn 까지 돌며 가장 큰 값이므로 이들 간의 intersection 확률을 곱하면 된다. (그럼 X1 ~ Xn 중 가장 큰 값이 Yn이 되며 딱 이때의 확률만 구해질 수 있을 것이다.)
각 Xi가 독립이므로 intersection 은 곱으로 풀 수 있고..
위 그림에서 Xi 가 t보다 작을 때의 값에서 t를 갈아끼우면 된다.
이를 풀고, n을 무한대로 보내면 (Zn의 cdf 를 무한대로 보내면) exponential 의 cdf가 튀어나온다. 따라서 Zn은 exponential 분포로 분포수렴한다.

Z_{n} \xrightarrow{D} exp(\theta).

이어지는 내용은 분포 수렴과 다른 수렴들 간의 관계이다. 분포 수렴이 다른 수렴을 implies 하는지/못하는지, 다른 수렴이 분포 수렴을 implies 하는지/못하는지에 대한 것이고, 특히나 이전 절에서 다룬 확률수렴과의 관계가 주다.

Theorem $X_{n} \xrightarrow{P} X \Rightarrow X_{n} \xrightarrow{D} X$ , i.e., convergence in probability implies convergence in distribution.

첫번째로 두 확률 변수가 확률수렴의 관계에 있다는 것이 분포 수렴을 implies 한다는 것. 이에 대한 증명은 다음과 같다.

Proof. Let $x$ be a point of continuity of $F_{X}(x)$ . For every $\epsilon>0$ ,

\begin{aligned} F_{X_{n}}(x) & =P\left[X_{n} \leq x\right] \\ & =P\left[\left\{X_{n} \leq x\right\} \cap\left\{\left|X_{n}-X\right|<\epsilon\right\}\right]+P\left[\left\{X_{n} \leq x\right\} \cap\left\{\left|X_{n}-X\right| \geq \epsilon\right\}\right] \\ & \leq P[X \leq x+\epsilon]+P\left[\left|X_{n}-X\right| \geq \epsilon\right] \end{aligned}

Xn의 cdf 에 대한 upper bound 를 표시하기 위해 여기에 sup.lim 을 씌울 것이다. 그러면 n이 무한대로 가면서 마지막 term 이 0으로 날아가고 upper bound 를 할 수 있게 된다.

위 식에 처음부터 아래를 넣어 lower bound 를 구한다.

P\left[X_{n}>x\right] \leq P[X \geq x-\epsilon]+P\left[\left|X_{n}-X\right| \geq \epsilon\right]

역시나 식의 전개는 위에서와 비슷한 idea 를 쓰고, (P(A) 풀어내는데서 약간의 idea 가 필요하고, 부등식 전개는 그냥 하면 된다.) 각각 두 개의 부등식에 대한 확률이 나온다면 1- cdf 식으로 바꿔서 아래의 식을 얻을 수 있다.

Hence

\underline{\lim }_{n \rightarrow \infty} F_{X_{n}}(x) \geq F_{X}(x-\epsilon)

이는 inf.lim 을 씌운 lower bound 이다. 따라서 Xn의 upper bound, lower bound 를 종합하면 다음과 같다.

Using a relationship between $\bar{\lim }$ and $\underline{\lim }$ , it follows from (5.2.5) and (5.2.6) that

F_{X}(x-\epsilon) \leq \underline{\lim }_{n \rightarrow \infty} F_{X_{n}}(x) \leq \bar{\lim}_{n \rightarrow \infty} F_{X_{n}}(x) \leq F_{X}(x+\epsilon)

이는 임의의 양수 엡실론에 대해 성립해야 하므로 부등식 왼쪽 끝과 오른쪽 끝에 limit 을 취하여 이들이 같음을 보이고, 따라서 limit $F_{X_n}(x)$ 이 존재함을 보일 수 있다.

그러나 아래에 이어지는 내용은 이 statement 의 역은 성립하지 않음을 보여준다.

Remark. The converse of Theorem 5.2.1 is not true in general. i.e., convergence in distribution DOES NOT impliy convergence in probability.

(Counterexample) Let $X$ be a continuous random variable with a pdf $f_{X}(x)$ that is symmetric about 0 ; i.e., $f_{X}(-x)=f_{X}(x)$ . Then it is easy to show that the density of the random variable $-X$ is also $f_{X}(x)$ . Thus, $X$ and $-X$ have the same distributions. Define the sequence of random variables $X_{n}$ as

만약 sequence of Xn을 n이 홀수일 때와 짝수일 때로 다르게 주고, 홀수일 때 X를, 짝수일 때 -X를 취하도록 한다고 해보자. 그리고 symmetric 한 분포로 각각이 Xn와 X 각각이 N(0,1) 을 따른다고 한 분포를 찍어보자.
그렇다면 Clearly, $F_{X_{n}}(x)=F_{X}(x)$ for all $x$ in the support of $X$ 일 것이다. cdf 가 같으니까 이를 쉽게 보일 수 있다! 따라서 $X_{n} \xrightarrow{D} X$ . 분포수렴은 되지만..
확률 수렴이 되는지를 아래 정의에 따라 써볼 수 있다. (By the definition of convergence in probability,)
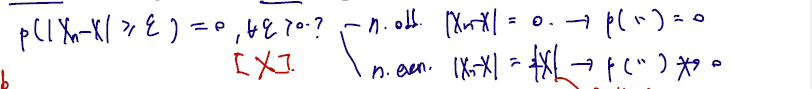
n이 odd 라면 $p(0 >= \epsilon)$ 이므로, 엡실론은 임의의 양수로만 정의되므로 0인 반면에 n이 even 이라면 2|X| 가 된다. 이미 X는 N(0,1) 분포를 따르고 있으므로, 이 값이 앱실론보다 큼은 자명하다.
따라서 $X_{n} \nrightarrow X$ in probability. 라고 쓸 수 있다. 이처럼 분포 수렴은 확률수렴을 imply 하지 않는다.

아래의 두 가지는 proof 를 다루진 않을 것이나 fact 로 잘 알아두자.

Theorem* $X_{n} \xrightarrow{D} X$ , $g:$ continuous function. $\Longrightarrow g\left(X_{n}\right) \xrightarrow{D} g(X)$ .

e.g. If $X_{n} \xrightarrow{D} N(0,1)$ , then $X_{n}^{2} \xrightarrow{D} \chi^{2}(1)$ .

사칙연산에 대해 보존이 되지 않는 분포 수렴이지만 continuous function 에 대해선 보존이 된다. 예컨대, Xn 이 N(0,1) 을 따르는 X로 수렴한다면, Xn의 제곱 또한 X의 제곱의 분포, 카이제곱(1)의 분포로 수렴할 것이다. 마찬가지로, 분포수렴이라면, 연속함수를 거쳐 나온 어떤 Xn 변수가 같은 함수를 거쳐나온 X가 따르는 분포로 수렴할 것임을 알 수 있다.

Theorem (Slutzky's Theorem). Let $X_{n}, X, A_{n}$ , and $B_{n}$ be random variables and let $a$ and $b$ be constants. If $X_{n} \xrightarrow{D} X, A_{n} \xrightarrow{P} a$ , and $B_{n} \xrightarrow{P} b$ , then

A_{n}+B_{n} X_{n} \xrightarrow{D} a+b X .

분포 수렴에서 사칙연산은 안되지만 상수배와 더하기의 경우에 그 상수배해주는 변수, 더해지는 변수가 확률변수가 아닌 상수로 수렴한다면 수렴이 가능하다. 헷갈릴 수 있으므로 다시 구분하자면

Xn, An, Bn 은 모두 확률변수이고
이들이 수렴하는 건 X는 확률변수, a는 constant, b도 constant 이다.

여기까지 알았다면 다음 2가지 사실을 더 보일 수 있다.

e.g. Consider $T=\frac{\bar{X}-\mu}{S / \sqrt{n}}$ .

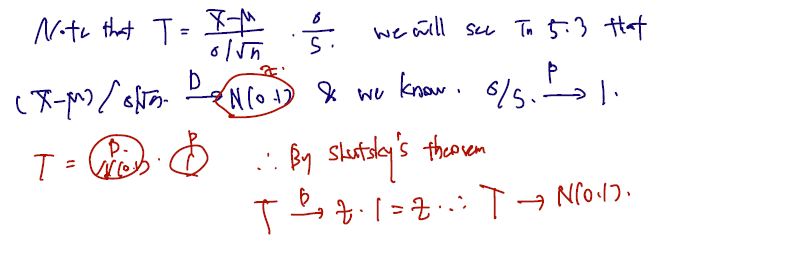
주어진 통계량이 왜 N(0,1) 을 따르는지 (완전한 증명은 아니지만) Slustsky's theorem 을 통해 확인할 수 있다. 표본분산을 모분산으로 갈아끼고 모분산을 표본분산으로 나눈 것을 곱하는 식으로 식을 변형하자. 모분산을 포함한 앞쪽은 N(0,1) 로 분포 수렴한다고 하자. (이에 대한 정확한 증명은 5.3 절에서 다룬다.) 그리고 모분산을 모표준편차로 나눈 것은 in probability 1로 수렴함을 이전에 보였다. 따라서 통계량 T는 Zn 이 normal (0,1) 을 따르는 Z로 분포수렴하는 변수에, An 이 a로 in probability 수렴하는 것을 곱한 것과 같다.

(1) Z_{n} \xrightarrow{D} Z (Z는 N(0,1)을 따름)

(2) A_{n} \xrightarrow{D} a (a는 constant)

(3) Z_{n} x A_{n} \xrightarrow{D} aZ

여기서 (1) & (2) -> 3으로 넘어올 떄 Slutzky's Theorem이 사용되었다.

Remark. $X_{n} \xrightarrow{D} X \& Y_{n} \xrightarrow{D} Y$ does not imply $X_{n}+Y_{n} \xrightarrow{D} X+Y$ nor $X_{n} Y_{n} \xrightarrow{D}$ $X Y$ .

각 확률변수가 분포 수렴한다고 해도 이들을 더하거나 곱한 것이 수렴하진 않는다. 반례는 두 seqence $X_n$ , $Y_n$ 를 N(0,1) 을 따르도록 두고, $X$ 은 N(0,1) 을 따르도록 두되 Y := -X로 주면 반례가 된다.

(Counterexample for $X_{n}+Y_{n} \xrightarrow{D} X+Y$ )

마지막 N(0,2)가 0이 아님에 대한 건 N(0,2)의 cdf 에 limit 을 취하고, 이것이 0이 아님을 보이면 된다.

박경민

Mathematics, Algorithm, and IDEA for AI research🦖

이전 포스트

[Mathematical Statistics] 5. Consistency & Limiting Distributions

다음 포스트

[Mathematical Statistics] 5.2 Convergence in distribution