[Mathematical Statistics] 5.3 Central Limit Theorem

5.3 Central Limit Theorem (중심극한정리)

중심극한 정리는 확률, 통계 전반에 걸쳐 잘 알려지고 자주 사용되는 fact 로, 이미 지난 절들에서 이를 활용해서 예제를 풀었다. 그러나 직접적인 증명은 다루지 않았는데.. 이제 증명을 할 수 있는 적절한 다른 fact 들을 알아둔 상태다. 들어가보자!

Theorem (Central Limit Theorem, 중심극한정리). Let $X_{1}, \cdots, X_{n}$ be a r.s. from a random variable X with distribution of mean $\mu$, variance $\sigma^{2}$. Then, $\sqrt{n}(\bar{X}-\mu) / \sigma \xrightarrow{D} N(0,1)$.

말이 좀 어려울 수 있지만 표본평균이 다음을 따를 때 이를 잘 정리한 (잘 알고있는) 통계량 Yn이 N(0,1) 을 따르는 것에 대한 증명이다. 그러나 여기서 또한 asymptactic 이 아니라 어떤 mode 로 따르는지도 보일 수 있는데, 통계량 Yn은 N(0,1) 을 in probability convergence 함을 증명해 보일 것이다.

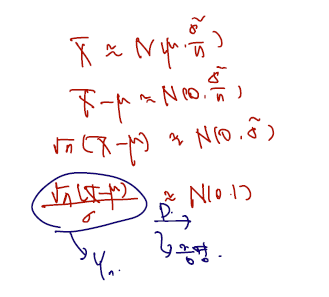
(proof)

이에 대한 증명을 위해 통계량 Yn의 mgf 를 구한 후 이것이 n이 무한대로 가면 결국 N(0,1)의 mgf 로 수렴한다는 것을 보일 것이다. 단, 이를 위해 기존 mgf 를 '살짝 변형' 한 형태의 mgf 를 쓸 것이다. small mgf 로 쓸 것이며, 확률변수 X가 아닌 $X-\mu$ 의 mgf 를 쓰면 다음과 같다.

also exists for $-h<t<h$.

• 0을 포함하는 개구간으로 t가 존재하는 범위가 변하지 않는 까닭은 범위 t가 $X-\mu$ 에는 depend 하지 않기 때문이다.
• it must follow that $m(0)=1, m^{\prime}(0)=E(X-\mu)=0$, and $m^{\prime \prime}(0)=E\left[(X-\mu)^{2}\right]=\sigma^{2}$.
• By Taylor's formula, there exists a number $\xi$ between 0 and $t$ such that (테일러 1차 전개 이용, m(t) at t=0, 0과 t사이에 $\xi$ 가 있다고 하면 다음과 같다.)

• m(0) = 1이고, m'(0) 은 0이니 다음과 같다.
• $\xi$ 가 0으로 다가감에 따라 $m^{\prime \prime}(0)=E\left[(X-\mu)^{2}\right]=\sigma^{2}$ 이므로 여기서 $\sigma^{2} t^{2} / 2$ 를 더하고 빼여 아래와 같이 쓴다.

이것이 $X-\mu$ 의 mgf 이다. 이건 잠깐 멈춰두고, 원래 확률변수 Yn으로 돌아가 이의 mgf 를 구해서 돌아오자.

[1] $Y_n$ 의 mgf 를 M에 대해 쓰기.

[2] $X_i$'s are independent, $X_i$'s are identically distributed 이용, small m mgf form으로 정리

[3] t대신 $\frac{t}{\sigma \sqrt{n}}$ 가 들어가므로 이에 대해 범위 수정.

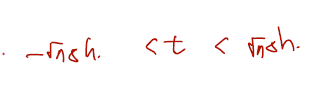
이제 equation (1)에서 구해둔 식에 t대신에 $\frac{t}{\sigma \sqrt{n}}$를 치환해서 넣어주면 다음을 얻을 수 있다.

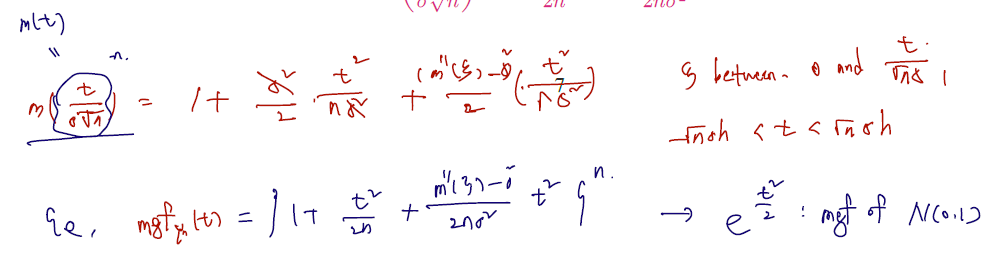
그런데 여기서 rigorous 하게 따져야 할 것이 어떤 상황에서 mgf of Yn이 mgf of N(0,1)로 수렴하냐는 것이다. n이 무한대로 갈 때 mgf of Yn (분포의 극한)이 mgf of N(0,1) 로 수렴한다는 계산이 필요한데, 이것이 convergence in distribution 의 정의였다.

그런데 이를 위해 mgf of Yn의 마지막 항이 o(n)으로 가야한다는 조건이 필요하다. 아래를 보자.

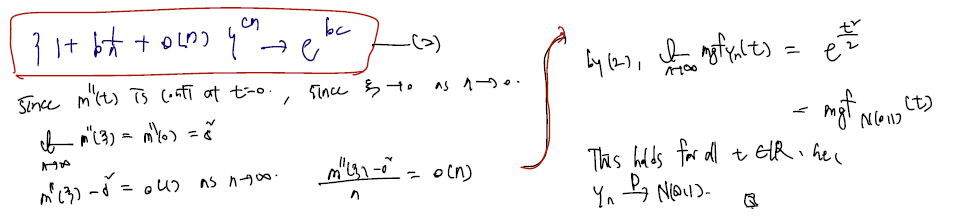
• n이 무한대로 가면 $m''(\xi)$ 도 sigma 제곱으로 갔고.. 이를 차로 표현해서 o(1), 으로 나눠줘서 o(n) 으로 표시할 수도 있다.
• 현재 있는 form 은 n에 depend 하므로 o(n)이라 할 수 있고
• 이때의 경우 $e^{bc}$가 가능하다.

따라서 증명이 되었다!

이를 이용하면 아래의 예제들이 풀린다.
Example Let $X_{1}, \cdots, X_{n}$ be a r.s. from $B(1, p)$ with $0<p<1$. Then, by CLT, $\sqrt{n}(\bar{X}-p) / \sqrt{p(1-p)} \xrightarrow{D} N(0,1)$.

Example (Variance stabilizing transformation). The limiting distribution above depends on the unknown parameter $p$. Find a transform $h(\cdot): \mathbb{R} \rightarrow \mathbb{R}$ such that $\sqrt{n}(h(\bar{X})-h(p)) \rightarrow N\left(0, c^{2}\right)$ where $c$ is a global constant that does not depend on the true parameter.

이 예제의 핵심은 위의 예제로부터 $\sqrt{n}(\bar{X}-p) \xrightarrow{D} N(0,p(1-p))$가 자명할 때.. (분산 term 으로 들어갈 땐 제곱해서 들어간다) 수렴하는 p(1-p) 가 여전히 unknown paramter p에 depend 하는 것이 마음에 들지 않는다는 것이다. 적절한 $h()$ 함수가 존재하여 이들을 각각 변환하면 $c^2$ constant 로 수렴하게 만드는 h함수가 뭘까? 하는 질문이다.

$(sol)$

• linear 든, non-linear 변환이든 nomral 을 따르게 해주는 델타 method 를 쓰면 된다. 이때 분산 term에 transformation 이 제곱되어 들어간다.
• 여기서도 그럼 마찬가지로.. $p(1-p)h'(p)^2$ 로 표시할 수 있고,
• 이것을 c 제곱으로 두고 적분하면 적절히 constant 가 되도록 하는 h(p) 함수를 쓸 수 있게 된다.

This kind of transformation called the variance stabilizing transformation.