
Bayes' rule
베이즈 이론이라 부르는 확률에서 중요한 개념을 다시 정리해보자! Bayes' rule 에서 가장 중요한 것은, 기존의 믿음에 대한 확률을 새로운 정보를 통해 업데이트하는 것에 있다.

베이즈 확률을 한눈에 정리하면 다음과 같다. P(A|B) 를 계산하는데는 각각의 확률 (P(a)와 P(b), 그리고 conditional probability P(B|A) 가 필요하다.)
미리 말하지만, 여기서 업데이트의 대상이 되는 것은 기존의 믿음 P(A) 이다. 따라서 기존의 믿음 정보 P(A)가 이미 있고, P(B)와 P(B|A) 가 있을 때 비로소 업데이트가 가능함을 염두에 두자.
초콜릿 확률
유명한 예시 중 하나가 다음과 같은 예시이다.
철수는 평소에 영희를 마음에 두고 있었는데, 철수의 생일날 철수는 영희로부터 초콜릿을 받았다. 철수는 영희의 마음이 궁금해지기 시작했고, 초콜릿을 줬을 때 호감이 있을 확률을 계산하기로 한다. (이는 분명 철수가 기존에 생각하던 '영희가 나에게 관심이 있을까..?'하는 확률과는 다를 것이다.)
기본적으로 철수는 기존에 영희가 자신을 50% 확률로 좋아하고 있다고 가정한다. 따라서
- P(A): 영희가 철수에게 호감이 있을 확률 = 0.5
- P(B): 초콜릿을 줄 확률
과 같이 정리할 수 있다.
필요한 정보는 호감이 있을 때 초콜릿을 줄 확률이다. 누군가 호감이 있을 때 초콜릿을 줄 확률을 40%, 초콜릿을 줬지만 예의상 줬을 확률을 30% 라 하자. 그럼 다음과 같이 정리가 가능하다.

합이 1이 되는 쌍은 각각 결과가 반대일 경우이다. 호감이 있지만 초콜릿을 주지 않은 경우 (= 0.6), 호감도 없고, 초콜릿도 주지 않은 경우 (=0.7) 이 있다.

이제 P(A) 철수는 영희가 본인에게 호감이 있을지 여부부터 시작하여 본인이 초콜릿을 받았을 때 호감이 있을 확률을 계산한다. 표로 정리하면 아래와 같다.
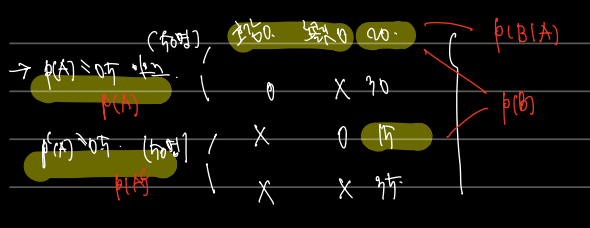
직관적으로 생각할 때 초콜릿을 받은 35 중, 호감이 있다는 20 을 고르면 되므로 20/35 가 될 것이다. 이 계산은 어떻게 가능했나?
필요한 건 노란색 정보들이다.
- 영희가 철수에게 호감이 있을 확률 P(A) = 0.5
- 철수가 초콜릿을 받을 확률 P(B) = 0.35
- 호감이 있을 때 초콜릿을 줄 확률 P(B|A) = 0.4
따라서 식으로 정리하면 다음과 같다.

계산된 결과로 0.57, 즉 초콜릿을 받았을 때(B) 호감이(A) 있을 확률은 0.57 이다.
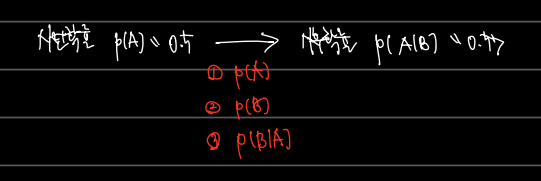
계산된 결과의 의의는 사전 확률을 새롭게 얻은 정보로 사후 확률로 업데이트를 한다는 데 있다. 철수가 가지고 있던 사전 확률은 단순히 영희가 본인을 좋아할 지 모르는 0.5 의 확률 P(A) 뿐이었는데, 2) 초콜릿을 받을 확률과 3) 호감이 있을 때 초콜릿을 줄 확률을 가지고 초콜릿을 받았을 때 호감이 있을 확률이라는 사후 확률로 업데이트를 했다. 0.5에서 0.57로 높아졌으니, 철수 입장에선 호재겠다!