[NLP] PPL derivation

Language model perplexity

정의를 보면 다음과 같다. 해당 perplexity 는 모델의 성능지표로 쓰여 낮을수록 좋다고 여겨지는데, 왜 그런걸까? derivation 을 이해하려면 먼저 Entropy 에 대한 이해부터 시작해야 한다.

1) Entropy

Entropy 란 정보 이론에서 정보가 가지는 정보의 크기를 뜻한다. 값이 클수록 정보가 크고, 컴퓨터 입장에서도 정보를 표현/기억하기 위해 드는 크기가 큼을 뜻한다. Entropy 는 위와 같은 식으로 표시되는데, 쉬운 에로 동전(coin)을 던질 때 앞면, 뒷면(H, T) 이 나올 수 있을 때의 정보의 크기는 다음과 같다.

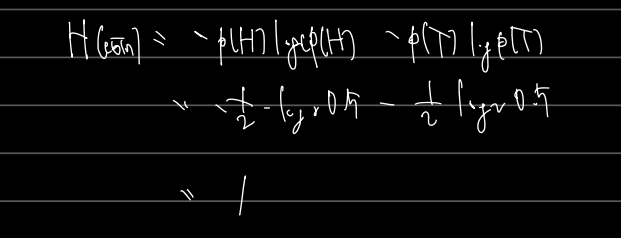
별다른 조건의 개입없이 동전의 앞면과 뒷면을 던질 때 확률이 0.5 라고 하면 Entropy 는 1과 같은 작은 값을 갖게된다. 수가 커질수록, 2진수로 표현해야 하는 컴퓨터 입장에서 드는 bits 의 수도 많아짐을 알고 넘어가자.

2) Entropy of Language

그렇다면 언어(L) 그 자체의 엔트로피를 어떻게 계산할까? 언어는 동전처럼 앞, 뒤로 단순히 계산할 수 있는 확률값이 아닐 것이다. 수많은 문장과 수많은 단어가 있는데 어떻게 이를 계산할까? 일단 주어진 문장에서의 entropy 만 계산한다고 하자.

문장의 entropy

문장 길이가 n일 때, 문장의 entropy 는 다음과 같이 계산될 수 있다. p(w)는 얼마가 될지 모르지만 전체 언어 L에서 단어 w가 등장할 확률이다.

Entropy rate
그러나 위의 계산은 처음 동전 던지기에서 구한 엔트로피와 달리 문장 길이에 따라 값이 달라진다. (길이가 길어질수록 정보가 많아질 것이다.) 따라서 이를 문장 길이로 나눠주자. 이를 Entropy rate, 즉 엔트로피 비율이라 한다.

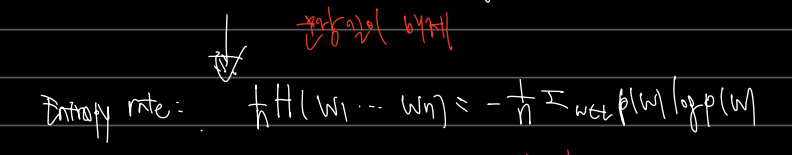
lg. entropy
다음으로는 언어에 대한 엔트로피 계산이다. 일단 아래와 같이 표현이 가능하다. 문장의 길이를 늘려 무한대만큼 긴 문장이 있으면 그 언어의 엔트로피 계산이 가능해질 것이다. 문제는 p(w)이다. L에서 단어 w 의 등장확률 p(w)를 어떻게 정의, 근사할 것인가?

3) Stationary and ergonic process

여기서 중요한 가정이, 언어가 stationary, ergonic 한 경우, 언어에 대한 엔트로피는 다음과 같이 계산 가능하다는 것이다.

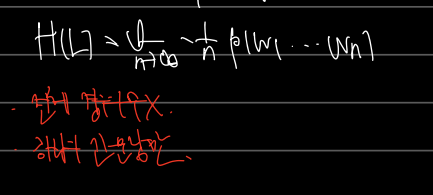
언어의 엔트로피를 구할 때 전체 경우의 수가 아닌 하나의 긴 문장만 가정하는 것이다. 이때 stationary? Ergonic 하다는 것은 무얼까?

Language model 즉 n-gram 의 경우 확률이 앞의 단어에 주로 의존하지 시간에 의존하지 않다는 것이다. 물론 시간에 따라 변화하긴 하지만 그렇기에 Stationary, Ergonic 을 보고 그렇다면 시간에 따른 변화는 미미하다고 여기는 것이다.

4) Cross Entropy

Cross Entropy 는 이전에 문제되었던 것, 언어에 대한 Entropy 를 구하려고 하는데 true probability 를 알지 못할 때 등장하는 것이다. Cross Entropy 로 위 문제를 근사하여 해결해보자!

True probability (그러니까 실세계의 확률) 을 p라하고, model probability (모델 에측확률)를 m이라 할 때, Cross entropy H(p,m) 은 다음과 같다.

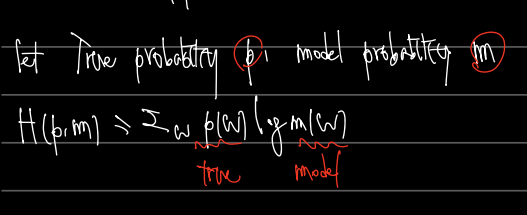
따라서 True probability 는 Cross Entropy H(p,m) 보다 항상 작거나 같다. 모델의 예측과 true prob은 언제나 차이가 있을 수 있기 때문이다.

모델링의 관점에서 얼마나 정확한 모델인지는 위 값이 작은 것이 좋다고 판정하면 된다.

5) Language Entropy

따라서 lg.entropy 는 다음과 같이 계산이 가능하다.

• 구하고자 하는 것은 H(L) 이었지만 이를 model prob 과 결합한 H(p,m) 으로 근사하였다. (Cross entropy)
• 언어가 stationary, ergodic 하다고 할 때, 엔트로피는 하나의 긴 문장의 확률만으로 정의할 수 있었다 (Stationary ergodic process)

6) PPL derivation

이 값을 가지고 최종적으로 PPL derivtion 을 할 수 있다.

Lg. entropy 의 값을 H(W) 라 할 때, 식을 전개하면 다음과 같이 된다. model prob 을 표기만 p로 했다.

이전에 엔트로피는 컴퓨터는 2진수로 표기할 수 있는 정보의 크기라했다. 따라서 다음과 같이 2^H(W) 로 표시하고 전개하면

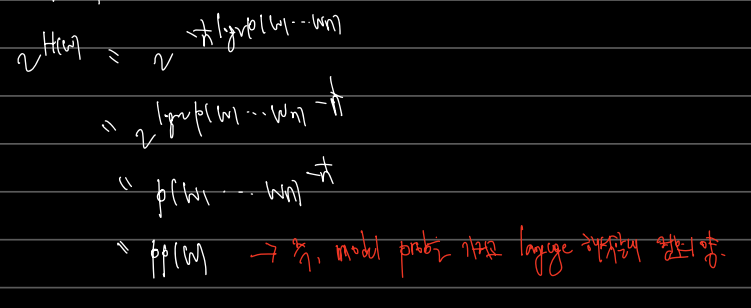
2^H(W) 의 실제 엔트로피를 p라는 model prob 을 가지고 해석할 때 정보의 양이다. 나타난 식은 perplexity 의 식과 같다!

조금 더 명확히 서술하면 train data 를 가지고 model probability 를 만들고, 이를 가지고 실제 세계의 language 를 해석함에 있어서 정보가 작으면 작을수록 잘 만들어진 model 이라 생각하는 것이다.