[NLP] Transformer

1. Transformer Architecture

✅ Limitations of RNN
문장은 순차적인 시퀀스, 시간의 흐름이 있으므로 이를 모델링할 수 있는 RNN 계열이 모델이 자연어처리에서 유용하게 작동했다. 그러나 RNN 계열의 문제는 공통적으로 다음과 같은 한계를 가졌다. (문제1)

• Vanishing gradient
  장기 종속성의 첫번째 파생 문제로, 오차가 멀리 전파될 때 계산량이 많아지고, 전파되는 길이가 길이가 길어질수록 기울기의 양이 점차 적어지는 문제점이 있었다.

• Exploding gradient
  큰 기울기가 계속 곱해지면서 기울기가 너무 커지는 문제가 발생한다.

왜? 전체 loss 는 각 time step 마다 loss 의 합이며, 해당 time step 의 loss 는 이전 hidden state 에 대한 미분을 연속적으로 포함한다. 즉, 이전 time step 의 hidden state 의 값 역시 계속해서 곱해지면서 값이 소실되거나 폭주한다.

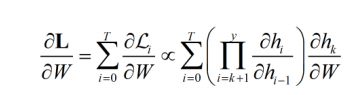
괄호친 부분의 값(time step i의 hidden state, i-1 의 hidden state)이 1보다 크냐, 작냐에 따라 작으면 소실, 크면 폭주할 것이다. (0.99^100은 0.37이다.)

어쨌든 이렇게 RNN 기반으로 계산하게 되면 배치 안에서의 병렬화는 가능하지만 time step 에서의 병렬화는 불가능하며 (문장을 한번에 계산해내는 것은 불가능하며) 따라서 이전 time step 의 계산이 끝나야지만 현재 time step 을 계산할 수 있다는 문제도 존재한다. (문제2)

✅ Overall Transformer Architecture
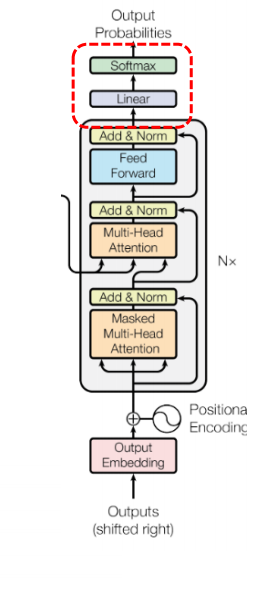
이러한 문제를 토대삼아 "Attention is All You Nedd" 라는 논문이 발표되었다. 전체적으로는 Encoder-Decoder 구조로 이루어져 있으며, Encoder 에서는 입력 토큰의 임베딩 벡터시퀀스, Decoder 는 인코더의 출력과 이전 디코더의 출력값을 이용해 한번에 한번씩 생성하는 일반적 구조이다.

공통적인 인코더, 디코더 구조를 가진 모델 2개를 보자.

• RNN + Attention
  
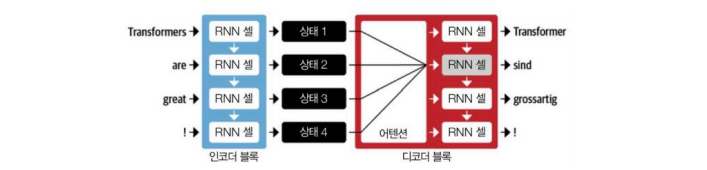
  디코더에서 하나씩 출력할 때 Attention 을 적용하여 인코더에서 어느 부분에 집중할지 결정하고, 디코더 이전 셀의 입력 + 인코더 집중된 셀 입력을 받아 계산한다.

• Transformer Encoder-Decoder
  
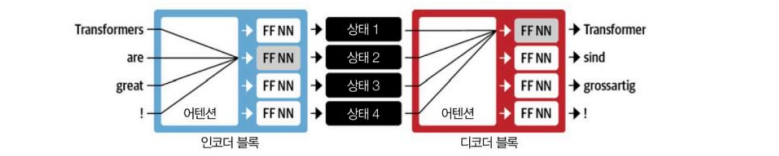
  트랜스포머 인코더-디코더의 경우 입력이 들어오면 한번에 어텐션을 구하고, 피드포워드 신경망을 한 번 통과시켜서 상태를 만들어낸다. 디코더는 각 만들어진 상태에서 어디에 집중해내는지를 계산하고, 역시나 피드포워드 신경망을 통과시켜 output 을 계산한다.

따라서 이전 단어를 계산하지 않아도 다음 단어를 계산하는 것이 가능해진다. (병렬화)

다음과 같은 그림으로 구체적으로 확인할 수 있다.

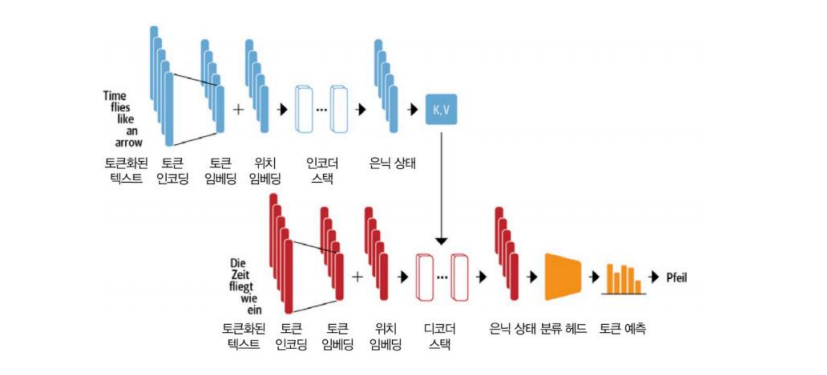
• 각 토큰의 임베딩에 위치 임베딩을 더한다
• 이 값을 인코더 스택에 통과시켜서 hidden state 를 만든다. (토큰마다)
• Key, Value 추출
• 디코더에서는 예측할 단어의 전 텍스트에 대해 임베딩 + 위치 임베딩을
• 디코더 스택에 통과시킨다
• 디코더 스택에서는 디코더의 이전 임베딩 + 인코더의 압축 정보 (Key, Value) 를 입력으로 받는다
• 디코더 스택에서 hidden state 를 만든다
• 예측을 수행한다.

2. Transformer Encoder

트랜스포머 인코더에서의 입력은, 입력 시퀀스를 토큰화한 것이며 출력은 인코딩된 표현이다.

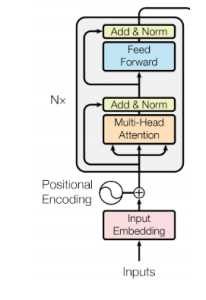
1. Position Encoding

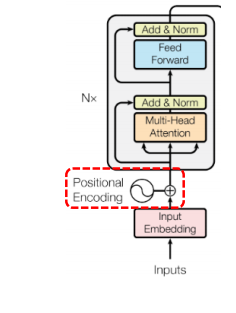
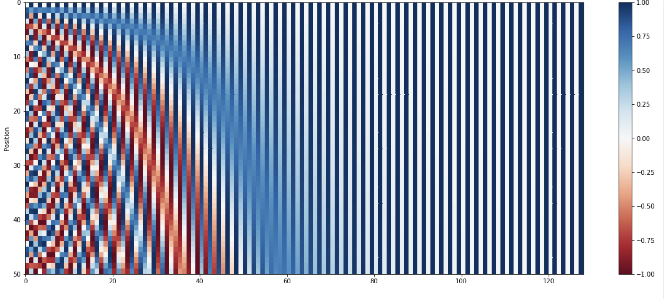
입력 토큰 벡터에 위치 패턴을 더해주는 것을 의미한다.

• 정현파
  

Position Encoding

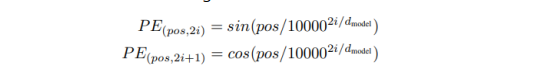
최근의 모델들은 Position Encoding 을 고정된 숫자로 주지않고 훈련가능한 값으로 준다. 따라서 원하는 Task 에 따라 어떤 위치에 집중할지 학습 가능하게 만들 수 있는 방법이 존재한다.

2. Multi-Head Self-Attention

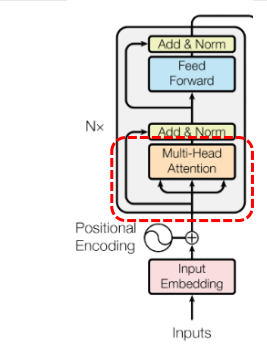
• input: input embedding Seq
• output: output embedding Seq (consider context by Self Attention)

기본 어텐션의 경우 토큰 임베딩 시퀀스을 입력으로 받고, 어텐션이 적용된 토큰 임베딩 시퀀스를 출력으로 한다. (x1', x2', x3', ... xn' 출력. 값을 낼 때 곱해지는 각 가중치의 합은 1 = 가중치는 확률과 같다고 이해하면 된다.)

Self-Attention 은 Attention 의 가중치가 인코더의 표현만 보고 계산한다는 의미이다. 이전에 Attention 은 현재 디코더의 time step 에서 예측할 때, 예측하려고 하는 단어와 유사도를 구하고.. 곱하는 과정을 거쳤지만 Self-Attention 의 경우 인코더만 보고 계산한다는 것이다.

트랜스포머의 경우 디코더에서도 Attention 을 계산하는데, 디코더에서도 Self-Attention (이 경우 디코더의 토큰끼리) 를 계산한다.

🤔 왜 Attention 이 아닌 Self-Attention 을 계산할까? 이를 통해 Context 가 적용된 임베딩을 만들 수 있기 때문이다. (문장 안에서 다의어, 동음이의어의 경우 문장의 다른 곳에서 힌트를 찾는다 생각하자.) 따라서 Self-Attention 의 인풋은 원래 가지고 있던 토큰들의 표현인데, Self-Attention 을 거치며 문장 안에서 Context 를 고려한 토큰들의 표현을 만들 수 있다. 또한 입력 시퀀스만 보고 임베딩을 결정하므로, time step 을 고려할 것 없이 한 문장을 그대로 받고 연산하고 한 문장(의 표현)을 출력하면 되므로 병렬 프로그래밍이 가능해진다.

🤔 Q, K, V Attention

• Query
  찾고 있는 요소로, 검색어에 해당한다. 이전의 decoder hidden state 와 같다. 현재 구하려고 하는 값.

• Key
  요소들의 이름표에 해당한다. 라벨, 식별자이다. 이전의 encoder hidden state 와 같다. (쿼리와 곱해 attention score 를 만들고, distribution 을 만든다)

• Value
  실제 요소의 정보나 컨텐츠이다. 키를 식별해낸 후 찾는 것을 뜻한다. 다시 곱해지는 encoder hidden state 와 같다.

순서) 쿼리와 키의 값을 곱해서 유사도 계산을 한 다음(attention score), scaling 을 통과시킨 후(Attention distribution) Value 를 곱해준다(attention output). 따라서 전체적으로는 내용 Value 와 attention distribution 을 곱하는 과정이다. distribution 은 Attention score 를 확률값으로 바꿔준 것으로, 쿼리와 키가 유사할 확률값이다.

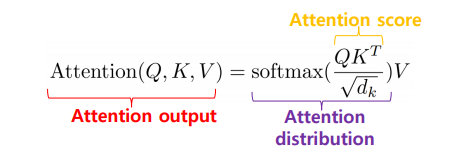
🤔 셀프 어텐션과 어떻게 Q, K, V 가 연결될 수 있을까..? 일단 지금까지 내가 알고 있는 Q, K, V 를 계산하려면 인코더의 attention output 을 계산할 때 디코더의 time step 값이 필요하다는 것인데. (인코더, 디코더에서 일어나는 Attention 계산에 활용??)

Scaled Dot-Product Attention

1. 인코더에 입력된 토큰 임베딩을 Q, K, V 벡터로 투영한다 (Self Attention 을 계산해야 하므로 Q, K, V가 다 Just 인코더의 hidden state 다 => 위의 질문이 해결되었다. 인코더의 atttention 을 계산할 때 디코더 필요없이, Q, K, V를 다 입력 시퀀스의 hidden state 로 통일하는 것이다. 얻고자 하는 것, 식별자, 내용 모두 입력 문장 안에서 해결)
2. Attention score 계산한다: Q X K^t
3. Attention Weight 계산: scaling, Softmax 를 취해서 합이 1이 되는 가중치로 게산.
4. 토큰 임베딩을 업데이트한다: 원래 가지고 있던 hidden state 값 (Value가 되겠다) 에 3에서 계산한 Attention Weight 를 곱해 임베딩을 업데이트한다.

그러나 동일한 Q, K, V 를 사용하면 자기 자신 단어에 대한 score 만 높아지므로 Multi-Head Attention 을 도입한다.

Multi-Head Attention
서로 다른 Q, K, V를 탄생시키자는 목표로, Linear Transformation 을 적용시키는 것을 말한다. Q, K, V 에 각각 Linear 연산을 적용시켜서 각각 다른 3개의 값을 만든다음 Scaled Dot-Product Attention 을 적용시킨다는 것이다. (어떤 값을 곱해?)

어차피 뭐가 됐든 비슷한 값 3개를 곱할건데, 조금씩 다른 값을 곱하자.. 그러면 어떻게 다른 값을 만들까? 하다가 문장의 다른 요소들에 집중하자! 생각한 것이다.
(마지막 곱하는 V가 최종적으로 중요할 것 같은데.. 뭘 곱할까? => 이 Linear 가중치 알아서 학습? 알 수 없음?)

Head (=Linear 가중치 matrix) 마다 뻥튀기 하는 값이 다 다르다. 어떤 Head 는 명사, 다른 Head 는 주어와 동사, 다른 Head 는 단어마다 의미적으로 유사한 정보 집중하도록 뻥튀기 할 수 있다.

정리하자면, 동일한 Q, K, V에 Linear 연산으로 뻥튀기하는데 (각각 다르게 뻥튀기) 이를 Multi-Head 연산이라하고, 계산된 3개의 값을 각각 이전과 같이 Scaled Dot-Product 해주는 과정을 거치면 된다.

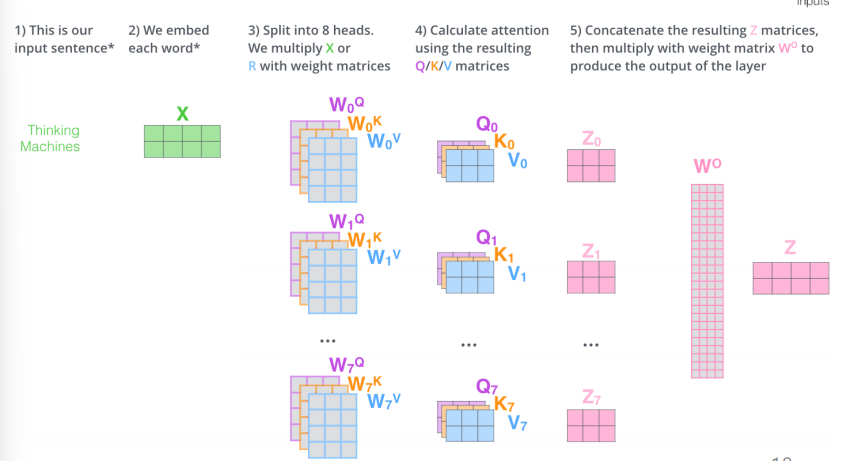
• 입력 x
• 8개의 Head 사용. 해당 Head 마다 다른 Q, K, V 를 만든다. (Linear 가중치 Matrix 를 Head라 생각하자.)
• 하나의 Head 에 각각 Q,K,V 하나씩 출력 => multi view 를 담은 Q,K,V 8개
• 8개의 z 계산. z는 Q,K,V 내부적인 순서를 그대로 따른다
• z들을 concat 하고, 가중치 W를 한번 더 곱한다. (크기를 맞추는 목적이라 생각하자.)

3. FFNN

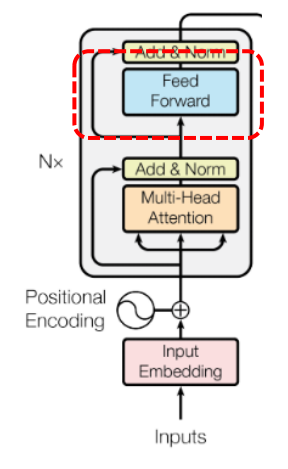
• Feed Forward 구조
  두번의 선형 변환으로 이루어져 있다. 첫번째 선형 변환과 두번째 사이에 activation function 을 한번 적용하게 된다. 이렇게 2번의 FFNN 를 적용함으로써 보다 복잡한 관계를 capture 하고, 비선형성을 추가할 수 있게된다.

4. Add & Norm

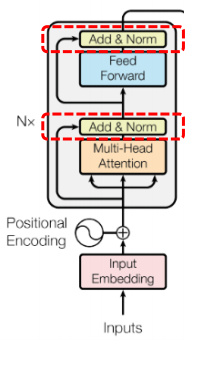
Add 는 Residual Connection 으로, f(x) = f(x) + x 로 함수를 적용시킨 결과에 기존 입력 결과를 더한 것을 출력으로 사용하겠다는 것이다. Residual Connection
Norm 은 평균이 0이고 분산이 1인 값으로 정규화하는 과정을 의미한다. 이렇게 Add & Norm 연결을 Multi-Head Attention 의 출력값과 Linear 연산 2번 후의 출력값에 적용함으로써 Gradient 를 안정적으로 만들고 과적합을 방지할 수 있게된다.

3. Transformer Decoder

디코더의 경우 입력은 토큰화된 입력 시퀀스이고, 예측된 토큰을 결과로 반환한다. 기존 인코더와의 차이점으로는 두 개의 어텐션을 사용한다는 점을 들 수 있다. (Masked multi-head attention, encoder-decoder attention)

1. Masked Multi-Head Attention

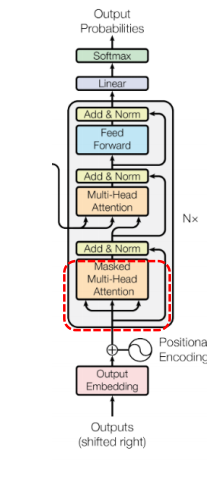
디코더의 경우, 디코더의 토큰들이 서로에게 어떻게 영향을 주는지 가중치를 계산한다. 이경우에도 역시나, Q, K, V가 디코더의 입력 시퀀스로 동일하다.

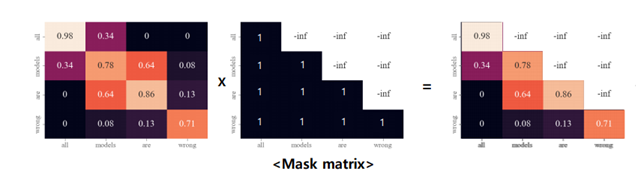
그러나 디코더에서 Self-Attention 을 계산하기 위해선 입력 시퀀스를 전부 다 보아야 하는데, teacher forcing 으로 학습하는데 있어서 미래의 값을 알고 학습하는 것은 cheating 이다. 따라서 Mask matrix 를 통해 미래 시점의 토큰에 attention 되는 것을 방지한다. (뒤 단어에 대해선 Self-Attention 연산에 포함시키지 않는다.) 이를 Masked Attention이라고 하며, 아래의 그림과 같이 미래의 값에 -inf 값을 곱해주는 것이다. Mask 계산은 언제 적용하느냐? attention score 계산 후에 적용한다. 가장 왼쪽의 값이 attention score, 두번째 값이 곱해지는 Mask matrix, 결과값이 mask 된 결과이다.

2. Multi-Head Attention(=Encoder-Decoder Attention)

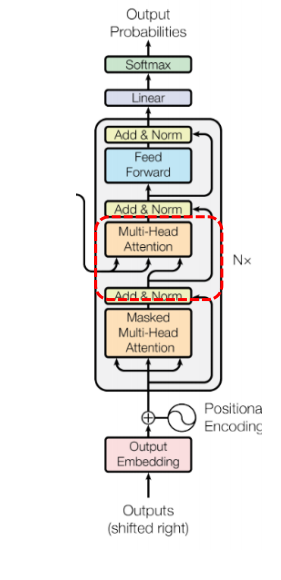
이번의 어텐션 계산은 디코딩 시에 인코더의 어떤 부분에 영향을 받는지 가중치를 게산하게 된다. Q의 경우, 이전 디코더의 출력값이며, K,V 는 인코더의 마지막 layer 에서 출력값이다.

전체 입력 시퀀스를 다시 보고, 무엇이 중요한지 계산하며, 출력을 해내는 부분이다.

3. Linear, Softmax
최종 결과값을 만들어내는 부분이다. 이전에 봤던 Linear, Softmax 를 적용한다. Linear 의 주요 목적으로는 예측 값으로 size 를 맞춰주는 것이며,(반환되는 값은 logit이다.) Softmax 는 역시나 확률값으로 변경함을 뜻한다. 디코더에서 Softmax 를 거친 최종 결과값이란 다음 예측 단어가 될 것이다.