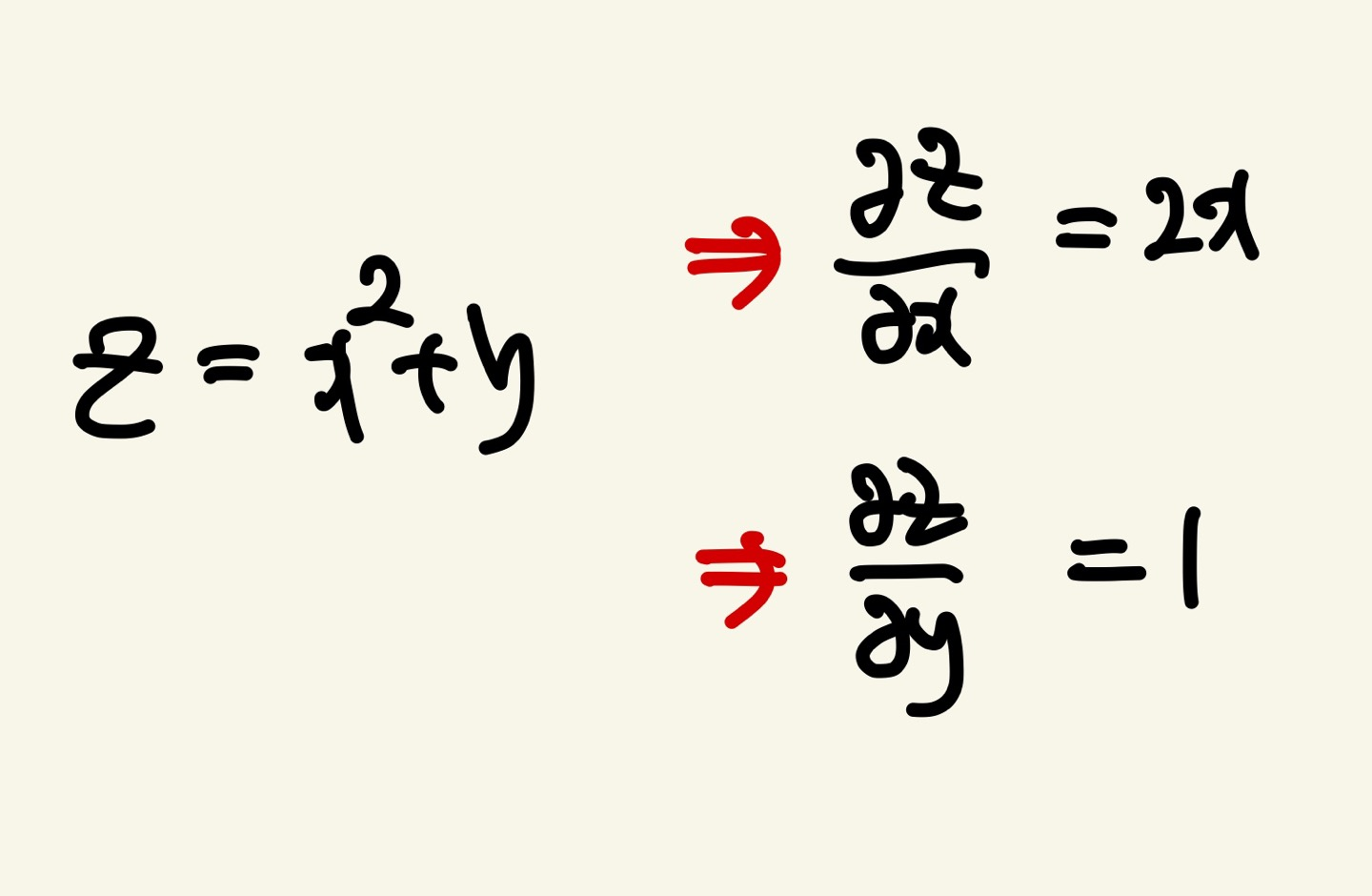BackPropagation(오차역전파)에 앞서
BackPropagation(오차역전파)에 대해 알기전에...
오차역전파는 머신러닝/딥러닝에서 매우 중요한 알고리즘입니다. 따라서 오차역전파를 설명하기 전 알아야 할 내용을 말씀드리겠습니다.
partial derivative(편미분)
편미분을 사전적으로 정의하면 다변수 함수에 대하여 그 중 하나의 변수에 주목하고 나머지 변수의 값을 고정시켜 놓고 그 변수로 미분하는 일 입니다.
예시를 보여드리겠습니다.
먼저 y는 종속 변수, x는 독립 변수입니다. 위 식은 y에 대한 x의 미분 식이고, x(독립변수)값이 변할때 y(종속변수)가 변하므로 y의 값이 x에 따라 어떻게 나타내는지 보여주는 도함수 입니다.
미분을 한 값의 2는 x의 값이 1 증가하게 되면 y값은 2가 증가한다는 의미가 됩니다.
하지만 위 식은 단순히 1변수함수입니다.
다변수 함수는 종속변수가 1개, 독립변수가 2개인 함수를 뜻합니다.
예시를 보여드리겠습니다.
z는 종속변수, x와 y는 독립변수 입니다. 편미분 "∂"로 표기합니다.
각 x에 대한 미분과 y에 대한 미분은 기울기를 의미하고 변화량을 뜻합니다.
아래 그림은 Gradient Descent의 공식입니다. 여기서 이 편미분은 손실함수에 대한 가중치를 미분할때 사용됩니다. 각 가중치들의 변화량을 알아야하기 때문에 편미분을 사용한다고 알아두시면 됩니다.
덧붙히자면, 신경망에서 Input Features들은 Constant라고 말씀드렸습니다. 그러나 weight들은 Parameter입니다. 계속 말씀드리지만 예측값과 실제값의 차이를 줄이는 것이 신경망의 목표입니다. 이 신경망에서 저희가 조절할것은 weight들 뿐 입니다. 그렇기 때문에 가중치에 대한 편미분값을 구하여 변화량을 알아내면 어떤 가중치를 조절해야 실제값에 가까워지는지 알 수 있게됩니다.
Chain Rule(연쇄법칙)
Chain Rule은 변수가 여러 개일때 어떤 변수에 대한 다른 변수의 변화율을 알아내기 위해 사용됩니다. 말이 좀 어려울 수 있습니다. 그림으로 보시겠습니다.
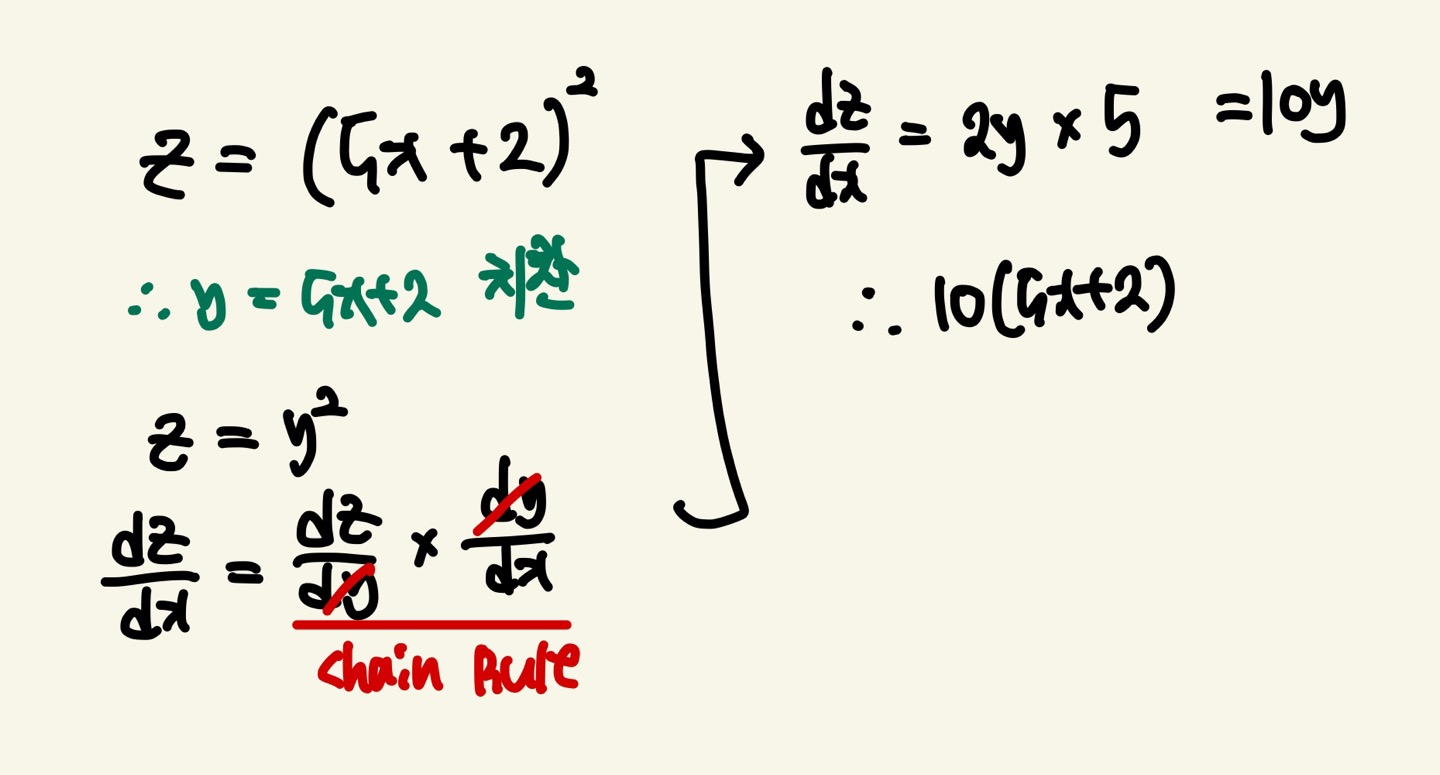
Chain Rule은 합성함수의 미분에서 사용됩니다.
z는 x에 대한 식으로 나타나져 있었지만 y = 5x+2로 치환하게 되면서 z는 y에 대한 식으로 바뀌었습니다. 하지만 본질은 같습니다. y로 치환이 되어도 z는 x에대한 식인 것은 변함이 없습니다. 따라서 이 함수는 함성함수이고 x에 대해서 미분하기 위해서는 다음과 같은 Chain Rule을 이용해 dz/dx를 구하게 됩니다. dz/dy * dy/dx가 dy로 약분된다고 생각하시면 편합니다. (엄밀히 말하면 약분이 아닙니다.각각 독립적인 값을 갖는 것 입니다.)
이러한 과정은 저희가 고등학교때 배운 함성함수의 미분입니다.
BackPropagation(오차역전파)
앞선 내용을 이해했다면, 오차역전파는 절대 어렵지 않습니다.
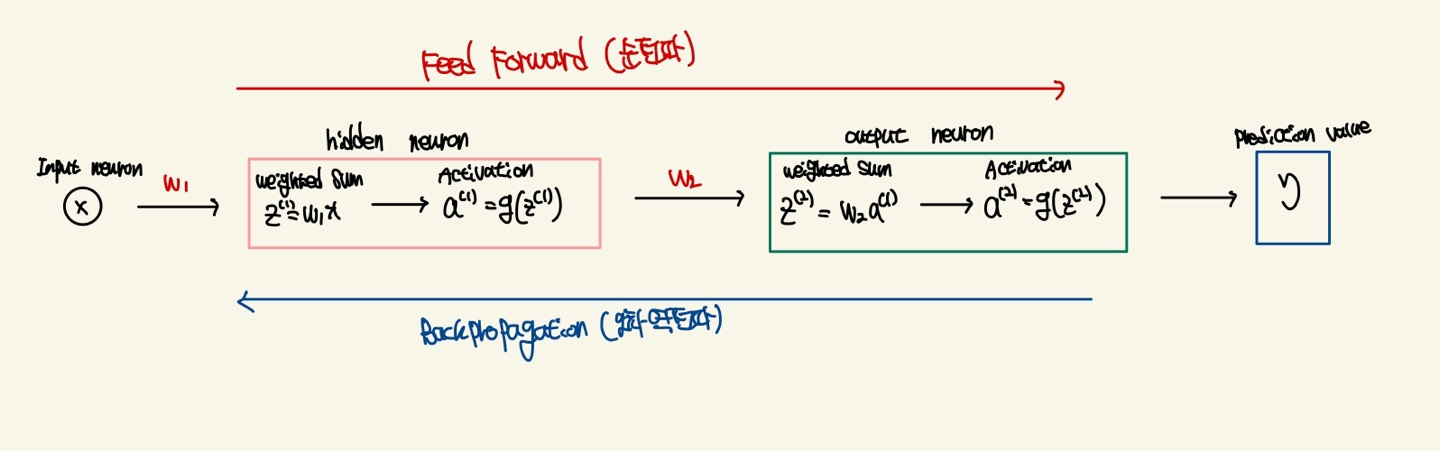
위 그림은 간단한 신경망을 나타냈습니다. 순전파를 통해서 예측값을 알아내고 오차역전파를 통해서 예측값과 실제값의 오차를 줄이기 위해 weight를 갱신해나갑니다.
오차 역전파는 Chain Rule과 편미분을 이용합니다. 그러면 가중치를 갱신하는 과정을 보여드리겠습니다.
W(2)를 구하는 방법은 다음과 같습니다.
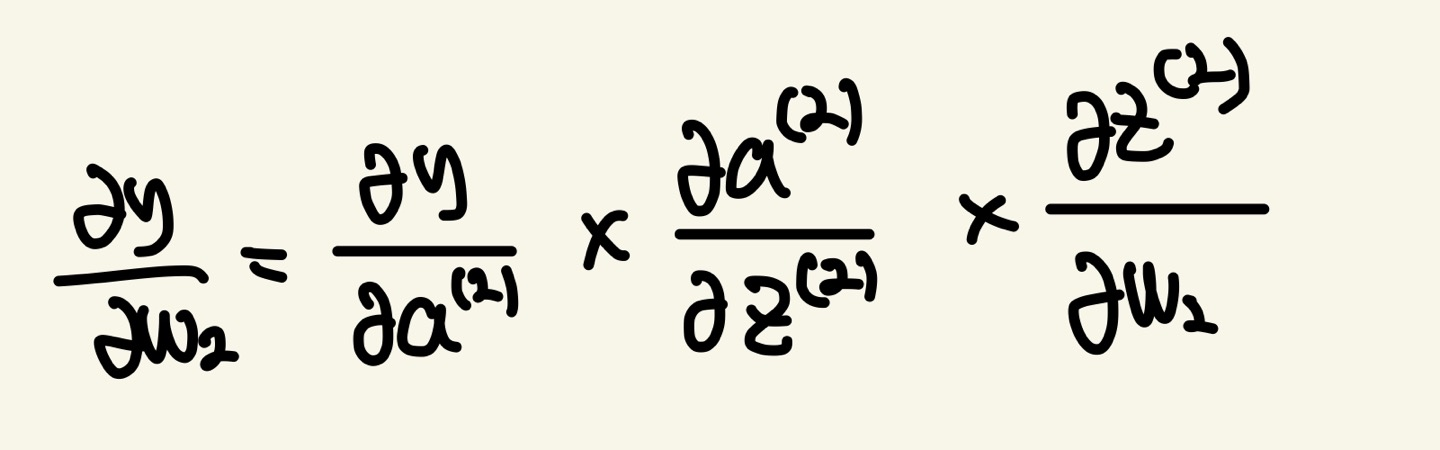
보시다시피 Chain Rule과 편미분을 이용하게 되면 ∂y/∂w(2)를 구할수 있게 된다는 것을 알 수 있습니다.
위 식을 분석해보겠습니다.
prediction value인 y는 output neuron에서 activation을 적용한 a(2)라는 값이 입력으로 들어옵니다. 이 값이 저 인공신경망에서는 예측값이겠죠?
그러면 y = a(2)라는것을 알 수 있습니다. 그러나 a(2)는 output neuron의 weighted sum의 값을 통해서 온 값입니다. 그러면 a(2)는 weighted sum의 변수를 포함하니, 이것은 합성함수의 꼴이 되는것을 알 수 있습니다. z(2)도 마찬가지로 w2에 대한 변수를 포함하니 이것또한 함성함수의 꼴이 됩니다.
그러므로 chain rule를 통해 ∂y/∂w(2)값을 구할 수 있게됩니다.
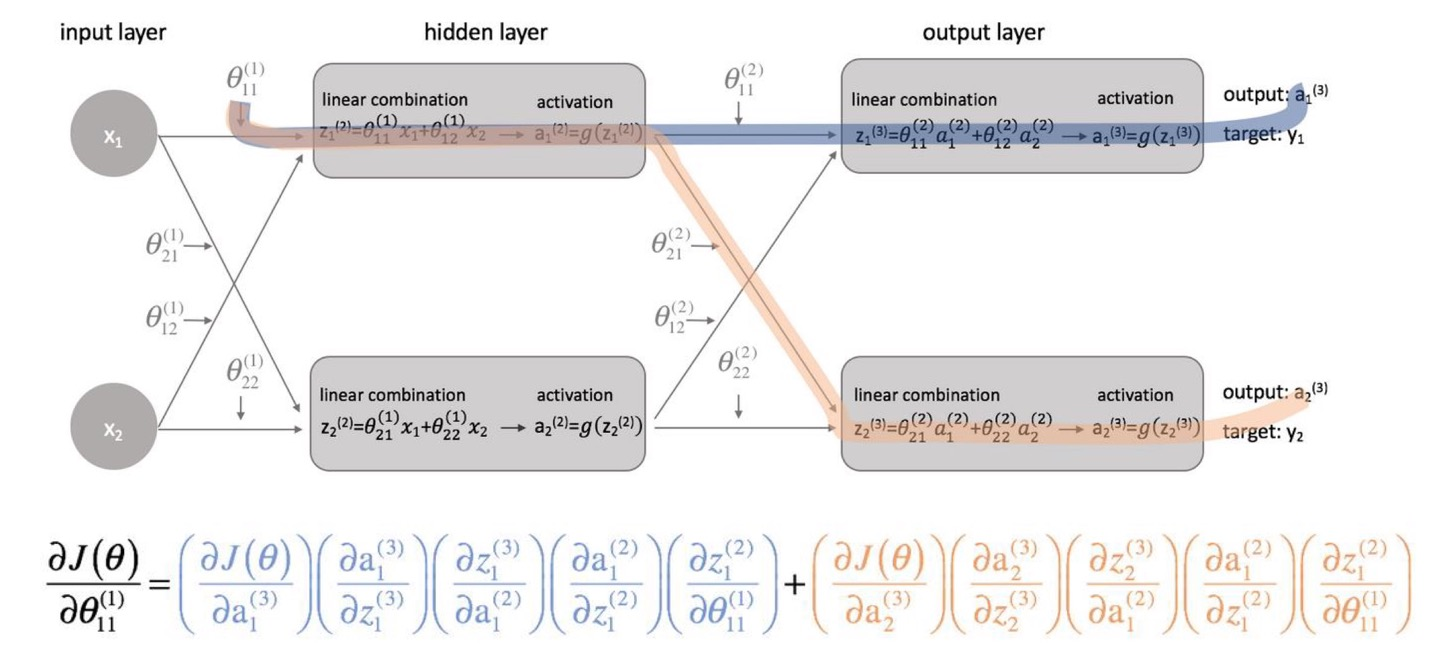
신경망을 더욱 더 구체화 시켜보았습니다.
Ouput Layer가 2개 이상일때는 θ11(1)을 구할때는 파란색과 살색이 영향을 미치는것을 알 수 있습니다. 각 layer가 복잡하고 뉴런이 많아질수록 backpropagation의 연산과정이 많아지고 복잡해지는것을 알 수 있습니다.
그리고 서로 다른 Path의 backpropagation은 값을 더하는것도 알 수 있습니다.