경사하강법을 더 알아보자
Gradinet Descent방식은 전체 학습 데이터를 기반으로 GD를 계산합니다. 그러나 입력 데이터 개수가 많고, Layer가 많을 수록 GD를 계산하는 많은 Computing 자원이 소모됩니다. 만약 전체 데이터에 관해 GD를 계산하게 된다면 메모리 부족으로 연산이 불가능 할 수 있습니다.
| GD(Gradient Descnet) | SGD(Stochastic Gradient) | Mini - Batch GD(Gradient) |
|---|---|---|
| 전체 학습 데이터를 기반으로 GD 계산 | 전체 학습 데이터 중 한 건만 임의로 선택하여 GD계산 | 전체 학습 데이터 중 특정 크기만큼(Batch 크기) 임의로 선택해서 GD 계산 |
-
SGD는 1건만을 선택하여 GD를 계산하는 방식입니다. 1건만을 선택해서 가중치를 갱신하다니, 실제값과 예측값의 오차를 줄일수있을까? 라는 생각도 드실수도 있지만, 의외로 정확도가 높습니다. 하지만 SGD는 훈련 데이터의 개별 샘플에 노출되어 가중치 갱신이 불안정할 수 있고, 수렴 속도가 느리며 노이즈에 민감할 수 있습니다.
또한 epoch마다 임의로 선택하는 데이터는 달라집니다. -
Mini - Batch GD는 만약 입력 데이터의 특정 크기만큼 임의로 선택해서 GD를 계산하지만, 이러한 방법은 잘 쓰이지 않습니다.
그러나, 전체 학습 데이터의 순차적인 Mini-Batch는 다릅니다. 전체 학습 데이터가 400건이 들어왔다고 가정하고, 임의로 분할한 개수(Batch_size)가 100이라고 가정해봅시다. 그러면 1번의 epoch를 도는데 400건의 데이터를 100개로 분할하여 총 4번을 나누어서 GD를 계산하게 됩니다. 그러므로 전체 학습데이터를 일정한 단위만큼 나누어서 GD를 계산하니 정확도가 높습니다.
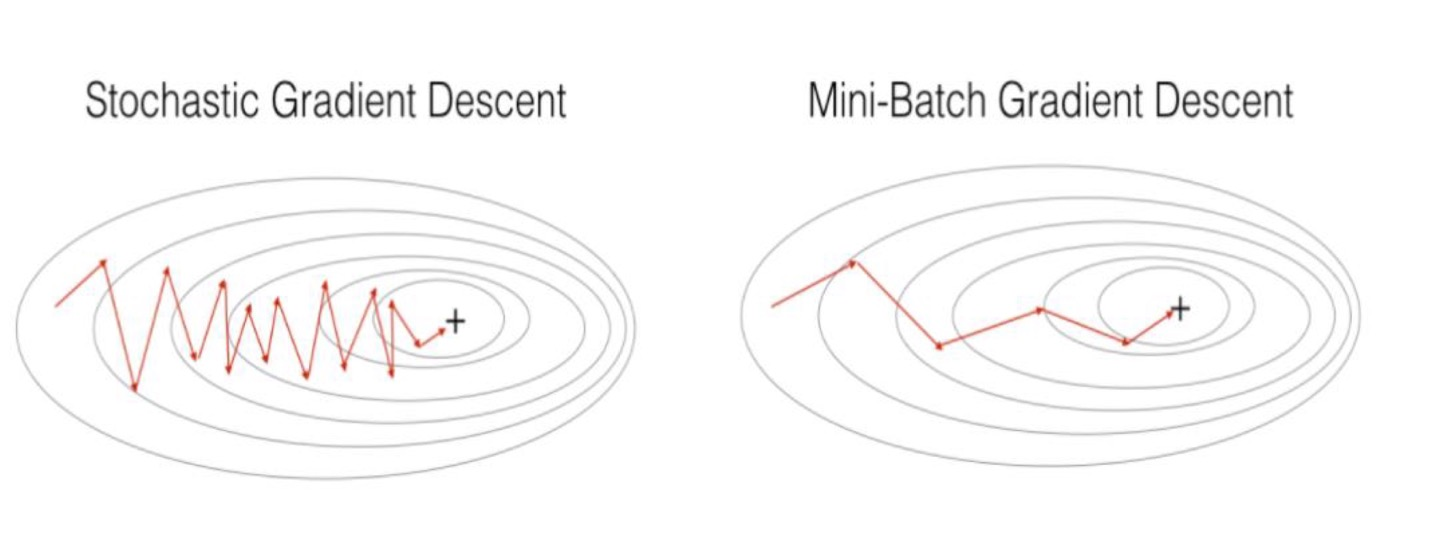
아래의 사진은 LOSS함수에서 수렴하는 과정을 담아낸것입니다. 확실히 SGD가 MINI BATCH보다 학습 속도가 느리고, 노이즈가 있고 불안정하다는것을 볼 수 있습니다.
epoch : 모델이 주어진 학습 데이터셋을 전체적으로 한 번 훑는 것을 의미합니다.
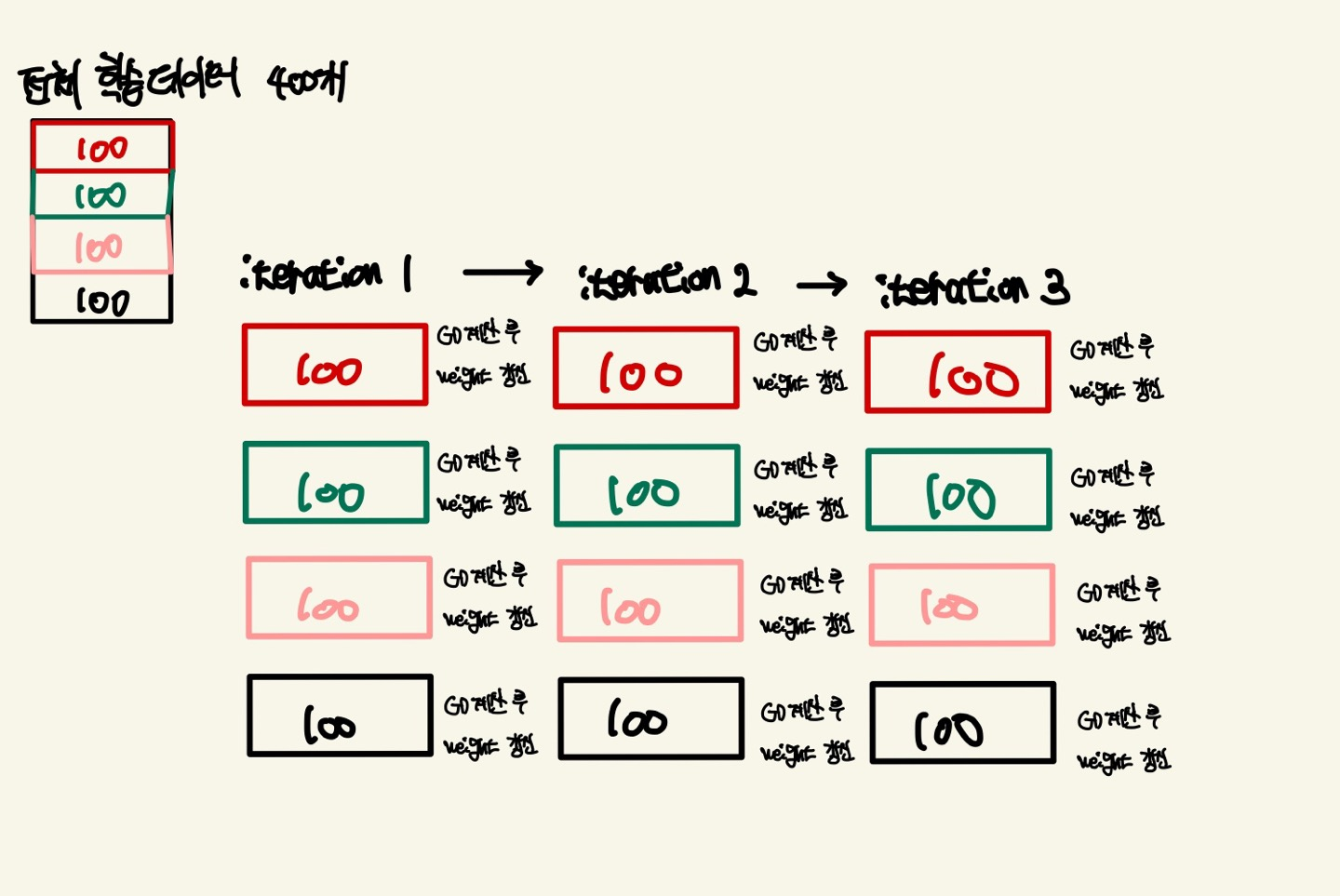전체 학습데이터의 GD를 계산하고 이를 batch만큼 분할하여 계산하니 메모리 효율성이 올라갑니다.그래서 일반적으로 이러한 Mini-Batch GD가 대부분의 딥러닝 Framework에서 채택이 되어 있습니다.
심층 신경망(다중 퍼셉트론) 이해
심층신경망은 다중 퍼셉트론으로도 불립니다. 퍼셉트론은 선형 문제만 해결할 수 있고 비선형 문제를 해결하지 못하는 단점이 있습니다. 그래서 기존의 퍼셉트론에서 Hidden Layer(은닉층)을 추가하여 비선형 문제를 풀 수 있게끔 신경망을 만들었습니다.
단순한 예시를 보여드리겠습니다.
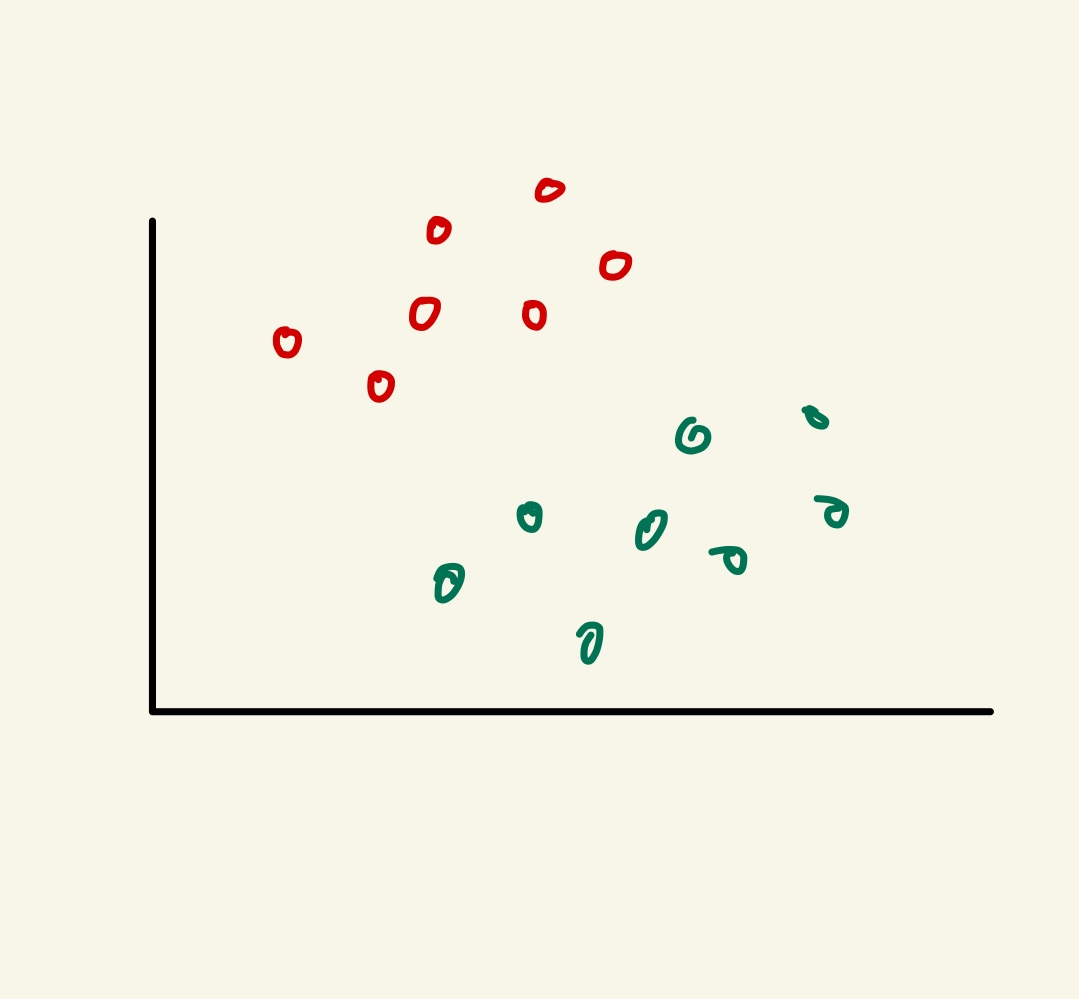
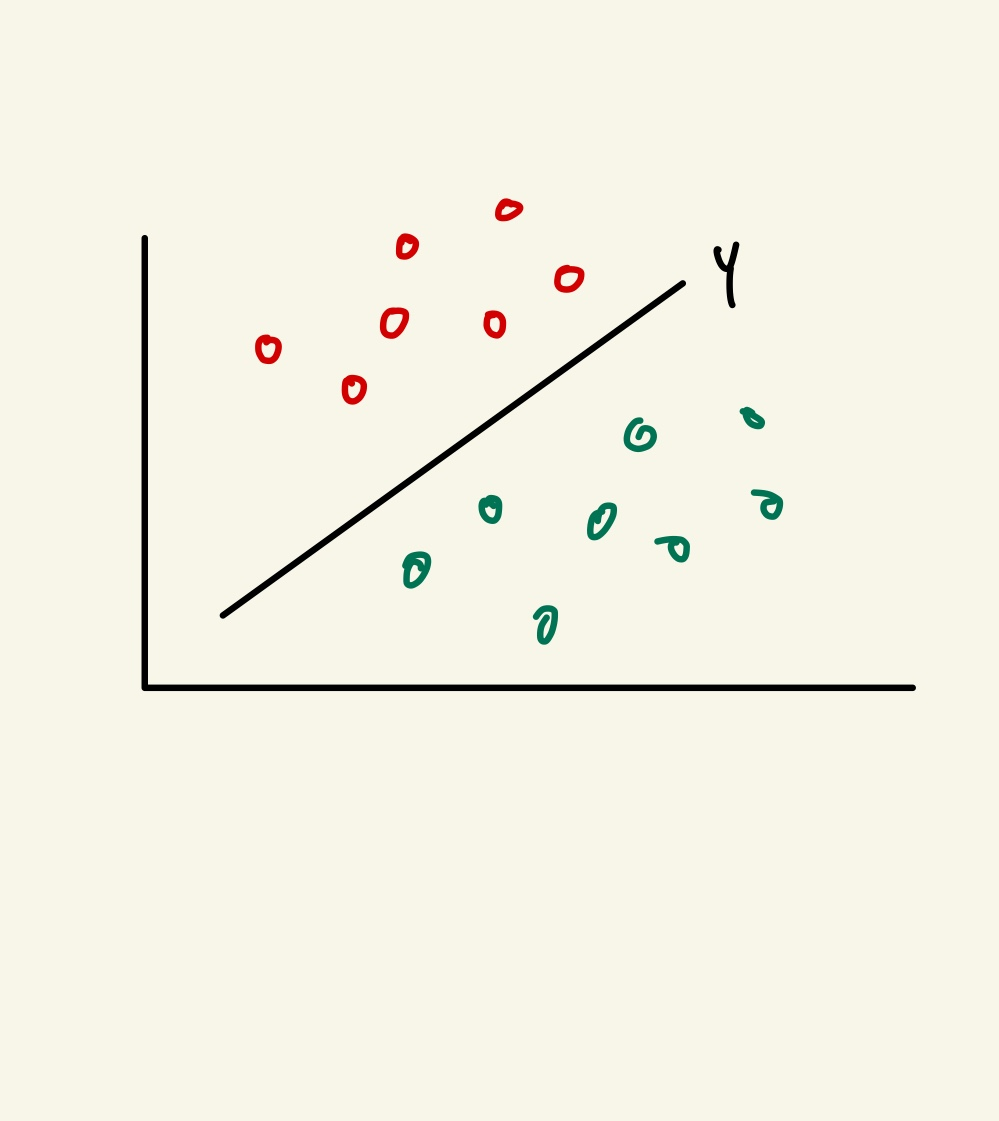
위와 같은 그림을 빨간색 점과 초록색 점을 어느 한 경계로 분류를 하고 싶다면
Y(선형 함수)를 그래프상에 나타내면 색상에 맞게 구별을 할 수 있겠죠? 이러한 방법은 퍼셉트론으로도 잘 판단 할 수 있었습니다. 그러나 점들이 섞여 있다면 말이 다릅니다. 단순히 선형함수로는 구별을 하지 못할 것 이라는것을 짐작 할 수 있습니다.
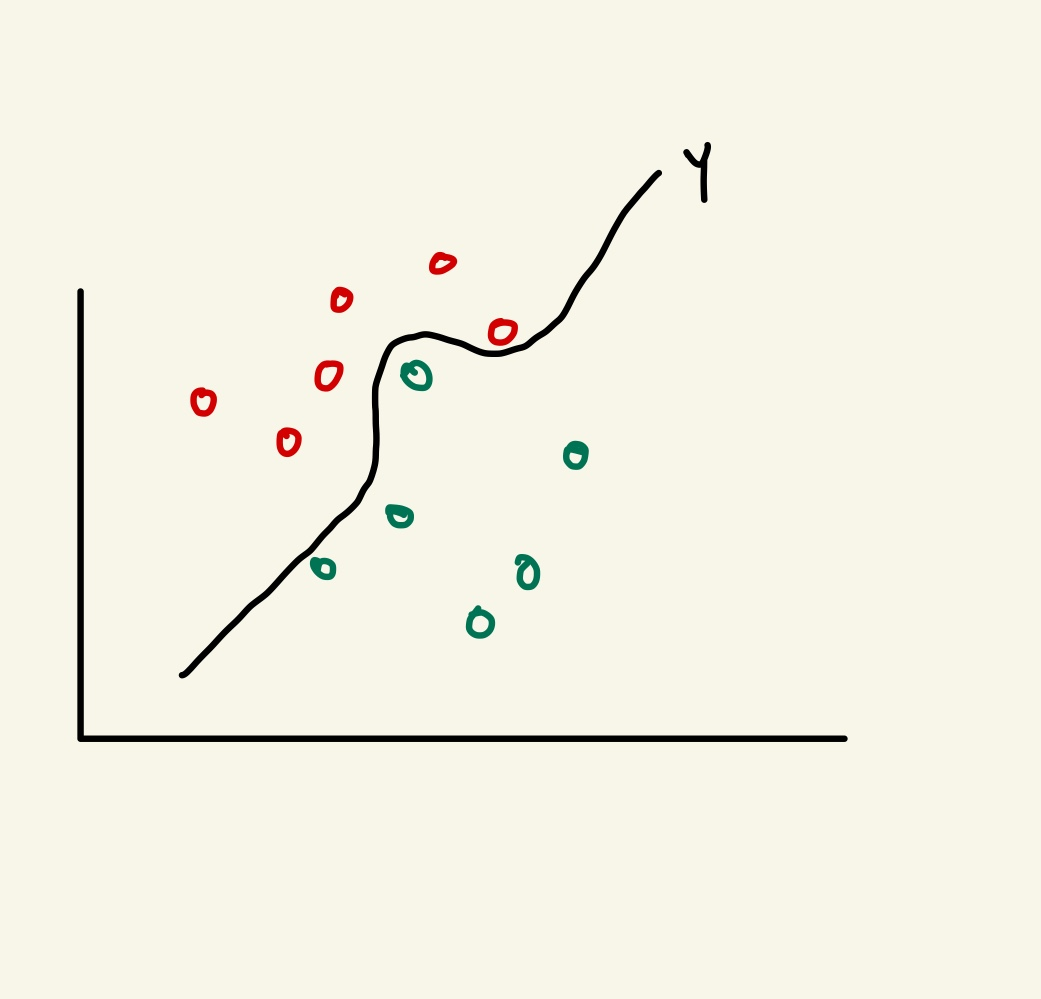
Y(비선형 함수)로 그래프 상에 나타낸다면 색상을 구별 할 수 있게됩니다.
따라서 저희는 비선형 함수로 보다 복잡한 문제의 해결을 위해서 은닉층(Hidden Layer)가 포함된 다중 퍼셉트론으로 심층 신경망을 구성합니다.
심층 신경망의 구조는 다음과 같습니다.
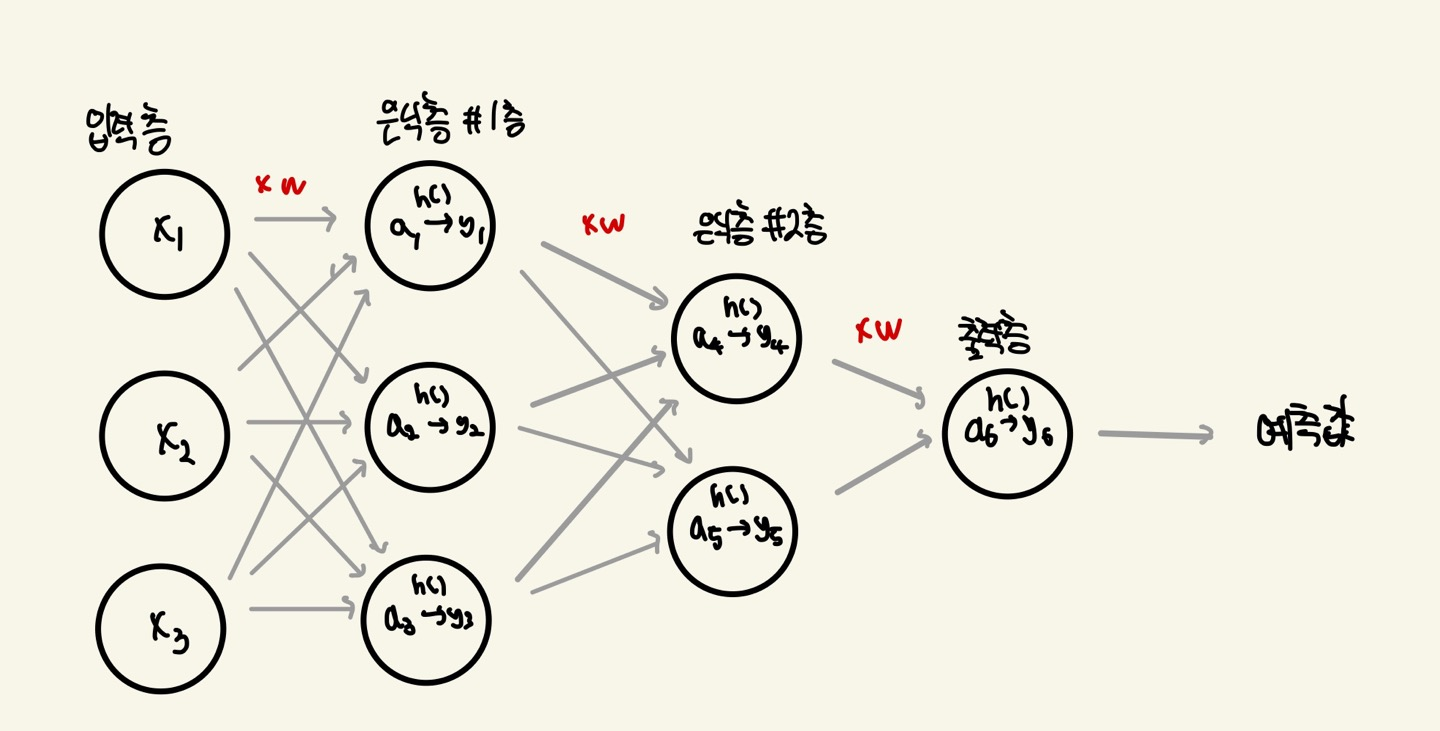
은닉층은 필요에 따라 더 추가할 수 있습니다. 각 은닉층의 노드(Node)들은 Weighted Sum값을 입력값으로 받습니다.
a : Weighted Sum
h( ) : Activation Function
y : output of layer
은닉층은 Weighted Sum값을 Activation Function으로 값을 가공합니다. 가공된 값은 다음 Layer의 입력값으로 사용이 되겠죠?
이러한 과정을 통해 예측값이 나오게 될것입니다. 이것을 Feed Forward 라고 부릅니다.
Feed Forward는 예측값을 나오는 과정이라고 생각하시면 됩니다.
활성화 함수(Activation function)은 인공 신경망에서 각 뉴런의 출력을 결정하는 함수입니다. 활성화 함수는 선형 함수를 비선형 함수로 변환하여 신경망이 복잡한 비선형 문제를 학습할 수 있도록 도와줍니다.
Feed Forward를 통해 예측값이 나오게 됩니다.
하지만 예측값과 실제값의 오차를 줄여주는것이 저희의 관건이라고 계속 말씀드렸습니다.
그 오차를 줄여주는것이 바로 Weight(가중치) 입니다. 이러한 가중치를 갱신하는 것은 GD(Gradient Descent)라고 말씀드렸죠?
GD를 계산하기 위해서는 편미분과정이 필요하다고 말씀드렸습니다. 퍼셉트론에서는 GD를 단지 편미분만 하면 가중치를 갱신할 수 있었지만, 다중 퍼셉트론은 Chain Rule을 이용한 편미분 값을 구합니다.
이러한 과정을 Back Propagation이라고 합니다. Back Propagation은 오차 역전파 라고 불리우며 다중 퍼셉트론의 편미분 값을 구하고 가중치를 갱신할수있도록 도와줍니다.
다음 포스팅은 back Propagation에 대해서 자세히 말씀드리겠습니다.
