본 내용을 이해하기위해 짚고 넘어가야할 내용을 말씀드리겠습니다.
회귀(Regression)
회귀는 여러개의 독립변수와 한 개의 종속변수간의 상관관계를 모델링하는 기법 입니다.
예를 들면 아파트의 방 개수, 크기, 주변 교통편 등의 독립변수에 따라서 아파트 가격인 종속변수가 어떠한 관계를 가지는지를 모델링하고 예측합니다.
이를 선형 회귀식으로 표현하면 Y = W1X1 + W2X2+..,Wn*Xn이라고 하면 Y는 종속변수, X는 독립변수가 됩니다. 이때 W는 독립변수(X)에 영향을 미치는 회귀계수 입니다.이 선형회귀식을 보면 우항은 Weighted Sum이고 좌항은 예측값이 되는것을 눈치 채셨을겁니다. 따라서 가중치는 선형회귀식의 회귀계수가 됩니다.
단순 선형 회귀(Simple Regression)
단순선형회귀는 독립변수가 1개가 있는 식입니다.
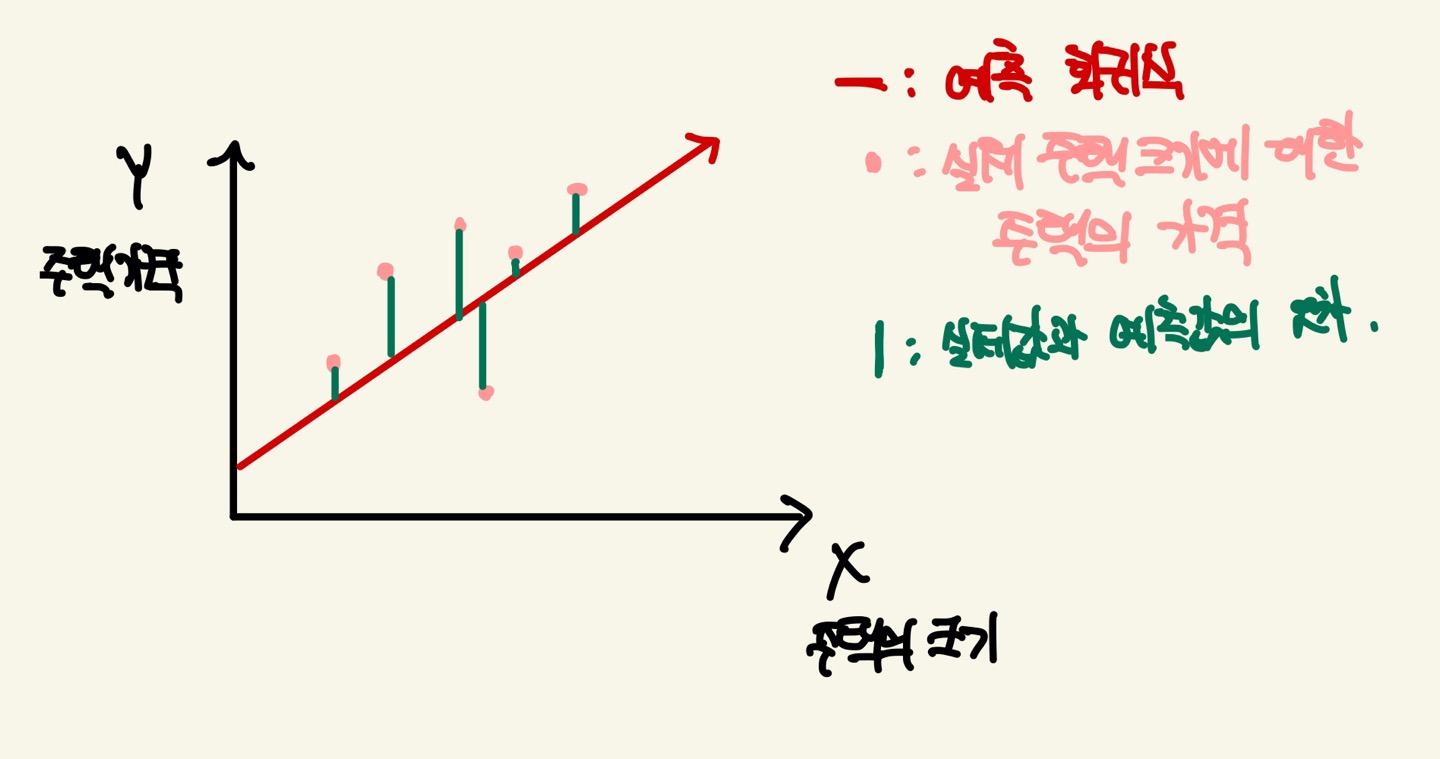
주택 가격(Y)는 주택의 크기(X)로만 결정 되는 단순 선형 회귀로 가정해보겠습니다.
이를 그래프로 나타내면 다음과 같습니다.
예측 회귀식은 Weighted Sum입니다.
Weighted Sum의 식은 W*X + B가 됩니다. 단순 선형 회귀안에서 최대한의 오류값을 줄이기 위해서 weight와 bias를 최적의 값으로 조절하면 오류값이 작아지는것을 알수있게 됩니다.
손실함수 개요
손실함수는 예측 값과 실제 값의 오차를 구하기 위한 함수입니다. 이 오차값을 통해서 모델을 평가하고 모델의 성능을 향상시키기 위한 방향을 결정합니다.
예측을 잘못하면 손실함수의 값이 높아지고, 예측이 정확할수록 손실함수의 값이 작아집니다. 즉, 예측값이 실제값에 근접하게 되면 손실함수의 값이 작아진다고 볼 수 있습니다.
손실함수는 경사하강법(Gradient Descent)를 통해 weight를 미분하여 손실함수의 값이 작아지도록 학습하게 됩니다. 손실함수와 경사하강법은 밀접한 관계가 있다는것을 알아둬야합니다
손실함수 종류
RSS(Residual Sum of Square)와 MSE(Mean Squared Error)
RSS는 오류 값의 제곱을 구해서 더하는 방식입니다. 일반적으로 미분 등의 계산을 편리하게 하기 위해서 RSS방식으로 오류 합을 구합니다. 단순 선형 회귀의 사진을 RSS로 나타내면 다음과 같습니다. X1,X2~Xn은 주택의 크기를 의미합니다.
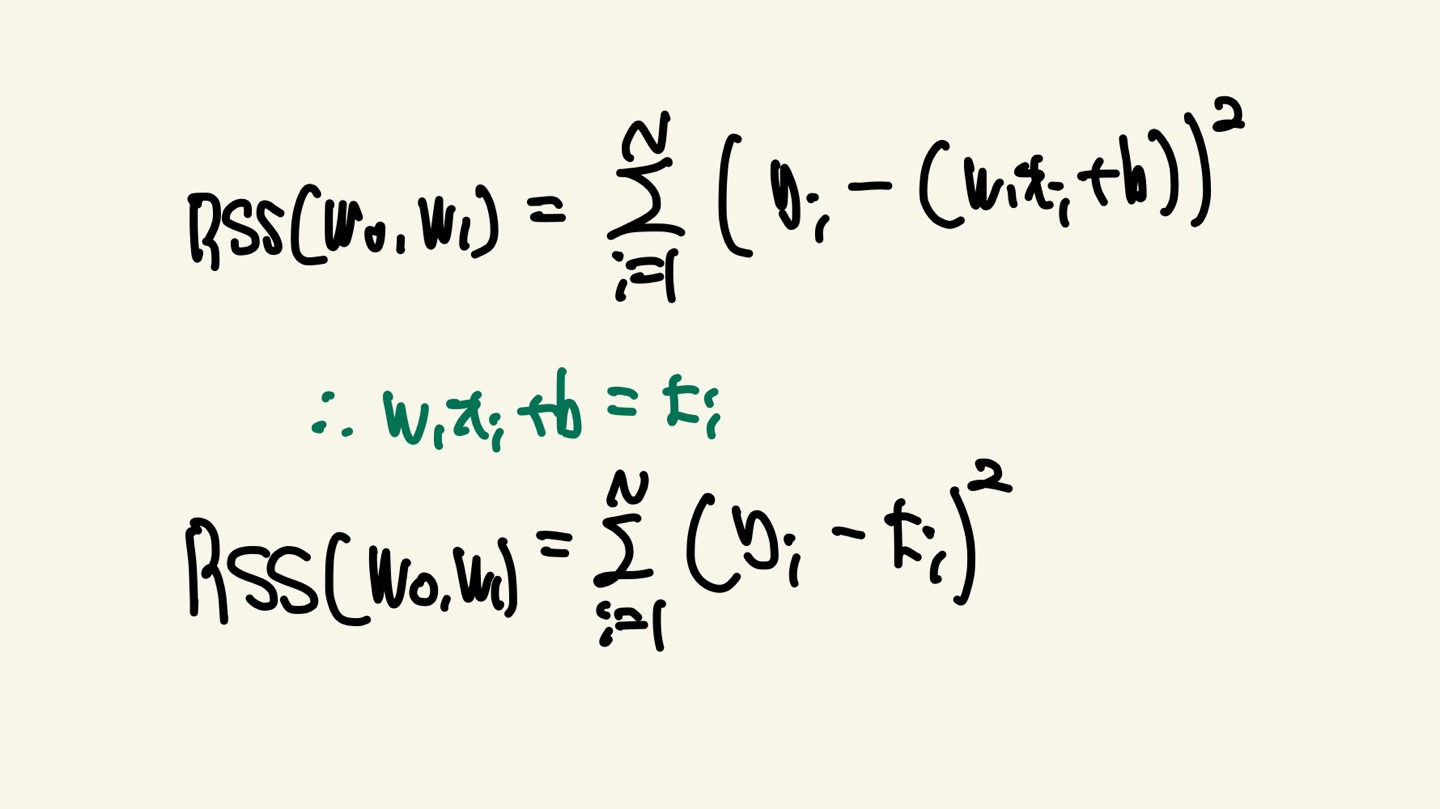
RSS는 회귀식의 독립변수 X, 종속변수 Y가 중심 변수가 아니라 W(회귀 계수)가 중심 변수임을 인지해야합니다. 따라서 X,Y는 Constant이고 W는 Parameter입니다. 이 개념은 Gradient Descent를 할때 매우 중요합니다.
RSS를 학습 데이터(Input Features)의 건수로 나누어서 MSE(Mean Squared Error)로 표현 가능합니다.
MSE는 평균적인 오차 크기를 제공하기 때문에 예측 모델의 성능을 직관적으로 이해할 수 있습니다
다음 사진의 N은 학습 데이터의 개수입니다.
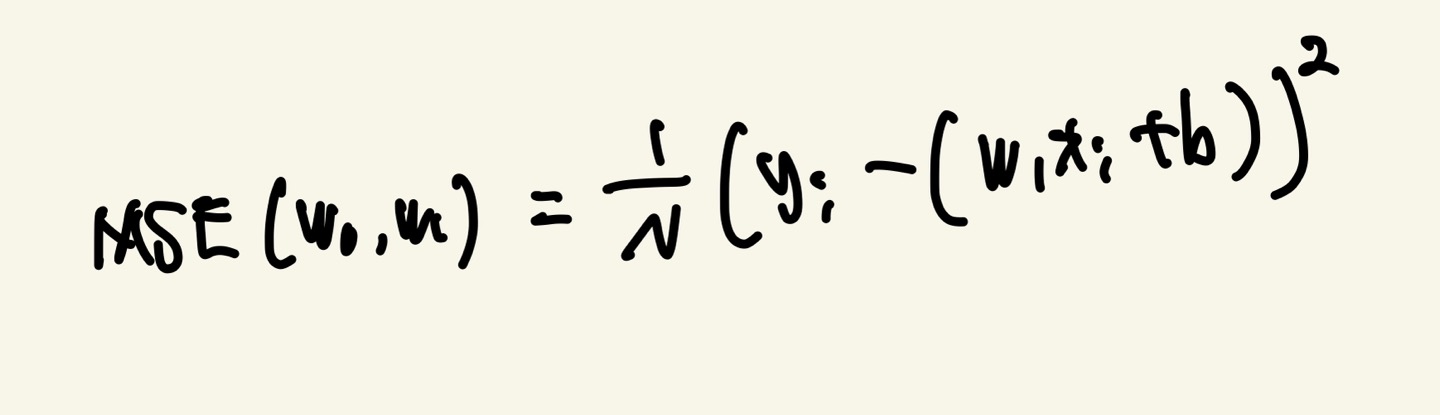
CE(Cross Entropy)
CE는 실제 클래스 값에 해당하는 활성화 함수 SoftMax의 결과 값에만 Loss값을 부여합니다.
아주 잘못된 예측 결과 값에는 매우 높은 Loss값을 부여합니다.
CE는 활성화 함수 SoftMax와 연관이 많으니 여기서는 단순히 있다는것만 알고 넘어가시면 될 거 같습니다.
Y(i)는 실제 값이고 Y(i)의 헷은 예측 값입니다.
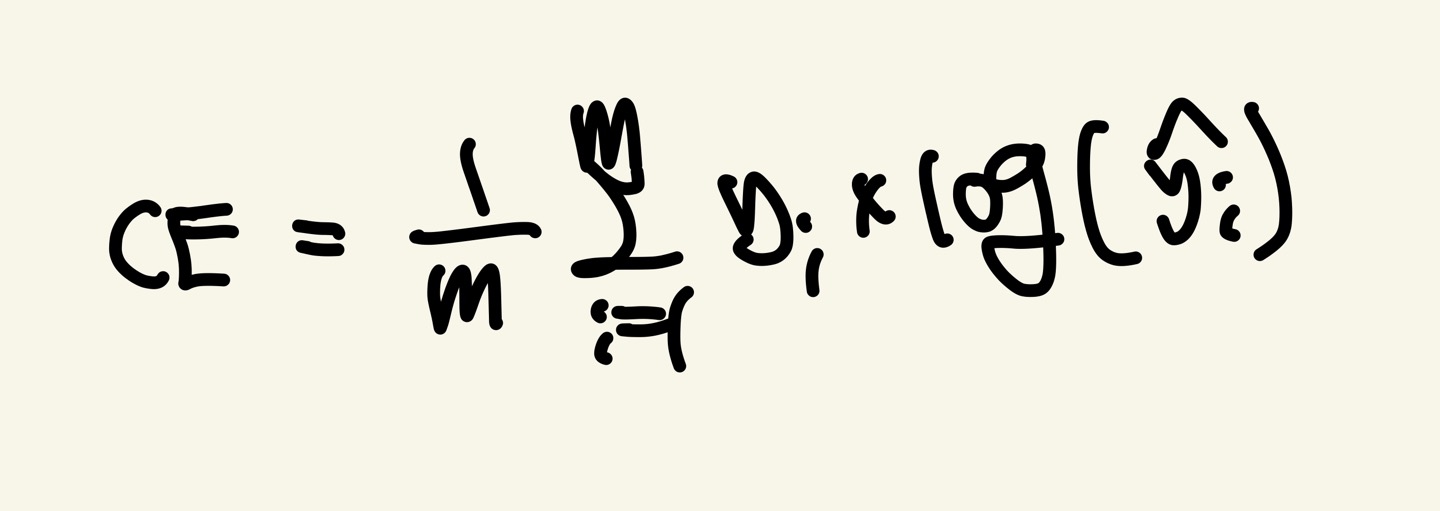
경사하강법 개요
경사하강법은 반복적으로 비용 함수의 반환값, 즉 반환값은 예측값과 실제 값의 차이가 작아지는 방향성을 가지고 weight를 지속해서 보정해 나갑니다.
만약 오류 값이 더 이상 작아지지 않는다면 그 오류 값을 최소 손실함수의 값으로 판단하고 그때의 weight값을 최적의 Parameter의 값으로 반환합니다.
저희는 앞에서 손실함수는 weight가 parameter값이라고 배웠습니다. 만약 손실함수의 그래프가 2차원 함수라고 한다면, 최초 W에서부터 편미분을 적용한 뒤 이 미분 값이 계속 감소하는 방향으로 순차적으로 W를 갱신합니다.
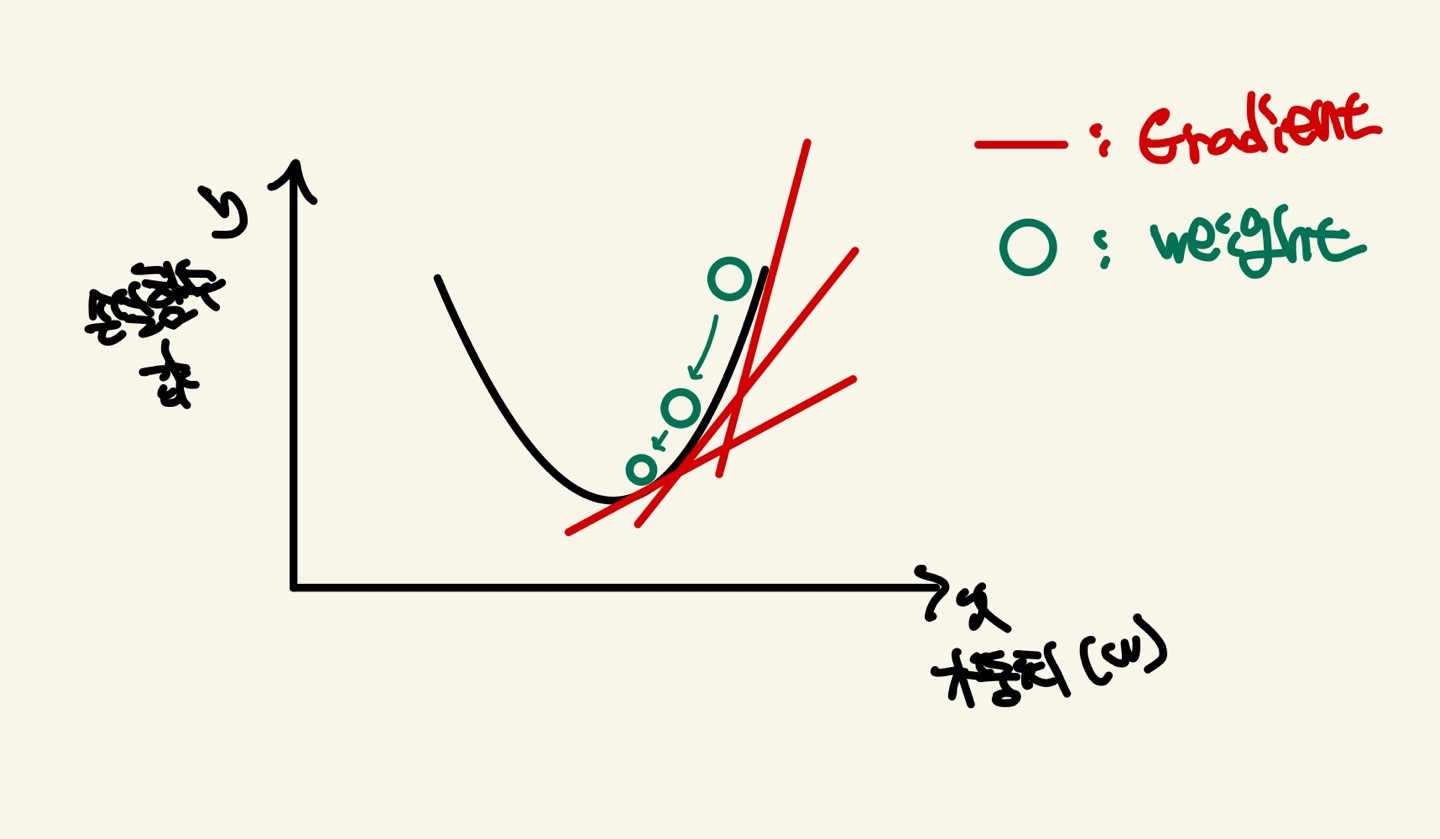
미분을 적용하는 이유는 손실함수의 값은 일단 Weight들로 구성되어 있습니다. 나머지 X(Input Feautures)들은 Constant라고 말씀 드렸죠. 이 손실함수 값을 미분하게 되면 W의 관한 식이 나올것입니다. 이때의 W는 2차함수를 미분했으니 기울기가 됩니다. 이 기울기가 손실함수에서 최소점을 향해서 간다면 손실함수의 값이 작아지게 됩니다.(3차함수이상은 local minimum과 saddle point(안장점)에 빠질 수 있어 다양한 Optimizers들이 나오게 됩니다)
하지만 Weight는 1개의 값이 아니기 때문에 손실함수에서는 편미분을 적용하는것입니다. 그래서 각 Weight들의 편미분값을 구하고 손실함수의 값을 줄이는 방향으로 weight를 갱신하게 됩니다.
(편미분을 하면 input의 weight들의 값이 나오고 그 값들을 줄이는 방향으로 학습한다.)
가중치를 갱신하는 과정에서 학습률(Learning Rate)의 개념이 나옵니다. 이 학습률은 편미분값을 조절하는데 사용합니다. 학습률을 적용하는 이유는 수렴 속도와 최적의 모델 성능을 달성하는데 도움이 되도록 합니다. 단지 편미분값만 이용하면 값이 크기 때문에 weight들의 갱신이 크게 이루어지므로 손실함수의 값이 발산에 가까워질 수 있습니다. 따라서 편미분값에 적절한 학습률을 적용하면 모델이 빠르게 수렴하고 최적의 성능을 달성할수있도록 weight들을 갱신합니다
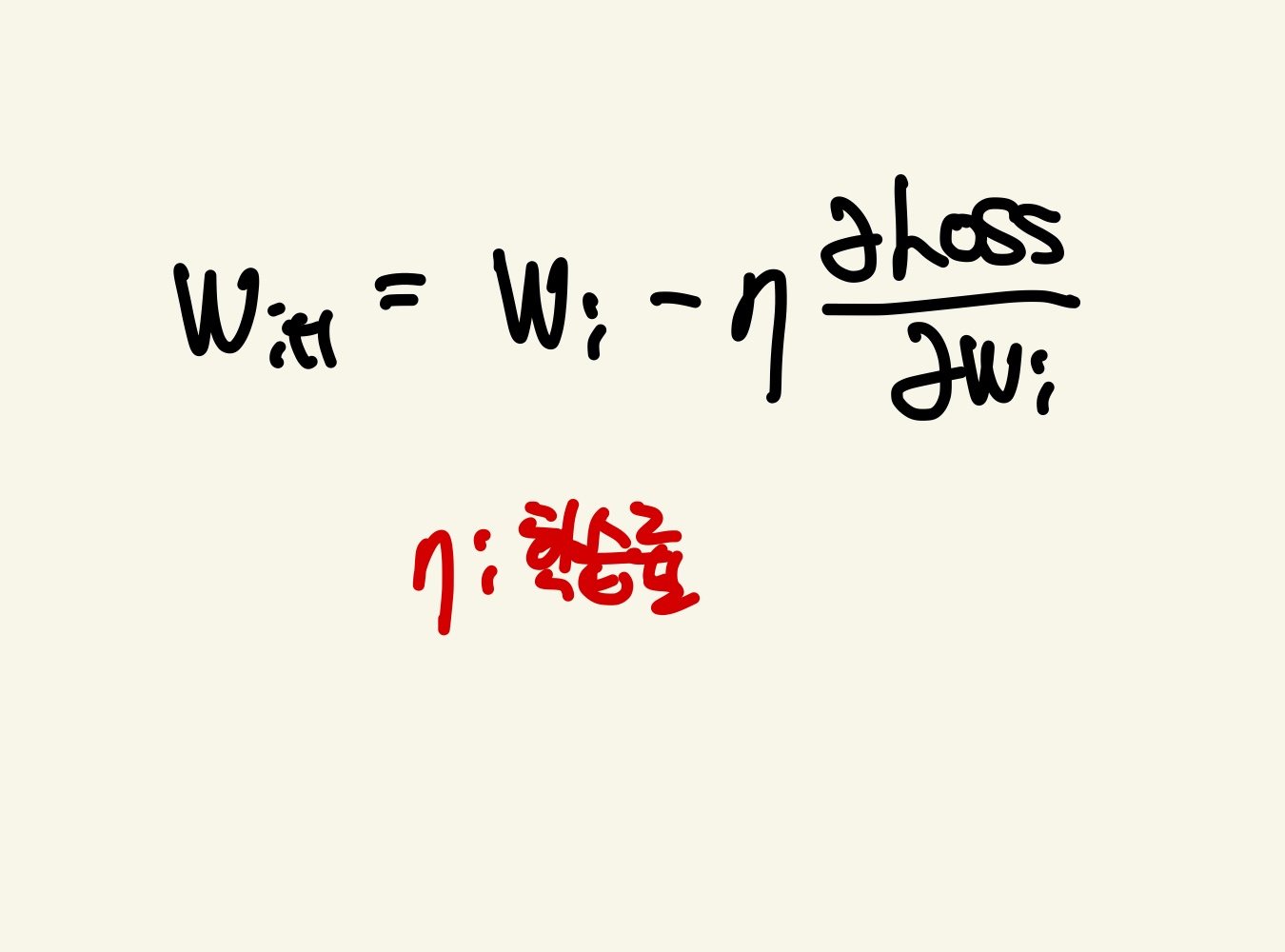
Learning Rate 크기에 따른 이슈
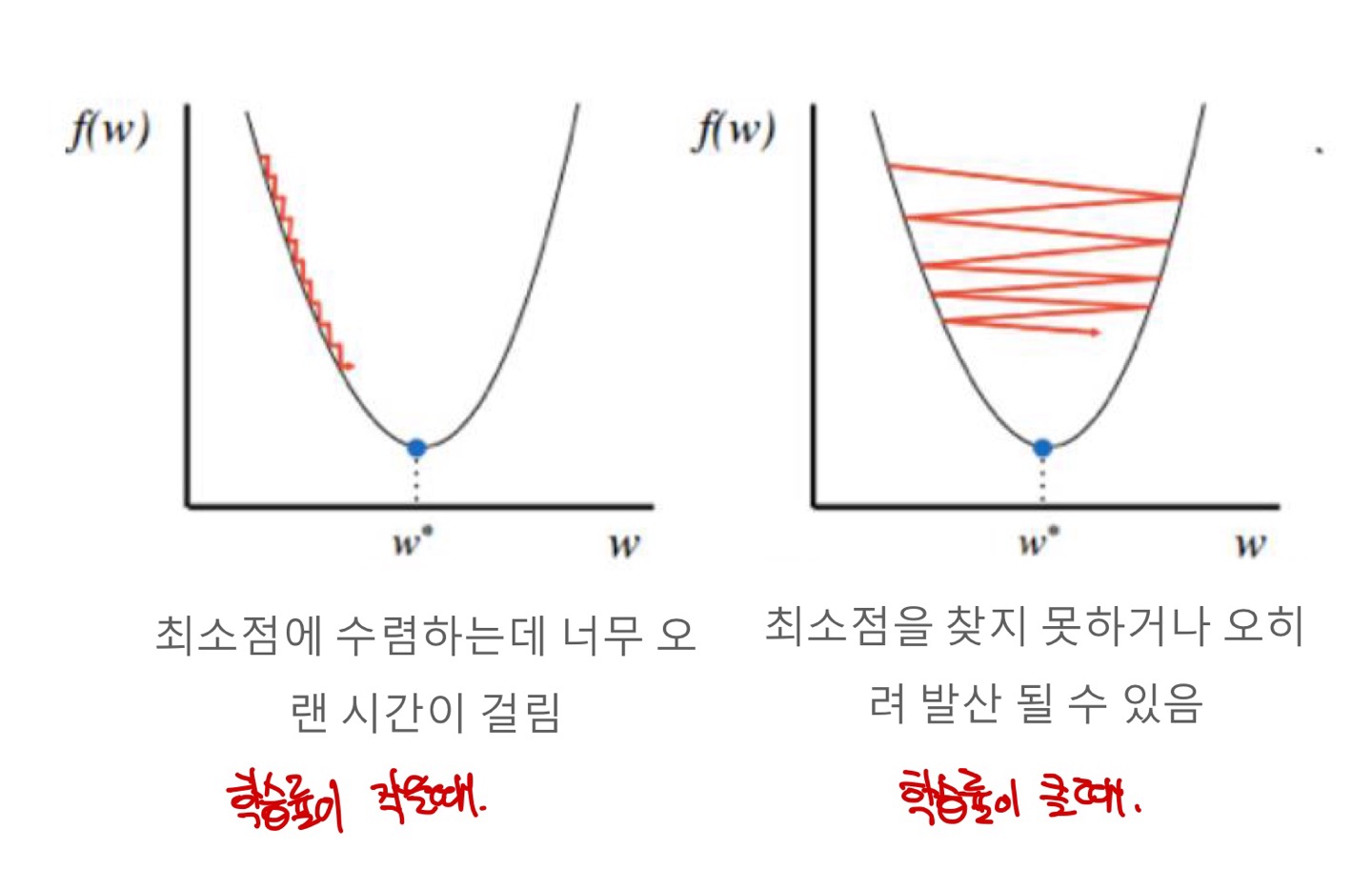
학습률이 너무 작으면 최적의 weight를 찾는데까지 시간이 너무 오래걸리고, 학습률이 너무 크면 최소점을 못찾고 발산할수있습니다. 적절한 학습률을 찾는것이 관건입니다.