S1-WEEK3 Note 02 : Linear Algebra
Warm-up : Linear combinations, span, and basis vectors
-
선형결합
av + bw두 스칼라 중 하나는 고정해놓고 나머지 하나의 값을 자유롭게 놓는다면,
벡터의 머리가 한 직선을 그리게 된다 -
span 선형생성
벡터 v 와 w 의 span : 선형결합의 집합 -
선형종속 linearly dependent
벡터 u가 다른 벡터들의 선형결합으로 표현가능
u = av + bw
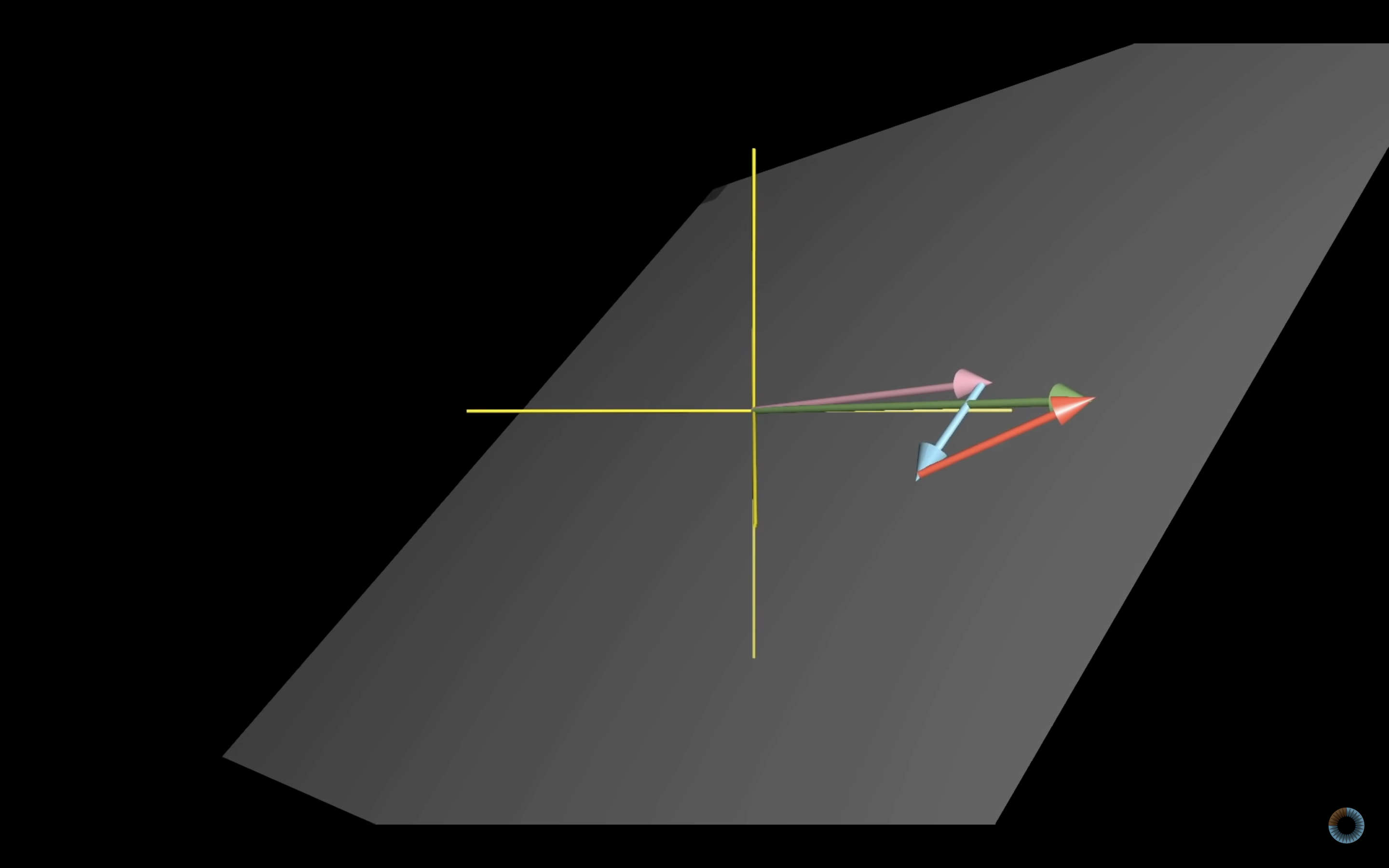ex) 3차원 매트릭스의 세 벡터 중 한 벡터가 선형종속일때
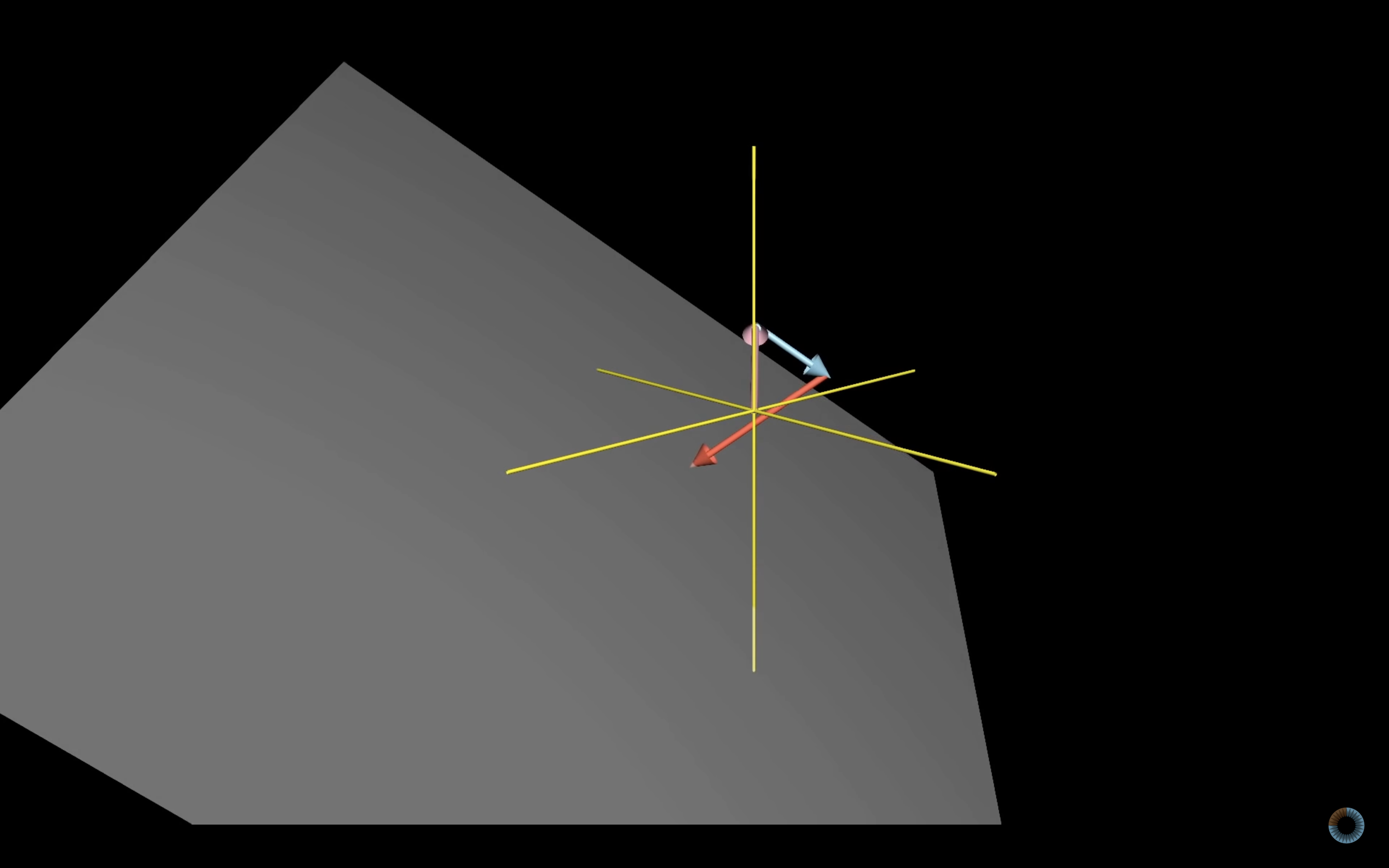ex) 3차원 매트릭스의 세 벡터가 선형독립(linearly independent)일때
- 기저 bias
공간 전체를 생성하는(span) 선형 독립(linearly independent)인 벡터의 집합
Orthogonal Basis : 수직
Orthonormal Basis : 수직,단위 (Gram-Schmidt 프로세스)
Warm-up : Covariance & Correlation
- Covariance (공분산)
(출처 : https://destrudo.tistory.com/15)
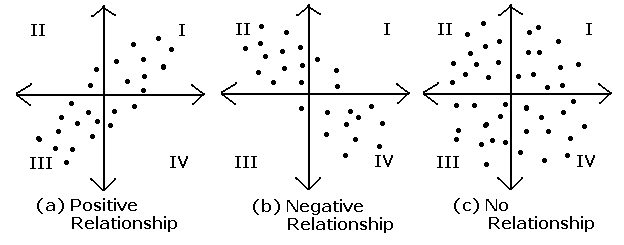
Cov(X, Y) > 0 : X가 증가 할 때 Y도 증가한다.
Cov(X, Y) < 0 : X가 증가 할 때 Y는 감소한다.
Cov(X, Y) = 0 : 공분산이 0이라면 두 변수간에는 아무런 선형관계가 없으며 두 변수는 서로 독립적인 관계에 있음을 알 수 있다. 그러나 두 변수가 독립적이라면 공분산은 0이 되지만, 공분산이 0이라고 해서 항상 독립적이라고 할 수 없다.
확률변수 X의 평균(기대값), Y의 평균을 각각
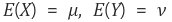이라 했을 때, X,Y의 공분산은 아래와 같다.
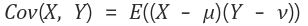즉, 공분산은 X의 편차와 Y의 편차를 곱한것의 평균
간단히 표현하면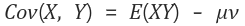 
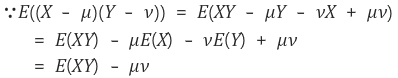X와 Y가 독립이면
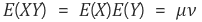이므로 공분산은 0이 된다.
- Correlation(상관계수)
공분산의 문제점 = X와 Y의 단위의 크기에 영향을 받는다
-> 보완하기 위해 상관계수
공분산을 두 변수의 표준편차로 나눠줌
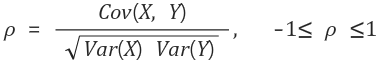-> 확률변수 X, Y가 독립이라면 상관계수는 0
-> X와 Y가 선형적 관계라면 상관계수는 1 혹은 -1이다.
(양의 선형관계면 1, 음의 선형관계면 -1)
-> 상관계수는 데이터의 평균 혹은 분산의 크기에 영향을 받지 않는다
Variance-covariance matrix
df.cov()공분산 matrix의 대각선 부분은 공분산이 아닌, 분산을 표현
Spearman correlation (categorical)
값들에 대해서 순서 혹은 rank를 매기고, 그를 바탕으로 correlation을 측정하는 Non-parametric한 방식
<-> Pearson correlation (numeric) : correlation, coefficient
- Non-parametric : 비모수통계 (https://ko.wikipedia.org/wiki/%EB%B9%84%EB%AA%A8%EC%88%98_%ED%86%B5%EA%B3%84)
Variance (분산)
- 모집단의 분산
모집단의 PARAMETER (aspect, property, attribute, etc)
# ddof는 자유도
df.v1.var(ddof = 0)- 샘플의 분산
샘플의 STATISTIC (estimated attribute)
df.v1.var(ddof = 1)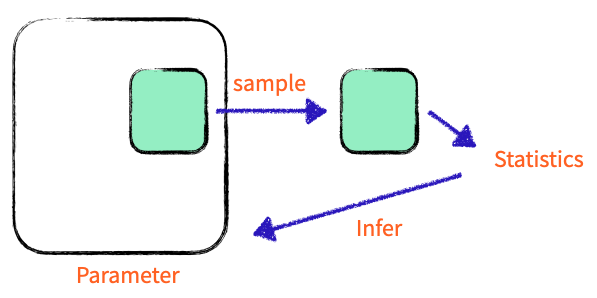
샘플분산 은 모집단 분산 의 추정치
샘플 분산 계산시 로 나눠야함
Orthogonal
좌표상에 있는 거의 모든 벡터는 다른 벡터와 상관이 아주 작게라도 있음
-> 공분산, 상관계수 계산 가능
서로 수직인 벡터는 상관 관계가 없다
Gaussian Elimination
주어진 매트릭스를 "Row-Echelon form"으로 바꾸는 계산과정
- Row-Echelon form : 각 행에 대해서 왼쪽에 1, 그 이후 부분은 0으로 이뤄진 형태
Linear Projection (사영)
Feature을 줄이는 과정에서 data loss (information of feature)
data 저장하기 위한 메모리 줄일 수 있음
