Least Squares

최소제곱법으로도 불리는 방법은 linear regression을 배웠다면 이해하기 더 쉬운 것 같습니다. 먼저 over-determined부터 알아보겠습니다.

Over-determined

과결정이라고도 불리는 이것은 선형방정식에서 주어진 방정식의 개수가 미지수의 개수보다 많을 때, Over-determined라고 부릅니다.

$e.g.$ $A^{100,3}$$V^{3,1}$ 이런 경우 일반적으로 해가 존재하지 않게 되겠죠?

위와 같은 경우 3개의 변수로 100개의 방정식을 모두 만족시키긴 어려울테니까요.
이러한 문제를 해결하기 위해 근사적으로 해를 구하는 것입니다! 그것이 Least squares!

Least Squares

$Ax\neq b$ 라서 구할 수 없으니 근사한 $A\hat{x} = \hat{b}$ 을 찾는 방법.

먼저 존재하지 않는 해에 대해서 근사적으로 해를 찾는 방법이니까 당연하게도 $A$라는 matrix 안에는 값이 존재하지 않겠죠. 또, 근사적, 그러니까 가장 가까운 값을 찾는 것이니까 다른 길이에 비해 가장 짧아야 합니다.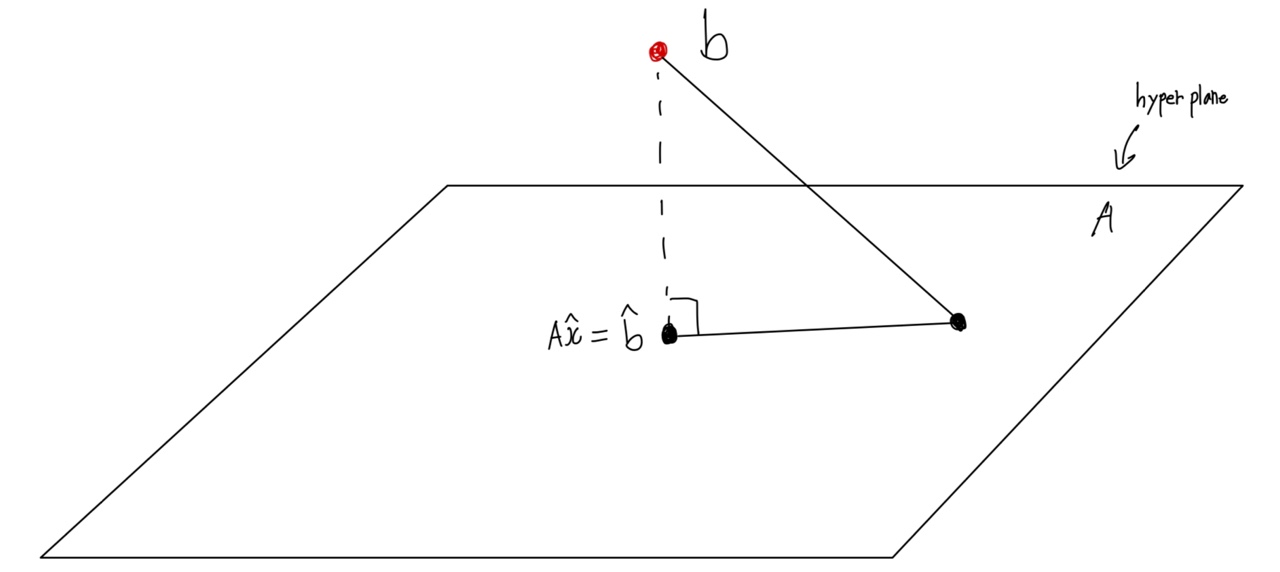
위 그림에서 점선으로 표시한 부분은 $b-\hat{b}$입니다. $\hat{b}= A\hat{x}$이니까 $b-A\hat{x}$로 표현할 수 있습니다. 수직인 값은 내적했을 때 0이기 때문에 $(b-A\hat{x})\perp A$ 여기서 A는 수직인 column들 입니다.

Normal equation

$A^T(b-A\hat{x})=0$이며 풀면 $A^TA\hat{x}=A^Tb$가 되는데 이것을 normal equation이라 부릅니다.

그리고, 역행렬이 존재할 때 다음과 같이 풀 수 있습니다.

역행렬이 존재하지 않는다면 pseudo-inverse (유사 역행렬) 무어펜로즈 역행렬 $A^+$을 이용할 수 있고, 유사 역행렬은 아래에 적어두겠습니다.
역행렬이 존재하지 않는 경우는 Linear dependent한 경우에 해가 무수히 많거나 아니면 아예 존재하지 않는 경우인데 해가 존재하지 않을 경우는 있다고 보기 어렵기 때문에 해가 무수히 많을 경우만 생각하면 될 것 같습니다. Over-determined 된 상황이니 아무래도 Linear dependent한 경우는 적을 것 같습니다.

Pseudo-inverse

$n \geq m$인 경우

$n \leq m$인 경우