Linear Algebra

선형대수학을 공부했던 내용을 정리하고 기록하려고 합니다. 제가 이해했던 것들을 위주로 적기 때문에 틀리거나 부정확한 것들이 있을 수 있습니다. 😢 그럼 시작하겠습니다!! > Linear dependence와 independence 구별 선형 독립과 선형 종속

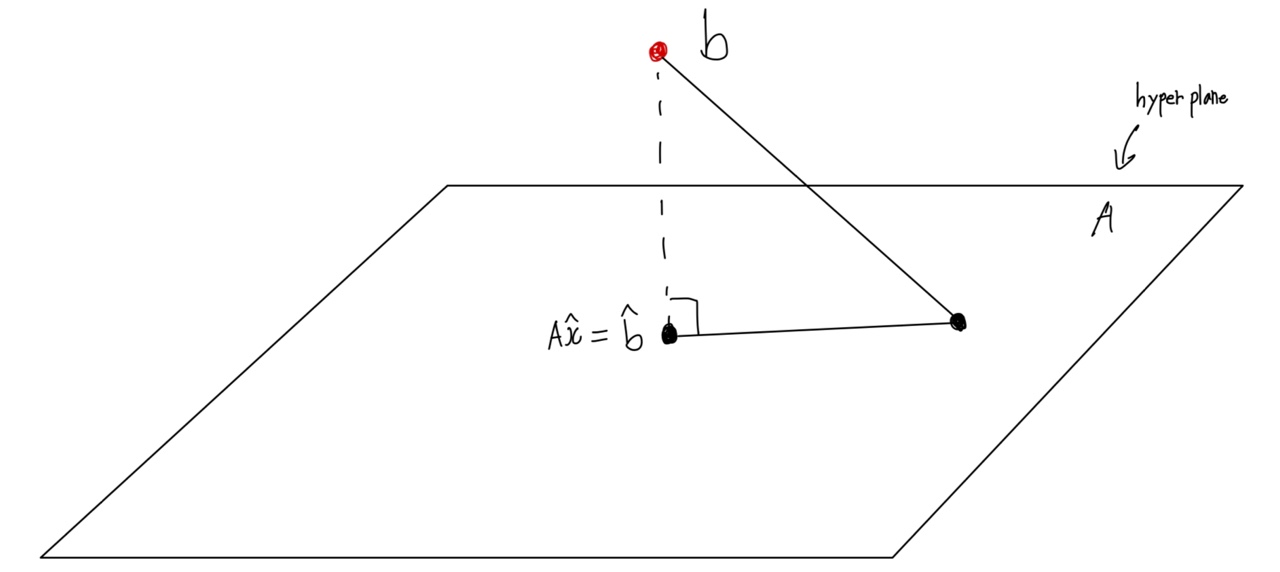
항상 공부하지만 쉽지 않습니다,,알면 알수록 더 깊은 학문이네요 머리로 이해는 했지만 글로 쓰려니 더욱 찾아보고 오히려 더 공부하는 느낌이 듭니다..🥲 그럼 시작하겠습니다!😇 Least Squares 최소제곱법으로도 불리는 방법은 ml- linear regress

orthogonal = 직각, 직교의 projection = 사영,투영,투사

Gram-Schmidt Orthogonalization 그람슈미츠는 임의의 벡터들로 orthogonal한 벡터들을 구하는 과정입니다. 임의의 다른 벡터 4개가 존재한다고 가정하겠습니다.(Linear independent, non-orthogonal) $a1, a2

Eigen Value Decomposition으로 고유값 분해라고 한다.수식으로 조금 더 쉽게 다가가보자 A$\\vec{v_1}$ = $\\lambda_1$$\\vec{v_1}$A = matrix, $\\vec{v_1}$=eigen vector, $\\lambda$=e

이전 포스팅이였던 EigenDecomposition의 한계점을 해결할 수 있다.square matrix(nxn), symmetric matrix, 두가지 단점이 있었습니다.$$A=U\\Sigma V^T$$위 수식이 SVD입니다 $U=(n,n),V=(m,m), \\Sig