이번 포스터에서는 importance sampling에 대해 알아보겠습니다!
MC, Sarsa의 경우느 target policy와 behavior policy가 같은 on policy입니다.
이 경우 behavior policy를 임의적으로 다르게 하여 off policy로 만들 수 있습니다.
이것이 importance sampling입니다.
MC sampling을 통해 식을 변경할 수 있고, MC이기에 N을 충분히 크게 잡으면 근사하게 됩니다.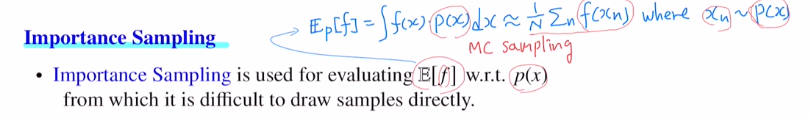
만약 p(x)에서 샘플링하는 것이 어렵다면? unifrom 분포나 가우시안 분포면 샘플링하기 쉽습니다. 따라서 q(x) 여기서 샘플링을 하는데, 조정을 하게 됩니다. p(x)/q(x)를 곱해주며 이를 조정해줍니다. 이것을 importance weights라고 합니다.
(여기서 조건은 p(x)>0이면 q(x)>0으로 잡아줍니다.)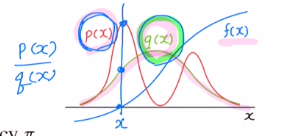
그럼 아래와 같이 바뀝니다. 이것을 importance sampling이라고 합니다.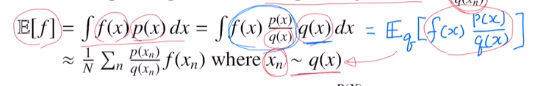
아래는 discrete의 경우입니다. 이도 마찬가지로 P분포를 따르는 것에서 Q분포를 따르게 하고 weight를 곱해주어 변형했습니다.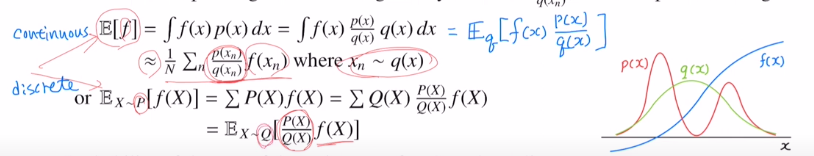
아래와 같이 곱의 형태로 바꿀 수 있고, Gt return값 하나하나 마다 아래의 확률로 return값이 발생합니다. 위의 f가 Gt역할을 하는 것이고, P가 파이 역할을 하는 것 입니다.
위 사진에서의 곱들이 Gt에 가야하는 것인데, 이제는 on policy가 아닌 off policy를 사용하기 위해 아래와 같이 importance sampling ratio를 통해 바꿔줍니다. q가 behavior policy가 된 것 입니다! data sampling을 q에서 하기 위해 아래와 같이 바꿔줍니다. 이제는 π(이전의 p)라는 target policy가 아닌 μ(이전의 q)라는 behavior policy를 사용하게 됩니다. 여기서 transition pobability가 상쇄되기에 model free인 강화학습에서 사용할 수 있는 것 입니다!

MC와 TD의 sarsa를 off policy로 바꿔줍니다.
원칙적으로는 target이 있고, 이 target을 결정하는 것이 target policy이며 target policy를 위한 value들을 estimate해야 하는데(target policy π에서 만들어진 샘플들에서 reward를 가져와야 합니다.),
μ라는 새로운 에피소드를 만들어 여기서 return값을 가져와 사용합니다.
behavior policy μ에서 가져온 return값에 importance weight을 곱해서 target policy π에서 얻어진 return값으로 이해하는 것입니다.
Temporal Difference Learning에는 한 term만 곱해주면 됩니다.
이렇게 on policy를 off policy로 importance wegiht를 곱하여 바꿔줄 수 있습니다.
추가적으로 variance가 MC에서 사용할 때 곱으로 인해 엄청 커집니다. 즉, target을 볼 때 요동친다는 것이기에 converge 속도가 느려집니다.
이제는 Bias 와 Variance를 알아보겠습니다.
true value q, estimator Q가 있을 때 아래와 같이 말할 수 있습니다. 둘 다 작을 수록 conv 속도가 빠르고 좋습니다.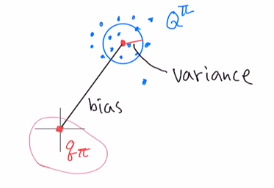
MC는 Gt가 unbiased이지만, TD에서는 estimator Q를 사용했기에 편향이 생길 수 밖에 없습니다.
TD는 한 스텝 마다 random성이 있습니다. MC는 전체에 대해 랜덤성이 계속 작용한 것이기에 MC의 분산이 더 클 수 밖에 없습니다.
MC vs TD
둘 다 unknown MDP입니다.
MC는 return을 사용하기에 무조건 에피소드 끝까지 가야합니다.
TD는 다음 스텝만 주어져도 학습 가능합니다.
TD는 Markov property에 예민합니다. 이를 잘 만족해야 합니다.
MC는 큰 영향을 받지 않습니다.
초기화에 대해 MC는 어차피 게임 끝까지 간 후 return을 얻지만 TD는 그렇지 않기에 초기화에 대해 영향을 더 받습니다.
MC : higt variance, zero bias
TF : low variance, some bias
둘 다 policy improvement로 conv하긴 하지만 수학적으로는 어느 것이 더 빨리 conv할지는 불명확합니다. 보통은 TD가 빠르긴 합니다. 효율성도 TD가 끝까지 가지 않기에 좋습니다.
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=1BcEwmxSr8E&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=14
