이번 포스터에서는 강화학습에 관련된 몇 가지 예시와 sarsa와 q learning을 변형한 알고리즘을 알아보겠습니다.
A에서 B로 갈 때 reward=0입니다. B에서 terminal state로 갈 때는 두 가지 종류로 나뉘어 1 or 0을 얻을 수 있습니다. 확률은 unkown MDP이기에 transition prob는 모르는 상황입니다.
여기서 샘플링을 통해 action은 고려하지 않고 8개 에피소드를 얻었습니다.
아래를 보시면 한 경우만 A에서 시작하고 나머지는 모두 B에서 시작했습니다.
이들을 가지고 A에서의 state value값, B에서의 state value값을 예측하고자 합니다. 하나는 TD을 사용하는 방법과 MC를 사용하는 방법이 있는데 어느 것이 더 좋은 예측을 했는지 비교해보겠습니다.
우선 state B에서 시작하는 경우를 보겠습니다. 두 개는 0이고 나머지 6개는 1을 얻었기에 return 기댓값은 0.75가 됩니다. 여기서는 어차피 B에서 terminal로 가는 한 스텝밖에 없기에 TD나 MC나 똑같습니다. 그렇기에 둘 다 V(B) = 0.75 가 됩니다.
이제 A를 고려해보겠습니다.
TD에서는 Rt+1=0, next state V(B)=0.75, 감마=1
V(A) = 0.75
MC에서는 현재 A에서 시작하는 샘플은 하나밖에 없기에 Gt=0입니다.
V(A)=0
A에서 시작하는 데이터가 하나밖에 없기에 이런 경우가 생깁니다. 이런 경우는 TD가 더 괜찮다고 생각할 수 있습니다.
MC는 주어진 데이터에 아주 예민하게 반응합니다.
그렇기에 만약 8개 이외의 데이터를 많이 생성하면 TD에 더 적합합니다.
이번에는 Sarsa와 Qlearning에 대해 알아보겠습니다.
Sarsa는 입실론 그리디를 사용하여 action을 선택하기에 near하게 접근합니다.
하지만 Qlearning은 바로 maximize하는 action을 선택하기에 optimal 값을 바로 선택하는 것 입니다.
우선 Cliff walking에 대해 알아보겠습니다.
한 스텝 당 reward -1점이 부여되고 cliff로 들어가면 큰 벌점(-100)을 받습니다.
이 때 optimal path는 당연히 하나 올라갔다 직진 후 내려오는 것 sum of rewards = -13을 얻는 것이 optimal path입니다. 보통은 Qlearning이 sarsa보다 성능이 좋게 나오지만, 이 경우는 sarsa가 더 좋게 나옵니다.
왜 Q learning은 성능이 좋지 않을까요?
highest Q value를 갖는 action인 그 때의 optimal 을 봅니다.
학습을 할 때는 target policy를 염두에 두고 있고, 실제 데이터를 생성하고 액션을 취할 때는 behavior policy로 행동하는 것 입니다.
Sarsa는 머리속으로 ε-greedy 방법을 사용하고 실제로도 ε-greedy 방법을 사용합니다.
하지만 Q learning은 highest Q value를 찾는 action을 선택하는 greedy 방법 생각하지만, 실제로는 ε-greedy 방법을 사용합니다.
그렇기에 Sarsa는 애초에 ε만큼 다른 방향으로 갈 위험을 염두에 두고 있습니다. 그래서 왠만하면 cliff와 멀리 돌아서 가려고 합니다. 하지만 Q learning은 생각을 애초에 greedy로 하고 있기에 고려하지 않습니다. 그래서 이전에 이야기 했던 optimal path로 움직입니다. 하지만 실제로는 ε만큼 cliff방향으로 갈 수 있기에 위험에 많이 빠지는 것 입니다. 따라서 성능이 여기서는 Sarsa가 더 좋게 나옵니다.
총 1/40만큼 cliff에 빠집니다. 13칸을 3번 정도 하면 40칸 정도이니, 게임을 세 번할 때 한 번은 cliff에 떨어지게 되는 것으로 생각할 수 있습니다. 즉, 한 번 게임할 때 -100/3인 -33점을 받을 확률이 있다고 생각할 수 있습니다. 따라서 평균적으로 -13-33 = -46 정도를 받게 됩니다.
입실론 값이 점점 줄어들면 Qlearning이 더 좋아지게 될 것 입니다.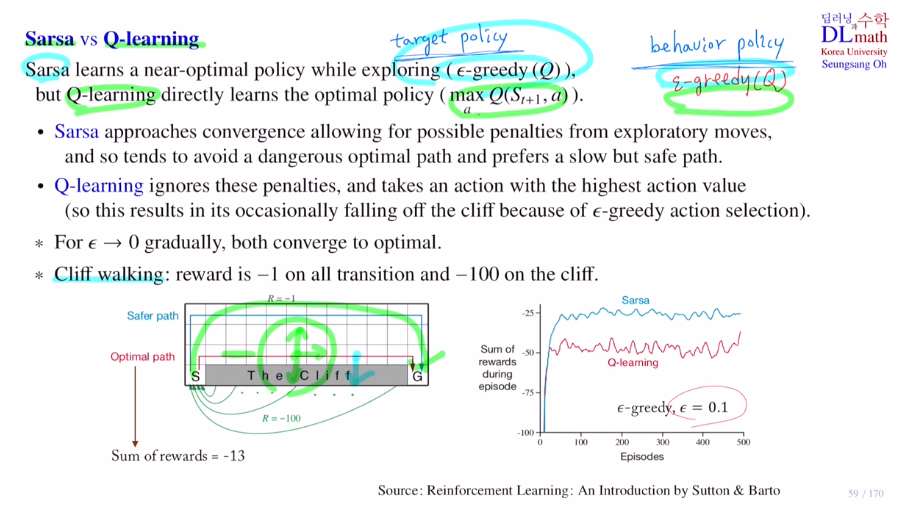
이번에는 Sarsa의 단점을 보완한 expected Sarsa에 대해 알아보겠습니다!
Sarsa : (s,a,r,s',a') : ε-greedy 확률분포에서 선택
Q-learning : (s,a,r,s') : highest Q value값을 갖는 action 하나 선택
Expected Sarsa : (s,a,r,s',a') : 위 두 개의 기댓값. 그렇기에 Qlearning과 비슷하지만 모든 action을 고려했다는 점이 차이가 있습니다. 하지만 기댓값을 구해야 하기에 당연히 계산량은 늘어납니다.
이번에는 Double Q-learning입니다.
target에 highest Q value를 계속 취하기에 반복적으로 높은 값을 취하게 됩니다.
이렇게 되면 과대적합 오버피팅이 일어날 수도 있습니다. 그렇기에 maximize operation은 오버estimate가능성이 있고, convergence가 더디어 집니다.
여기서는 두 개의 Q 테이블을 사용합니다. Q1은 maximizing action을 사용하는 것이고, Q2는 policy evaluation을 위해 사용합니다.
이렇게 되면 Q1에서는 highest Q value를 갖는 action을 취하지만 Q2에서는 그렇지 않을 수 있게 됩니다. 이렇게 하여 Q value값을 낮춰주는 경향이 있습니다.
교대로 업데이트 합니다.
여기서는 ε-greedy in Q1+Q2 입니다.
이번에는 TD의 확장판인 TD(λ) 를 알아보겠습니다.
TD target과 MC target 의 중간 단계인 n-step return이 있습니다.
어떤 경우는 게임이 끝날 때까지 가는 것이 유리할 때가 있고, 어떤 경우에는
바로 next state을 이용하여 한 step마다 진행하는 것이 유리할 때가 있습니다.
n-step return은 이 둘을 적절히 융화한 것으로 원하는 곳 까지 보는 것 입니다.
TD(n)은 n-step Temporal Difference learning입니다.
모든 state를 사용하기 위해 모든 것들을 더해줍니다.
이것이 λ-return 입니다.
discounted vector λ를 통해 조절을 해줍니다. λ가 0에 가까우면 가까운 것을 중요하게 보고, 커지면 골고루 보게 됩니다.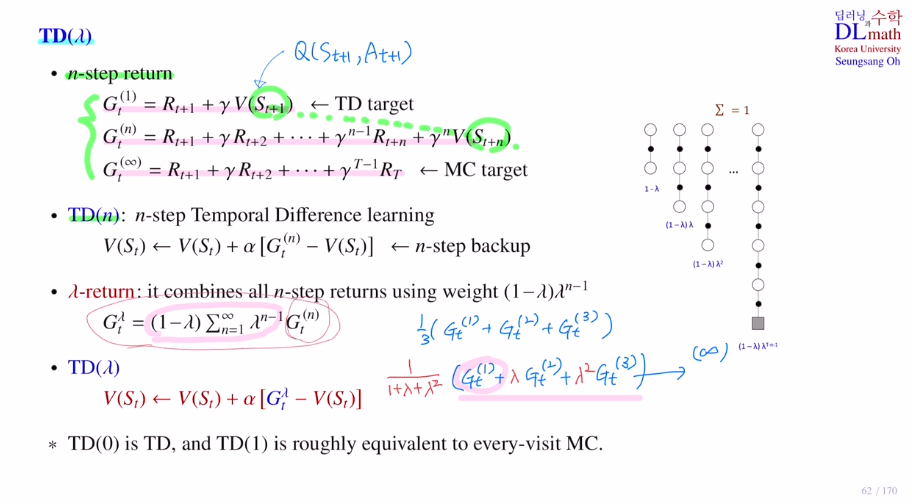
이 λ-return을 가지고 target으로 해서 만든 TD 방법이 TD(λ) 입니다.
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=g7JnA_ArmOU&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=15
