이번 포스터에서 다룰 내용은 Markov Decision Process로 마르코브 의사결정 과정이라고 합니다!
이 마르코브 의사결정 과정을 잘 설명할 수 있는 Grid world라는 모델을 소개하겠습니다.
이 모델은 Dynamic programming과 Reinforcement Learning에 자주 등장하는 모델입니다.
그리고 Markov Decision Process의 핵심인 Markov property에 대해 알아보겠습니다.
먼저 Grid world example을 확인해보겠습니다.
이는 Markov Decision Process가 잘 적용되는 예시 모델입니다.
4x3 grid (한 칸은 벽)
robot = agent = 강화학습을 통해 스스로 학습하는 컴퓨터, 즉 학습의 주체
이 grid world 안에서 robot이 살아갑니다.
agent는 동서남북 방향으로 한 칸씩 action을 취합니다.
start라는 (1,1) state에서 출발하여 action을 취해 한 칸씩 이동하게 됩니다. 최종 (4,3) or (4,2)에 도달하면 게임이 끝납니다. 중요한 것은 어디에 도착하느냐에 따라 보상이 달라집니다.
따라서 각 state마다 어디로 움직일지 잘 정해서 (4,3)에 도달하기를 원합니다.
agent가 좋은 점수를 가지고 게임을 마치기 이해서는 reward를 주어 reward를 높이는 방향으로 학습을 합니다. 따라서 이 보상을 정해주어야 합니다. 이 경우에는 두 가지 종류의 보상이 있습니다. 하나는 big reward라는 (4,3)도달 승점(good +1)과 (4,2)도달 벌점(bad -1)이 있습니다. 다른 하나는 small negative reward로 만약 (1,1)<->(2,1)로 반복하며 게임이 끝나지 않는 경우가 생길 수도 있는데 이 의미없는 행동을 막기 위한 방법으로 action 한 번 취할 때 마다 약간의 감점을 주는 것 입니다. 예를 들어 c=-0.1이라고 한다면 한 번 action할 때 감점이 됩니다.
((4,2)or(4,3)에 도달할 때는 따로 c를 주지 않습니다.)
이 Grid world에서 핵심적인 내용은 agent가 항상 계획적으로 움직이지 않는다는 점입니다.
이를 noisy movement라고 합니다.
예를 들어 agent에게 action으로 north로 취한다고 했는데, 실제 환경에서는 약간의 노이즈가 있기 때문에 west로 갈 수도 있다는 것 입니다.
따라서 아래를 보면 action을 north로 취해도 80%는 가지만 10%는 west, 10%는 east로 취합니다. (아예 정반대로 가지는 않습니다.)
즉, 실제 결과에는 random성이 있다는 것입니다.
하나의 state에서 다른 state로 움직이는 것을 state transition이라고 하는데, 이 때 확률이 적용되는 것 입니다. 이 확률을 state transition probability라고 합니다.
Grid world는
State(11개) / Action(4개) / Reward(2가지) / State transitoin probability
네 가지 요소로 구성되어 있습니다.
추가적으로 만약 (1,2)에서 east or west로 이동하려 한다면?
이 벽이 있는 경우는 가만히 있게 됩니다.
이제 게임을 시작하겠습니다. 한 게임을 Eposode라고 합니다.
아래와 같이 이동한 경우 총 5번을 움직였고(마지막 제외), (4,3)에 도착하였기에 이 에피소드에서 Total reward는 5c+1이 됩니다.
강화학습에서 하고 싶은 목표는 에피소드가 한 번 진행될 때 마다 total reward를 최대화하는 것입니다. 즉 각 state마다 action을 잘 정해주어 total reward를 maximize하는 것이 목표가 됩니다. 각 state에서 어떤 action을 취하는 것이 좋을지 를 정하는 policy를 잘 세워야 합니다. total reward를 maximize하는 policy를 optimal policy라고 하며 이 optimal policy를 찾는 것이 강화학습의 핵심 목표입니다!
Grid world에서 action을 정하는 방법이 두 가지가 있는데 이를 살펴보겠습니다.
Deterministic grid world
agent의 action을 north로 취했다면 노이즈가 따로 없이 north로 결정적으로 100%로 이동합니다.
: policy가 정해지면 one eposode
Stochastic grid world
agent에 north라는 action을 취하면 10% 80% 10%로 확률을 가지고 움직입니다.
동일한 state and action이 있지만 다른 output이 나올 수 있는 것입니다.
이렇게 랜덤성이 적용되는 것 입니다. (대부분은 이 Stochastic 방법을 사용합니다.)
: policy가 정해지면 many episodes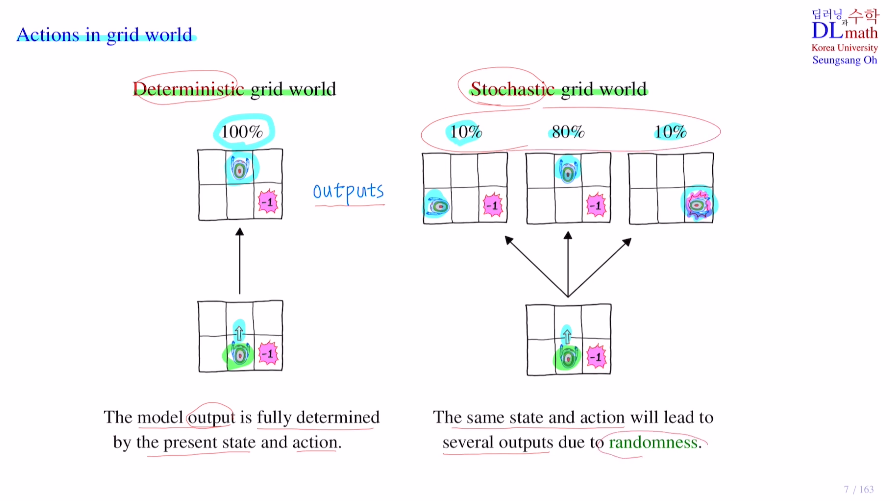
이번에는 Markov Decision Process의 핵심인 Markov property에 대해 알아보겠습니다.
Stochastic or random process라고 하는데 이것의 정의부터 살펴보겠습니다.
여기서 random variable이 나오는데 확률을 표현할 때 P(X=3) 여기서 X를 random variable이라고 하며 이 random variable X가 3이 될 확률을 말합니다. 여기서는 확률변수 하나를 다루는 것이 아니라 확률변수의 collection을 다룰 것 입니다. 이를 Stochastic process라고 말합니다.
Stochastic process에서는 확률변수의 컬렉션이 있으면, 이것을 index를 줄 수 있는데 주로 time set으로 합니다. 보통은 X를 사용하지만 저희는 강화학습을 다루기에 state을 나타내는 S0,S1,S2,...,St,..를 사용하겠습니다.(St:present state)
그리고 t라는 인덱스는 time(1초,2초,..)이라고 생각하겠습니다.
여기서는 각각을 1,2,3초 처럼 나눌 수 있으면 discrete time random process(이산확률과정)라고 하며,
연속적인 것을 continuous time random process(연속확률과정)라고 합니다.(보통은 이산확률과정을 생각합니다.)
마치 시퀀스처럼 표현되는 이것을 Stochastic or random process라고 합니다.
확률 과정이라고도 합니다.
Stochastic process {St} 가 있을 때, Markov property를 만족하면 이 Stochastic process를 Markov process(or Markov chain) 라고 합니다.
Markov property
공의 움직임을 예측할 때, 이전 past state들을 알고 있다면 다음 next state을 예측하기 쉽겠지만 현재 state만 알고 있다면 어디로 갈지 예측하기 어려울 것 입니다. 즉, future state는 past state에 영향을 받는다고 할 수 있습니다. 하지만 만약 질량이 0에 가까운 미세먼지라면 관성의 법칙을 받지 않아 어느 방향으로도 갈 수 있습니다. 더 이상 past state에 영향을 받지 않는 것 입니다. 이런 운동을 Brownian motion이라고 합니다.
Markov property를 가졌다는 것은 이렇게 next state로 이동할 때, past state이 present state에 전혀 영향을 미치지 않는 것을 말합니다.
P(St+1=s'|St=s) = P(St+1=s'|S0=s0,S1=s1,...,St=s) 이라는 것 입니다.
Stochastic process가 Markov property를 가지면 Markov process(or Markov chain)라고 하는 것 입니다.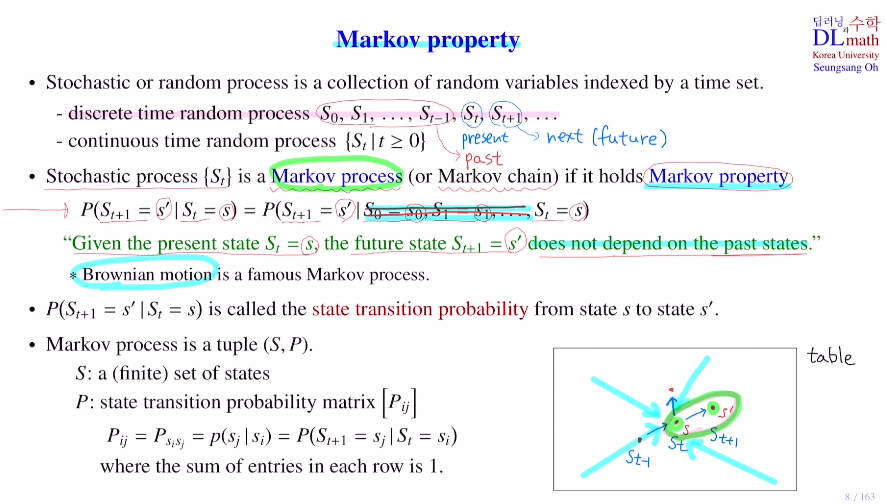
Stochastic process가 Markov property를 갖는다는 것은 엄청난 장점이 있습니다.
왜냐하면 다음 state을 예측할 때 만약 Markov property를 만족하지 않는다면, past state에도 depend하기에 이전 past state에 대해 정확히 알고 있어야 계산이 가능합니다. 이전 state을 다 기억해야 하고, 복잡한 조건부확률을 계산해야 합니다.
따라서 Markov property를 만족하면 현재 state만 알고 있으면 되는 것이기에 훨씬 확률을 계산하는데 효율적입니다.
Markov property : memoryless property
Markov process는 두 가지로 이루어져 있습니다. (S,P)
S : a (finite) set of state
P : state transition probability matrix [Pij]
아래의 예시를 보면 S = {S1,S2,S3} 이고 이에 따른 확률은 아래와 같은 matrix로 나타납니다.
(matrix에서 각 row sum은 1이 됩니다.)
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=EtSNMoM97-k&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=2
