오늘 다루어 볼 내용은 Markov Decision Process MDP : 마코프 의사결정 과정 이라고 합니다!
MDP는 강화학습을 구현하는 기본적인 수학적 확률 모델입니다.
Stochastic process {St}는 random variable의 컬렉션이라고 하는데 이것을 시간에 대한 시퀀스로 생각해도 괜찮습니다.
(St: present state)
여기서는 St->St+1로 갈 때의 확률이 중요합니다. 여기서는 Markov process를 따르기에 확률을 쉽게 구할 수 있게 됩니다.
이제 MDP에 대해 이야기 해보겠습니다.
여기서는 5개 piar로 되어 있습니다. (S,A,P,R,γ)
모든 state에서 Markov property를 만족해야 합니다.
Markov process (S,P)에서 추가로 action과 reward가 추가되었다고 생각하면 됩니다.
S : state space
A : action space
P : state transition p from s to s' given a (여기서는 s에서 조건부 action이 취해진 후 s'을 의미합니다.)
R : reward function : 현재 state s에서 action a를 취했을 때 s'이 얻어질 때의 reward
reward가 주어지는 방법은 세 가지로 1) 어떤 특정 state에 있으면 reward가 주어지는 경우와 2) 현재 state에서 action을 취하자 마자 reward가 주어지는 경우와 3) s에서 action을 취하고 s'이라는 next state에 도착해야만 주는 reward
γ : discount factor로 감가율이라고 합니다.
아래의 그림을 예시로 들면 세 개의 state이 존재하고 두 개의 action a0,a1이 있습니다. reward는 두 가지로 1or-1이 있습니다.
여기서 가장 중요한 것은 파란색 숫자인 P:transition probebility입니다. 현재 state에서 action이 취해지고 다음 state로 갈 확률 입니다.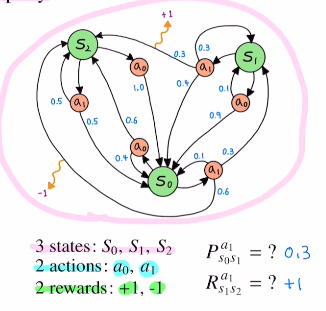
이제부터 많이 쓰일 말이 있는데,
Model-based : known MDP 와 Model-free : unknown MDP입니다.
어떤 모델은 P를 구할 수 있을 수도 있고 구하는 것이 어려울 수도 있습니다.
MDP에서의 Environment model(환경모델)은 transition probability를 말하겠습니다. 이 transition probability를 알고 있으면 모델을 기반으로 해결할 수 있기에 Model-based라고 하며 모르면 Model-free라고 합니다.
Model-based의 해결방법
Model-based의 경우 모든 transition probabiliy를 알고 있는데, 확률의 개수가 상당히 방대함으로 이를 풀어가는 방법 중 하나가 Dynamic programming입니다. 이 Dynamic programming은 효율적으로 풀 수 있게 해줍니다.
Model-free의 해결방법
transition probabiliy를 모르기에 샘플 데이터를 기반으로 policy를 계산하게 됩니다. 여기서 쓰이는 방법이 강화학습입니다.
이번에는 grid world에서의 MDP를 알아보겠습니다.
총 11개의 state로 이루어진 State set이 있고, action은 네 종류가 있습니다.
grid world는 Stochastic grid world를 쓰기에 action을 north로 취했지만 확률적으로 움직이기에 다른 방향으로 갈 확률도 있습니다.(N0.8 E0.1 W0.1) 이들이 state transition probability가 되는데 여기에서는 현재 state 9개, 취할 수 있는 action 4가지, next state는 11가지(?) 로 396가지의 transition probability가 나옵니다.
big reward는 (3,3)-eat->(4,2) +1점 , (3,2)-north->(0.1확률로 east이동 4,2) -1점, ... 등의 경우들이 있습니다.
small negative value 로 움질일 때마다 -0.1로 감점을 주는 것도 있습니다.
(이 c에 따라 달라지기에 적절히 설정하여 optimal policy를 잘 찾는 것이 목표입니다.)
여러가지 c를 주며 어떻게 바뀌는지 확인해 보겠습니다.
아래는 네 가지 모델이 있는데 이 중 가장 좋은 모델을 찾아보겠습니다.
(c = -0.01, -0.03, -0.4, -2)
policy π가 있는데 이 π는 각 state마다 어떤 action을 취해야 하는지 정한 것 입니다.
grid world에서는 총 9개의 state에서 action을 선택하는 것 입니다.
그림에서 보면 화살표가 나오는데 그 state에서는 화살표 방향으로 action을 취하겠다는 것 입니다. policy가 정해진 것 입니다. 즉, 각 하나의 그림은 하나의 policy를 표현한 것 입니다.
policy π : S -> A : 각 state마다 action을 주는 것
세 번째 그림의 경우 1,1에서 시작하면 policy에 따라 화살표 방향대로 움직이고 결국 +1을 얻으며 하나의 에피소드를 마치게 됩니다. 여기서의 reward는 4c+1로 c=-0.4로 했기에 total reward는 -0.6이 됩니다.
여기서는 Stochatic gird world이므로 화살표 방향대로 꼭 가지 않을 수 있습니다!
만약 1,1에서 east로 간다면? 여기서 다시 policy를 따라 가다가 3,2에서 north로 입력 받았지만 east로 가서 -1로 갈 수도 있는 것 입니다. 이렇게 되면 3c-1로 total reward -2.2를 얻게 됩니다.
이렇게 하나의 policy에 대해 여러 에피소드가 나올 수 있습니다.
그렇기에 각 policy에서 나오는 모든 episode의 기댓값(평균적인 보상)을 구하여 그 policy를 평가합니다.
이렇게 optimal policy π* 최적 정책을 찾는 것 입니다.
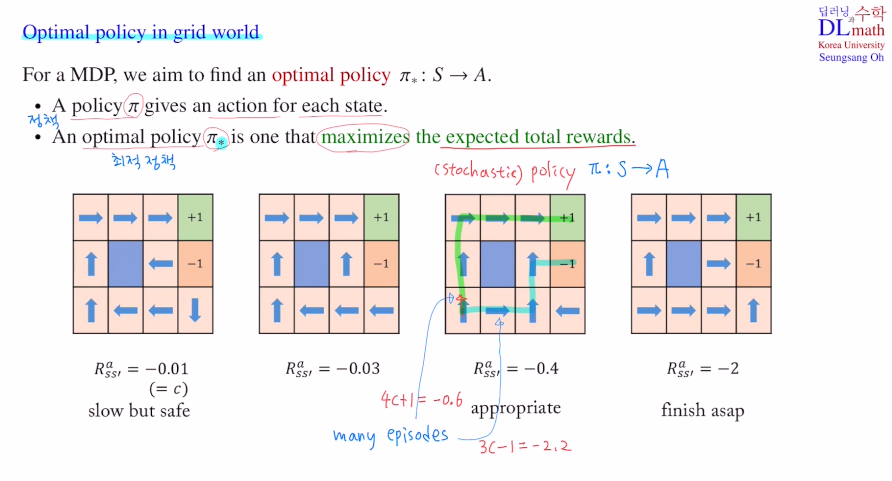
마지막 그림을 확인해보겠습니다. 여기서는 c=-2로 굉장히 큰 값을 가집니다. 그렇기에 한 번 움직일 때마다 치명적입니다. 그렇기에 최대한 적은 발걸음을 가는 것이 좋습니다. 또한 3,2에서 바로 오른쪽으로 가던 위로 갔다 오른쪽으로 가던 같은 값을 얻지만, 이 모델이 Stochastic이기에 위로 갔다고 하더라도 아래 혹은 왼쪽으로 이동할 확률도 있기에, 최대한 빨리 끝내버리는 것이 좋은 것 입니다. 따라서 3,2에서 오른쪽으로 가는 것이 best action이 됩니다.
첫 번째 그림을 보면 c값이 굉장히 작기에 최대한 안전하게가는 것이 좋습니다. 그렇기에 3,2에서 왼쪽으로 action을 취합니다. 그 이유는 위로 action을 취하면 10%확률로 오른쪽으로 가 -1을 얻고 게임이 끝날 수 있습니다. 그렇기에 차라리 왼쪽으로 방향을 두어 왼쪽을 선택하면 제자리에 있고, 10% 확률로 위로 올라가게 한 것 입니다. 절대 -1이 될 일이 없게 한 것 입니다.(4,1도 마찬가지로 south로 action이 정해져 있습니다.)
그렇기에 c값이 올라간 두 번째 그림의 경우는 화살표가 바뀌어 있는 것 입니다.
어떤 c값이 가장 적합할까요?
이는 optimal policy가 가장 이상적으로 보일 수 있는 세 번째 그림이 가장 좋을 것 입니다.
optimal policy는 DP이나 RL에서 찾고자 하는 목표가 됩니다.
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=S-7lXVpFci4&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=3
