이번 포스터에서는 Policy Gradient algorithm에 대해 알아보겠습니다!
이 알고리즘은 강화학습을 해결하는데 중요한 알고리즘입니다.
DQN에서는 state space가 너무 넓기에 해결하는 방법들을 이전 포스터에서 알아봤습니다. DQN은 action space가 한정적이기에 문제가 없었지만, action space가 커지는 경우도 생각해 보아야 합니다.
Policy Gradient algorithm에서는 conti action space를 다룰 수 있게 됩니다.
DQN에서는 Q-network를 통해 (s,a)에 대한 Q값을 approximate했습니다.
policy를 정할 때 highest q value를 갖는 action을 선택했습니다.
하지만 policy gradient algorithm은 policy를 neural network로 직접 학습합니다.
policy는 각 state에서 action에 대한 확률분포입니다.
이 policy를 신경망으로 학습하기에 이 확률분포를 parametric이라고 할 수 있습니다.
즉, parametric prob distribution이 되는 것 입니다.
input은 present state이 되고 output의 경우 DQN은 각 action에 대한 Q value였다면, 여기서는 action값을 stochastic하게 출력합니다. 즉, policy를 출력하는 것 입니다.
따라서 Q value ft을 학습하는 것과 달리, 이제는 policy를 output으로 출력하기에 무리가 없습니다.
예를 들어 로봇에서의 conti한 action space에 적용할 수 있는 것 입니다.
action space가 커도 action variable을 출력하기에 관절1,2,3,4에 대해 각도를 출력하여 (v1,v2,v3,v4) = (3,-2,1,-1)을 출력하게 됩니다.
네트워크를 학습할 때, 즉 Θ를 학습할 때, Q value ft을 approximate합니다. loss ft에서 둘 차이를 minimize시키는 것 입니다.
하지만 policy gradient는 total reward를 크게하는 방향으로 학습합니다.
또한 PG에서 output을 평균, 분산을 출력하면 이를 통해 가우시안 분포를 만들 수 있고 여기서 샘플링을 진행해도 되는 것 입니다! 이렇게 stochastic하게 할 수 있습니다.
action space가 작은 경우는 output을 action으로 둘 수도 있습니다. 마지막에 softmax를 통해 가장 좋은 action을 출력하는 것 입니다.
이제는 state를 통해 action을 얻는 것 입니다.
이렇게 반복하며 하나의 에피소드:Trajectory:τ 를 얻을 수 있습니다.
여기서의 total reward를 r(τ)라고 합니다.
그리고 이 r(τ)를 policy에 대한 expectation을 취한 값 EπΘ[r(τ)] 을 maximize하는 방향으로 학습을 진행하게 됩니다.
이 기댓값은 integral( p(τ;Θ)r(τ) )dτ 로 바꿀 수 있습니다.
여기서 p(τ;Θ)=πΘ(τ) 는 주어진 policy에서 τ가 나올 확률을 나타내는 것 입니다.
이것은 τ의 pdf가 됩니다.

이 목적함수를 maximize하는 방향으로 업데이트를 진행해갑니다.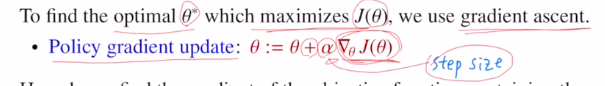
++ 여기서는 Experience replay를 사용하지 않습니다.
Experience replay를 사용했던 이유는 temporal correlation 때문이었습니다.
앞의 한 단계만 보며 진행을 하기에 로봇이 넘어지는 상황까지는 좋은 것이라고 생각하고 학습함을 지적하며 replay buffer이 나온 것 이었습니다. 하지만 여기서는 total reward를 사용하기에 모두 고려하기에 딱히 문제가 되지 않아 사용하지 않습니다.
Q. 추가적으로 우리는 gradient를 계산해야 하는데 expectation에 대한 gradient를 어떻게 계산할까요?
바로 Policy Gradient Thm을 적용합니다.
total reward의 expectation의 gradient를 바로 아래오 같이 표현하는 것 입니다!
policy에 log를 취한 후 gradient를 계산한 후 sum을 계산하고, 이것을 total reward와 곱한 것 입니다. 이것에 expectation을 최종적으로 취한 것 입니다. 이렇게 되면 expectation이 밖으로 나와 gradient를 계산하는데 문제가 없어집니다.
우선 expectation이기에 적분으로 변경해주고 gradient를 안으로 넣습니다.
그 후 식을 π(τ)/π(τ)=1 을 곱함으로 식을 변형하고 log로 표현해줍니다.
그리고 다시 expectation형태로 바꾸어줍니다.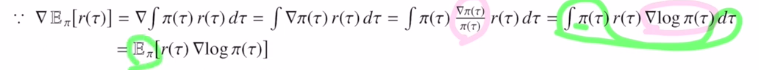
이제 안에 있는 식을 분해해보겠습니다.
Markov property를 만족함을 생각하며 확률을 간단히 표현해줍니다.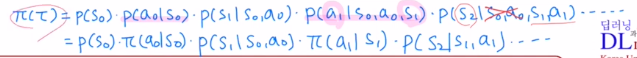
이 식을 log를 취했기에 sum으로 표현이 가능한데, transition prob는 gradient를 취하면 다 없어집니다.
이전에는 expectation을 계산하기 위해 p(τ;Θ)를 무조건 알아야했지만 사실 p(τ;Θ)를 전체를 아는 것은 거의 불가능합니다.(또한 transition prob p(st+1|st,at)를 알아야 계산이 가능합니다. 하지만 model free이기에 모릅니다.)
이제는 간편하게 계산이 가능합니다. 또한 expectation 계산은 미니배치를 통해 샘플링을 통한 approximation입니다.
expectation 계산은 미니배치 개수만큼 trajectory의 샘플을 찾은 후에 평균을 가지고 계산을 합니다. trajectory를 충분히 많이 찾으면 정확한 expectation을 찾아가는 방식입니다. unbiased approximation입니다.
이렇게 expectation을 샘플링을 통해 계산하는 방법을 Markov Chain Monte Carlo (MCMC) sampling 이라고 합니다.
Reinforce에서 이제는 expectation을 취하는 것 대신 M개의 샘플의 평균을 구한 것을 사용합니다.
total reward를 maximize하는 방향으로 학습합니다. trajectory의 total reward를 더 좋은 방법으로 대체할 수 있습니다. total reward는 policy와 아무 관계가 없습니다. 하지만 gradient를 계산하는 값마다 total reward를 곱하기에 전체 양에 영향을 미칩니다. total reward는 trajectory를 계속 갈 때 마다 randomness가 계속 발생하기에 variance가 굉장히 큽니다.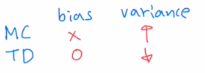
그나마 variance를 줄이는 방법이 discounted return Gt를 사용하는 것이었습니다.
뒤로 갈 수록 return값이 줄어 variance를 줄입니다.
원래 강화학습의 방향은 이미 지난 reward는 고려하지 않았습니다. 하지만 total reward를 사용하면 모든 reward를 고려하는 것 이기에 이론적으로 증명할 때는 total reward를 사용하였지만, 실제 적용할 때는 total reward 대신 discounted return을 사용합니다!
이렇게 이제는 total reward r(τ)대신 discounted return Gt를 사용하게 됩니다.
Gt는 이제 time step에 영향을 받기에 gradient 안으로 들어가게 되고, 이것이 REINFORCE가 됩니다!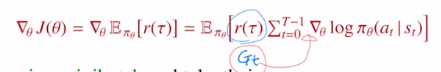
policy gradient가 최적으로 가는 방향이 됩니다.
return값은 얼마나 많이 가야 하는가가 됩니다.
다음 포스터에서는 policy gradient algorithm의 초기 모델인 REINFORCE에 대해 알아보겠습니다!
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=QoHWaruzGZ4
