이번 포스터에서는 TRPO의 Minorization-Maximization algorithm을 통해 DDPG에서 어려움을 겪었던 monotonic improvement를 어떻게 해결할지 알아보겠습니다!
1) old policy의 에타값을 사용해 추가적인 부분만 계산합니다.
state visitation frequency를 계산하는 것이 어렵기에 이 부분을 old policy로 바꾸어줍니다.
2) local approximation으로 Lπold(π)로 바꿔줍니다.
첫 번째 특징은 old policy에 대해서 에타값과 L값이 같습니다.
두 번째 특징은 old policy부분에서 gradient 값이 같습니다.
따라서 old policy근처에서는 L과 에타가 improve하는 것은 비슷합니다.
하지만 얼마나 큰 step으로 가도 improve되는 지에 대해서는 보장하지 않습니다.
3) 이를 해결하기 위해 conservative policy iteratoin update를 사용합니다.
original object ft에 approximate가 있는데 이것을 π'이라고 했을 때 π'를 바로 사용하는 것 아닙니다. 기존의 old policy보다 big step으로 이루어져 있다면 성능이 떨어질 수도 있습니다. 따라서 알파값을 이용해서 new policy 방향으로 조금만 움직이게 됩니다.
이렇게 정의하면 목적함수인 에타파이의 lower bound를 수학적으로 정의할 수 있게 됩니다.
(물론 lower bound가 improve한다고 해서 에타파이도 improve된다는 보장은 없지만 lower bound를 이용해서 많은 것들을 할 수 있게 됩니다.)
(입실론을 보면, 주어진 state에서 ad ft의 expectation을 구하는 것인데, new policy로 계산합니다. 그 후 모든 state에 대해서 maximum을 구합니다. mixture policy를 활용하기에는 어렵기에 4)에서 해결방안을 말합니다.)
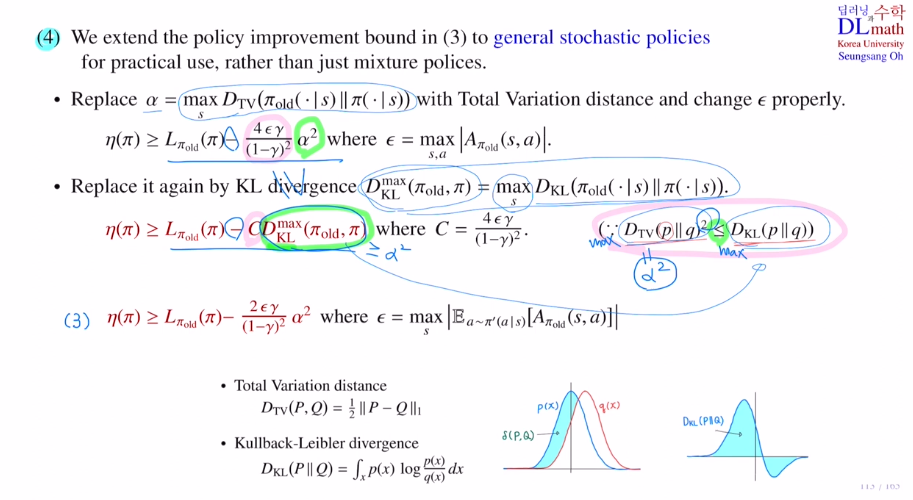
4) 세 번째에서 mixture policy를 이용한 policy improvement bound가 있었습니다. 이것은 practical하게 다루기 어려웠습니다. 그래서 일반적인 stochastic policy로 바꾸려고 합니다.
DTV(total varaince distance), DKL(KL-divergence)
이 둘은 확률 분포 사이의 거리를 재는 개념입니다.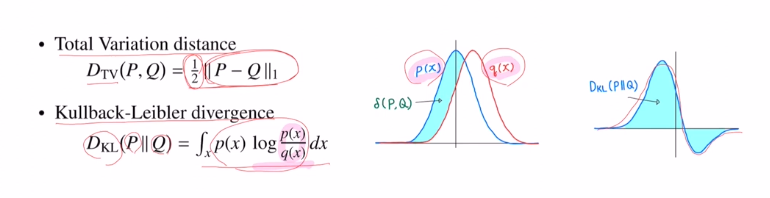
3에서는 알파를 하이퍼파라미터로 얼마나 나갈지를 정했는데, 여기서는 알파값을 정해주겠습니다.
old policy와 new policy의 tital variance distance를 찾습니다. 그 다음 모든 state에서의 maximum값을 알파로 잡습니다.
그리고 입실론값을 3과 달리 old policy에 대한 모든 (s,a)pair에서의 ad ft값의 maximum값을 입실론으로 잡습니다. 이런식으로 mixture policy를 사용하지 않아 단순화 시켰습니다.
또한 딥러닝에서 DTV보다 DKL이 다루기 쉽기에 KL-div에 관해서 lower bound를 변경해줍니다.
5) Minorization-Maximization algorithm : MM algorithm
위에서 구한 lower bound를 surrogate objective ft으로 사용합니다.
surrogate objective ft을 사용해서 MM algorithm을 하게 되면, 이 방법으로 update하게 된다면 이 policy는 monotomically improvement가 보장되는 것 입니다!
MM algorithm을 설명해보겠습니다.
이 알고리즘은 iterative method입니다.
아래의 세 단계를 반복하며 업데이트를 진행합니다.
1) surrogate objective ft을 찾는 것 입니다
surrogate objective ft은 아래 세 가지를 만족하는 ft입니다.
① 에타는 original obejective ft이고, Mi는 surrogate objective ft입니다.
surrogate objective ft은 그림에서 보는 바와 같이 current policy πi에서 둘이 같은 값을 가져야 합니다. 또한 항상 에타가 크거나 같아야 합니다.
② Mi는 에타의 lower bound입니다.
이 두 조건을 만족하고 둘 다 diff라면 current policy에서는 기울기값이 같게 됩니다.
따라서 MM에서 Minorization은 Mi가 에타의 lower bound라는 의미입니다.
③ original obejective ft 에타를 구하기 어렵기에 lower bound를 사용하는 것 이기에 Mi는 훨씬 optimize하기 쉬운 함수를 사용합니다. 여기서는 quadratic equation을 사용합니다.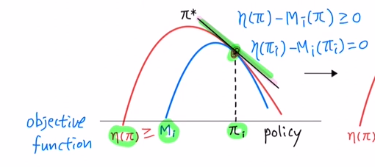
2) surrogate objective ft의 optimal pt를 찾는 것 입니다.
그리고 이것을 next policy로 사용합니다.
η(πi) = Mi(πi) <= Mi(πi+1) <= η(πi+1)
next policy에 대해 object ft값이 η(πi) <= η(πi+1) 를 통해 증가함을 확인할 수 있습니다.
그렇기에 monotonic improvement를 보장할 수 있습니다!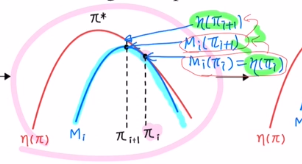
3) 이제 또 다른 surrogate objective ft Mi+1 을 찾은 뒤에 반복하는 것 입니다.
이것이 MM알고리즘 입니다. 이를 통해 monotonic improvement를 보장하며, local or global optimal에 도달하게 됩니다.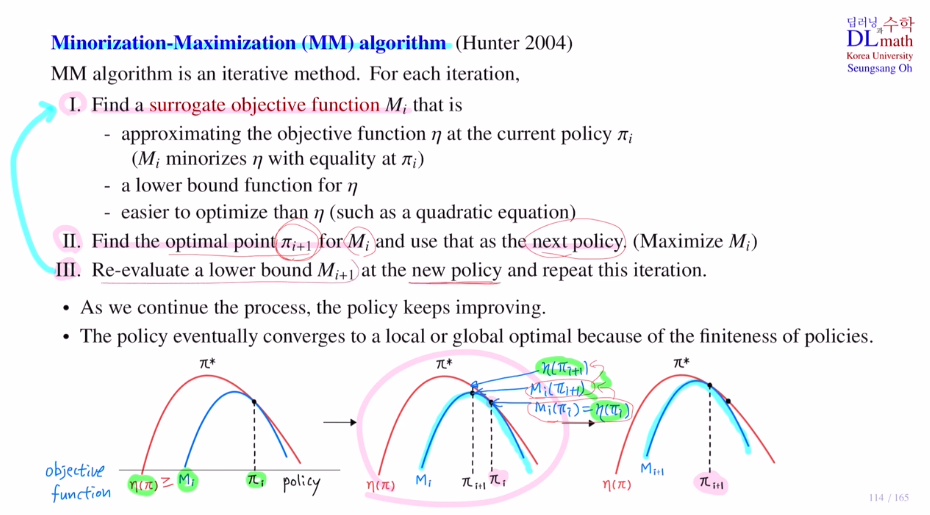
이제 MM알고리즘을 모델에 적용해 보겠습니다.
surrogate objective ft Mi는 아래와 같습니다.
이렇게 구성한 식은 첫,두 번째 조건을 만족합니다.
또한 monotonic improvement를 보장할 수 있습니다.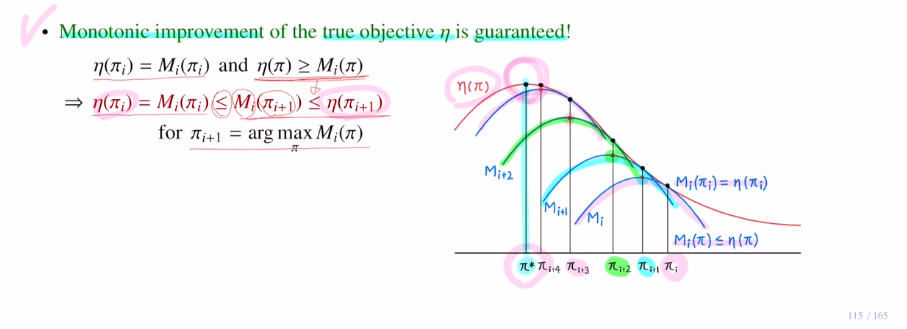
이제 5단계를 들어가겠습니다. 여기는 앞에서 정의한 이론적인 논리들을 practical하게 바꾸는 것 입니다.
5) Minorization-Maximization algorithm
policy를 나타내기 위해서는 π(a|s)를, policy를 나타내는 파라미터를 표현하기 위해서는 Θ를 사용합니다.
MM알고리즘을 하기 위해서는 상당히 많은 계산이 필요합니다. 계산해서 나온 값은 next policy가 됩니다. 이 next policy를 old policy로 정의해서 surrogate objective를 maximize하는 세타를 또 찾아서 그것이 next policy가 되는 것 입니다. 이를 계속 반복해야 하기에 많은 계산량이 필요한 것 입니다.
만약 discoutn factor가 1에 가까워진다면, C값은 커지게 되는 것이고, 그렇게 되면 식을 maximize하기 위해 KL-div값을 작게 하기 위해 Θold, Θ 사이를 작게 할 수 밖에 없습니다. 그렇게 되면 optimize가 굉장히 천천히 진행됩니다.
6) Trust region constraint
surrogate objective ft을 maximize하는 것이 목표였습니다. 이 식을 KL penalized objective라고도 합니다. 이 식에서 KL-div term만을 KL constraint objective라고 합니다.
이 KL constraint objective <= δ 를 만족할 때, L old를 maximize하는 것으로 변형했습니다. 계산이 무한이 주어진다면 두 식을 일치합니다.(Lagrangian duality)
C가 커지면 step size를 작게 해야 했습니다. large step size를 robust하게 사용할 수 있는 방법이 KL constraint 를 사용하는 것 입니다.
따라서 이 constraint를 Trust region이라고 합니다.
하지만! 모든 state에 대해서 만족시켜야 하기에 이것은 쉽지 않습니다.
7) 따라서 이 부분을 해결하고자 Heuristic approximation을 사용합니다.
여기서는 constraint 부분을 maximize 대신 expectation을 취합니다.
Monte carlo 시뮬레이션을 쓰기에 샘플로 대체할 수 있기에 expectation을 사용하게 됩니다.
8) Monte Carlo simulation
이제는 expectation을 직접 계산하는 것이 아닌 샘플을 통해 계산합니다.
single path method, vine method 둘을 논문에서는 사용합니다.
앞에서는 L old였지만 이제는 여기서 에타를 뺍니다. 에타는 상수이기에 빼도 무방합니다.
우선 frequency에 1-ρ 를 곱해주면 확률이 되었습니다. 이를 통해 식을 변경해줍니다.
그리고 Ad ft을 Q ft으로 바꿔줍니다. (state value ft은 policy와 관계가 없기에 policy입장에서는 상수입니다. 그렇기에 maximum 값 자체는 바뀌어도 maximize하는 세타값은 바뀌지 않습니다.)
new policy를 사용하면 Monte carlo simulation을 사용할 수 없습니다. 왜냐하면 new policy에 대한 샘플이 없기에. 그렇기에 old policy로 바꿔줍니다. 이 방법이 Importance sampling입니다. (다루기 어려운 확률분포를 변경하여 weight를 곱하고 샘플링을 해줍니다.)
old policy에 대한 state visitation frequency에 대한 expectation으로 바뀌었고, old policy를 따르는 action에 대한 expectation으로 바뀌었고 그럼과 동시에 importance weight가 곱해졌습니다. 그리고 Ad ft은 Q ft으로 바꾸었습니다. 뒤의 KL constraint term은 동일합니다.
직접 적용할 때는 current policy를 가지고 데이터를 생성할 텐데 평균을 가지고 expectation을 대체합니다.(Monte Carlo simulation) 그리고 Q ft에 대해서는 Q net를 만들어줍니다.
9) Practical algorithm solving TRPO
policy update를 one iteration이라고 합니다.
set of state-action pairs는 trajectories on pi(old)입니다.
그리고 이 trajectories(샘플들)을 가지고 Q net을 업데이트 합니다.
expectation 대신 Monte carlo로 샘플들의 평균을 이용하여 object와 constraint를 계산합니다.
이제 policy를 업데이트하여 new policy를 찾는데 이 때 사용하는 방법이 Natural Policy Gradient를 사용합니다.(2nd order optimization) 여기서는 Conjugate gradient를 사용합니다. 맨 마지막에는 backtracking으로 Line search도 사용합니다.
고려대학교 오승상 교수님 강화학습 : https://www.youtube.com/watch?v=ojgn1xBWfGo&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=28
