TRPO에서는 Minorization-Maximization algorithm과 Trust region을 사용했습니다.
Trust region을 사용하면 object ft인 expected return의 monotonic improvement가 보장되었고, 그렇기에 step size를 크게 걱정하지 않아도 되었습니다.
surrogate ojective를 maximize함을 반복하면 original optimal policy에 도착합니다.
하지만 여기서 감마가 1로 감에 따른 C값의 증가로 surrogate ojective를 maximize하기 위해 세타old와 세타의 거리가 짧아져 조금만 움직이게 됩니다.
따라서 constraint term을 따로 떼었습니다. 근거는 Lagrangian duality입니다.
최종적으로 바꾸면 expectation을 모두 old policy로 합니다.(old policy=current policy)
따라서 current policy에서 샘플링을 통해 Monte Carlo simulation을 사용해서 expectation대신 sample average를 사용하게 됩니다. 그리고 Q net을 가지고 있습니다.
9) Practical algorithm solving TRPO
policy update를 one iteration이라고 합니다.
set of state-action pairs는 trajectories on pi(old)입니다.
그리고 이 trajectories(샘플들)을 가지고 Q net을 업데이트 합니다.
expectation 대신 Monte carlo로 샘플들의 평균을 이용하여 object와 constraint를 계산합니다.
이제 policy를 업데이트하여 new policy를 찾는데 이 때 사용하는 방법이 Natural Policy Gradient를 사용합니다.(2nd order optimization) 여기서는 Conjugate gradient를 사용합니다. 맨 마지막에는 backtracking으로 Line search도 사용합니다.
이제부터 Natural Policy Gradient: NPG에 대해 알아보겠습니다.
NPG는 테일러급수를 통해 approximation을 하게 됩니다.
목적함수가 있으면 이것은 테일러급수의 1st order linear term으로 approximation을 하게 됩니다.
lieanr term이 있고, gradient가 있습니다. KL-div인 constraint는 2nd order term으로 approximation합니다.(여기서는 두 번 미분한 헤시안을 사용합니다. 이를 fisher information matrix하고 합니다.) 각 샘플에 대한 값을 계산한 후에 N개 샘플에 대한 평균을 fisher information matrix로 합니다.
surrogate object ft을 아래와 같이 변경합니다.
이제 gradient를 구하는데 여기서는 Natural Gradient를 사용합니다.
기존 Gradient가 있을 때 앞에 H-1를 곱해주는 것 입니다. 이를 통해 더 효율적으로 갈 수 있습니다.
이계도함수인 헤시안은 curvature로 얼마나 휘어있는지 입니다.
이렇게 헤시안을 통해 사용한 것은 휘어짐 정도를 따라 방향을 잘 수정해 줄 수 있습니다.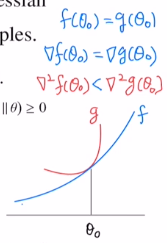

Natural Gradient을 사용하기 위해서는 헤시안 이 있어야 하는데 계산량이 훨씬 많이 들기에 잘 사용하지 않았습니다.
여기서는 constraint term 때문에 헤시안을 계산해야 하기에 이것을 사용하여 Natural Gradient방법을 도입한 것 입니다!
이제 step size를 잘 정해서 업데이트를 합니다.
Θ = Θold + βH^-1g
이 식에 적용하면 위와 같이 나오고, 만족하기 위해서는 델타와 같으면 됩니다. 이것을 β를 정리하여 아래와 같이 바꿔줍니다. 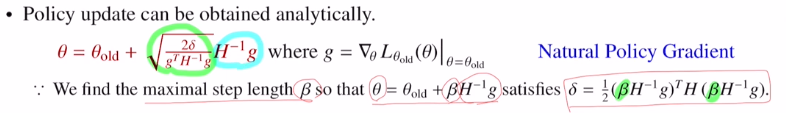
다시 정리하자면 NPG는 2nd order gradient입니다.
그렇기에 더 빨리 converge합니다. 하지만 gradient는 dim이 n이라면 헤시안은 nxn이 됩니다. 많은 계산량이 요구되는데 이 헤시안의 inverse까지 구해야 하니 굉장히 어렵습니다.
따라서 H inverse를 구하는 것 대신 H(-1)g를 계산합니다.
x = H(-1)g 라고 할 때, x를 구한다는 말과 Hx = g의 해를 구한다는 말과 동일합니다.
또한 이것과 min x f(x) = 1/2xTHx-gx 와 동일합니다. 따라서 x를 계산하기 위해 f를 minimize하는 x를 찾는 문제로 바꾼 것 입니다.
또 하나는 H의 특징은 positive-definite matrix라는 특징이 있습니다. 그렇기에 기존의 gradient descent가 아닌 conjugate gradient descent를 통해 훨씬 더 작은 iteration에서 방법을 구할 수 있습니다.
(물론 conjugate gradient descent도 복잡합니다.)
마지막으로 Line search라는 테크닉입니다.
step size가 정말 object term을 improve시키는지, KL-constraint term을 만족을 하는지를 확인을 하는 작업을 해야합니다.
maximum value로 얻은 베타를 통해 실제로 object term과 KL-constraint term에 적용시켜 줍니다. 만족으로 하면 적합한 것 입니다. 만약 더 큰 값이 나왔다고 하면 베타값을 줄여야 하는 것 입니다. 따라서 0<알파<1 를 통해 알파를 곱함으로 베타값을 줄이며 만족하는지 확인합니다.
TRPO의 수도코드를 확인하겠습니다.
policy parameter 세타를 초기화해줍니다.
old policy에서 샘플을 얻어 냅니다. (여러 trajectories)
목적함수를 계산하기 위해 우선 Ad ft을 estimate하는 네트워크를 통해 주어진 샘플들을 가지고 값을 estimate합니다.
그 다음 샘플들을 가지고 policy gradient를 계산합니다. (using advantage estimate)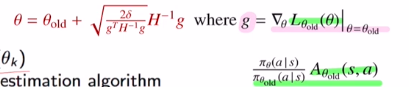
이제는 Natural Gradient를 계산해야 하는데 Hx=g의 솔루션을 구하게 됩니다.
그래서 헤시안을 계산해서 conjugate gradient를 통해 x를 찾아줍니다.
그 x값을 통해 Natural gradient를 estimate해줍니다.
그 다음 Natural gradient에 step size 베타값을 곱하여 업데이트를 시켜줍니다.
하지만 바로 업데이트 하지 않고 Line search로 알파값을 곱하여 그 다음 업데이트를 시킵니다. 이를 반복적으로 적용해서 object가 improve되고 KL-constraint term이 만족되면 그 때 멈춰서 최종 policy를 new policy로 업데이트 합니다!
TRPO는 헤시안을 계산해야 하기에 많은 계산량을 요구합니다.
따라서 deep CNN과 같이 파라미터 수가 많은 경우는 TRPO를 practical하게 사용할 수 없습니다.
따라서 이 문제를 PPO를 통해 2nd order optimization을 1st order optimization으로 바꿔줍니다.
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=Q3_mJFKiEwc&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=29
