이전 포스터까지에서는 TRPO를 알아보았다면, 이번 포스터에서는 Proximal Policy optimization: PPO을 알아보겠습니다!
TRPO에서는 monotonic improvement를 보장하기 위해 surrogate obeject ft을 MM알고리즘을 통해 사용했습니다. 이것을 maximize하는 policy를 찾는 것 이었는데, 여기서는 trust region 역할을 하는 KL constraint term 조건이 하나 따라 붙었습니다. 이 term을 통해 policy가 급격하게 바뀌는 문제를 방지하며 TRPO는 좋은 성능을 갖고 있습니다.
하지만 이 constraint term의 계산 복잡성으로 문제가 있었습니다. implement and complicated 여러 단계로 approximation, objective ft을 tayler series로 approximate할 때 앞 부분은 1계 도함수로 approximate하지만 뒷 부분은 2계 도함수로 approximate를 해야 하기에 FIM H 헤시안을 계산해야 했습니다.
하지만 constraint term은 trust region으로 policy ratio가 너무 커지거나 너무 작아지는 것을 막아주기에 필요한 부분입니다. 따라서 PPO에서는 constraint term을 없애는 대신 policy ratio에 직접 제한을 가합니다. 이 방법을 clipping이라고 합니다.
만약 old policy와 new policy가 비슷하면 policy ratio는 1에 가까워질 것입니다. 만약 다르다면 1보다 확 커지거나 작아지게 됩니다. 그렇기에 이 policy ratio를 1-ε, 1+ε 사이로 올 수 있게 하는 것 입니다. 만약 ratio가 1.3인데 ε=0.2로 0.8, 1.2라면 ratio를 1.2로 잡는 것 입니다. 이렇게 함으로 KL-div 에 델타를 통해 제한을 두는 효과와 비슷한 작용을 하게 됩니다. 이렇게 constraint term을 없앨 수 있는 것 입니다. 이제는 FIM를 사용하지 않고 1st order stochastic gradient만 계산하면 되어 계산량이 많이 줄게 됩니다.
이것을 Clipped surrogate obkective ft이라고 합니다.
여기서는 minimum이 추가되어 있습니다. 그 이유는 단순히 maximize하는 것 뿐 아니라 이 식이 원래 objective ft의 lower bound가 되어야 하기 때문입니다! 그래야 surrogate objective ft이 되어 MM algorithm을 사용할 수 있게 됩니다.
이 식은 TRPO의 lowerbound 가 됩니다.
surrogate objective ft을 쓸 때, MM algorithm을 사용하기 위해 조건이 있었습니다.
surrogate objective ft은 원래 objective ft의 lowerbound 가 되면서 old policy에서 같은 값을 가져야 했습니다. 이 두가지 조건을 만족해야 MM알고리즘을 사용할 수 있습니다.
lower bound, old policy 조건도 만족하여 CLIP또한 MM알고리즘을 사용할 수 있게 됩니다.
이를 통해 계산량을 줄이고 기존의 목표인 monotonic improvement를 보장할 수 있습니다.
이러한 장점으로 Open AI에서는 DRL의 대표적인 알고리즘으로 PPO를 사용합니다.
이번에는 Ad ft앞에 붙는 ratio, clip 중 minimum을 취함으로 나오는 효과에 대해 알아보겠습니다.
Ad ft은 아래와 같으며 V(s)가 모든 action에 대한 Q ft의 expectation이기에 Ad ft값이 양수라는 것은 좋은 action이라는 것이기에 이 action이 나올 확률을 높여주어야 합니다.
즉, action을 encourage시키기 위해 ratio값을 올려주어야 합니다.
이렇게 되면 ratio값이 1보다 커지게 됩니다. 이 값이 너무 커지면 문제가 되었습니다. 이 때 clipping을 통해 (0.8, 1.2) 사이에 들어오게 만들어줍니다. 반대로 Ad<0라면 줄여주어야 하는데 또 너무 작아져버리면 변화량이 너무 크기에 이 또한 사이에 들어오게 합니다.
만약 ratio가 1.4로 나온다면 목적함수에 minimum 조건이 있기에 1.2로 변경되어 계산을 하게 됩니다. 하지만 만약 Ad ft값이 양수가 나왔는데 ratio값이 0.7이라면 clipping으로 인해 0.8로 바뀌기에 clipping을 하지 않은 값이 선택됩니다. (clipping효과가 사라집니다)
굳이 clipping효과를 없애는 이유는 TRPO보다 CLIP이 크게 되어 조건을 만족하지 않게 됩니다.
PPO를 실제로 implementation하는 부분을 살펴보겠습니다.
CLIP objective ft에 추가적으로 두 부분이 붙었습니다.
VF는 value estimation의 error term입니다. Ad ft을 estimate하기 위해서 Q,V ft을 estimate할 네트워크 두 개가 필요합니다. 이 네트워크의 구조는 당연히 같지만, 파라미터 또한 일정 부분 share할 수 있습니다. 이렇게 share을 하게 되면 안정적으로 바꿔주기 위해 error term을 추가해 주는 것 입니다.
두 번째 term은 entropy(무질서) bonus라고 합니다.
이 부분은 exploration을 주기 위해 noise를 주는 것 입니다.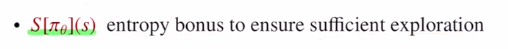
이렇게 weight share을 할 때 안정적으로 만들기 위해 error term을 빼주고, exploration을 주기 위해 entropy bonus를 첨가해주어 PPO의 목적함수를 완성합니다. (하이퍼 파리미터 c1,2를 통해 조절해줍니다.)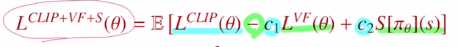
마지막으로 DRL 알고리즘들을 비교해보겠습니다.
앞의 두 개는 RL알고리즘이고(Q table - 모든 (s,a)에 대한 Q값을 저장), 나머지는 DRL 알고리즘(Q network)입니다.
A3C이후부터는 network로 policy 자체를 구현하여 conti policy space에서도 가능하게 됩니다.
TRPO을 통해 monotomic improvement를 보장하고, 계산량 또한 효율적으로 만든 것이 PPO입니다.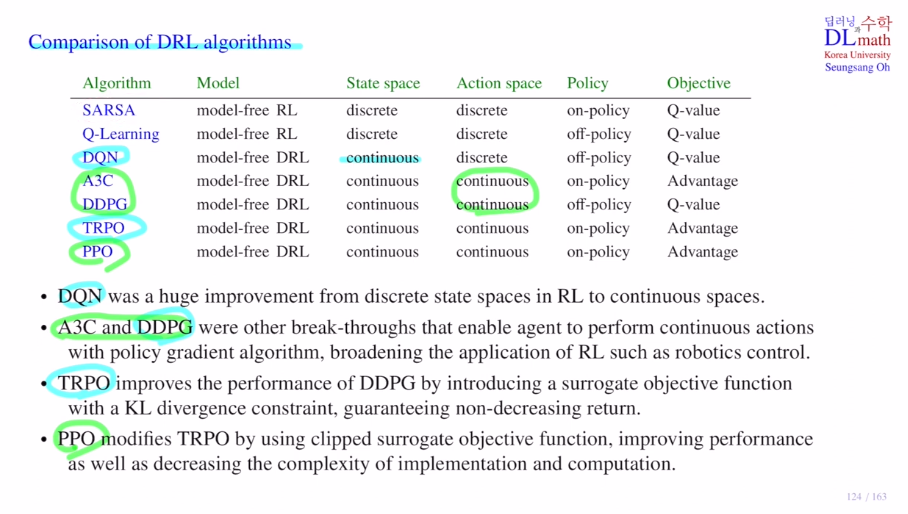
고려대학교 오승상 교수님 강화학습 : https://www.youtube.com/watch?v=5fHbx33bqBc&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=30
