이번 포스터는 reward, return, policy등에 대해 알아보겠습니다.
우선 reward에 대해 살펴보겠습니다.
Reward는 Rt로 표현하며, agent가 한 행동이 얼마나 좋은지 안 좋은지 feedback하는 scalar값을 말합니다.
agent는 한 policy에서 모든 epicodes에 대해 평균 total reward를 극대화하는 것이 목표입니다.
maximize cummulative sum of reward : total reward : Gt
한 에피소드에서 얻은 reward를 Gt라고 하겠습니다.
강화학습의 핵심은 Reward Hypothesis를 기반으로 하고 있습니다.
강화학습의 모든 목표는 각 에피소드에서 나온 cummulative sum of reward 값들의 평균값을 maximize하는 쪽으로 agent는 학습을 진행하는 것 입니다.
바둑의 경우는 매번 수를 둘 때마다 보상을 주는 것이 아닌 마지막에 끝나고 한번 보상을 줍니다. 탁구게임의 경우는 매 번 득점을 할 때 마다 보상을 주게 됩니다.
이번에는 expected reward라는 개념에 대해 알아보겠습니다.
먼저 state transition probability에 대해 말해보겠습니다.
state transition probability는 Markov process와 Markov Decision process에서 달랐습니다.
먼저 Markov process에서 state transition probability는 P(s'|s) 현재 state에서 다음 state로 넘어가는 확률을 의미했고,
Markov Decision process에서 state transition probability는 action이 포함되어 있어 P(s'|s,a)로 현재 state에서 action이 주어졌을 때 다음 state로 넘어가는 확률을 의미했습니다.
여기서 확인해 볼 점은 아래와 같이 s와a에 대해 s'으로 가는 확률과 s와a에 대해 s'으로 가고 reward를 r'으로 받을 확률이 같을 때가 있습니다.
P(s'|s,a) = 0.4 = P(s',r'|s,a)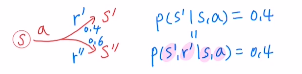
하지만 모델이 훨씬 복잡하면 reward를 주는 방식이 달라져 같은 state로 가지만 reward를 다르게 받을 수도 있는 것 입니다. 아래와 같이 s'으로 갈 때 reward를 주는 방식이 2가지가 있다면(50%확률로 받는다.) state transition probability를 더욱 자세히 만들 필요가 있습니다.
P(s'|s,a) = 0.4 이지만 P(s',r'|s,a) = 0.4 0.5 = 0.2가 되고, P(s',r''|s,a) = 0.4 0.5 = 0.2 이기 때문에 둘을 합하면 0.4가 됩니다.
이렇게 더 세분화 된 것을 dynamic이라고 부릅니다.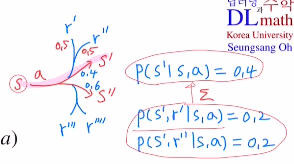
만약 이 dynamic을 다 안다고 가정할 때, state transition probability나 expected reward들을 계산해 보겠습니다.
먼저 state transition probability를 보면, 현재 state에서 action을 취하고 next state로 갈 확률은 reward를 세분화하여 그것들의 sum을 한 것과 같아집니다.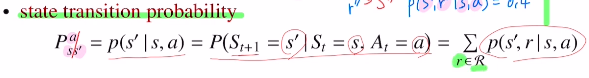
이번에는 expected reward for state-action pair을 알아보겠습니다.
reward의 종류는 Rs, Rsa, Rsas' 이 있다고 했습니다. 여기서는 Markov Decision process를 다루어 action이 포함되어 있기에 두 가지에 대해서만 하겠습니다.
Rsa는 현재 state에서 action을 취하면 받는 보상값으로, 만약 보상이 r하나만 있다면 Rsa=r이 될 것입니다. 하지만 아래와 같이 s에서 action을 취하면 0.4확률로 s'으로 가고, 0.6확률로 s''으로 간다면, 총 받는 기대 보상은 0.4 r' + 0.6 r''이 될 것 입니다. 이는 다시 표현해서 r' P(s',r'|s,a)(=0.4) + r'' P(s',r''|s,a)(=0.6) 이 됩니다. 따라서 아래와 같은 식이 구성됩니다.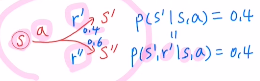
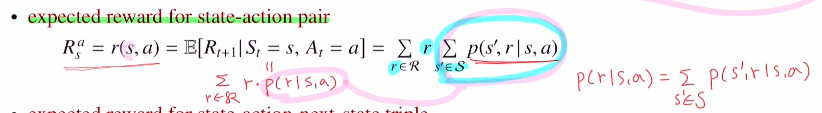
이번에는 expected reward for state-action-nextstate triple에 관한 것 입니다.
Rsas' 으로 sum(r p(r|s,a,s')) 입니다.
여기서 조건부확률을 변형시킵니다. p(r|s') = p(s',r)/p(s') 인데, 여기서 조건부를 모두 추가할 수 있습니다. 그러면 p(r|s,a,s') = p(s',r|s,a)/p(s'|s,a) 가 됩니다. 그렇기에 sum(r p(r|s,a,s')) = sum(r* p(s',r|s,a))/p(s'|s,a) 가 되는 것 입니다.
이 식들은 Bellman equation을 증명할 때 사용하게 됩니다.
이번에는 Return이라는 개념을 보겠습니다.
Return은 Gt라고 표현하며, 현재 time step t에서 이후에 얻어지는 total discounted reward를 Ruturn이라고 합니다.
Discount factor는 γ라고 표기하며, 감가율이라고 합니다. 이는 0~1값을 가져 뒤로 갈 수록 감마를 계속 곱하여 이후에 얻을 reward들의 값을 낮춰줍니다.
그 이유는 현재 얻는 reward는 명확하지만 갈 수록 Stochastic이기에 불명확해지기 때문입니다.
보통 멀리 있는 값이 필요없으면 γ값이 작아지고, 멀리 있는 값도 중요하면 γ값을 1에 가깝게 설정합니다. : myopic 0 <= γ <= 1 far sight
MDP에서는 이 discounted를 사용합니다.
그 이유는
1) 수학적으로 안전하고 편합니다.
만약 γ를 사용하지 않는다면 게임이 끝나지 않게 되면 계속 reward가 더해집니다. 이렇게 되면 infinite value를 갖기에 좋지 않습니다. 그렇기에 γ를 통해 finite하게 값을 조정할 수 있는 것 입니다.
2) 미래에 대한 불확실성을 반영할 수 있습니다.
time step이 지날 수록 reward의 가치가 줄어드는데 이러한 불확실성을 γ를 통해 reward값을 줄여 반영시킬 수 있습니다.
따라서 MDP에서 discounted를 사용하는 것 입니다.
하지만 만약 finite게임이라면 굳이 discounted를 하지 않는 경우도 있습니다.
이번에는 Policy에 대해서 알아보겠습니다.
강화학습의 최종 목표는 최적의 policy를 찾는 것 입니다.
이 Policy는 보통 stochastic policy를 사용합니다.
stochastic policy π는 각 state마다 action에 대한 확률분포를 의미합니다.
π(a|s) 는 주어진 s라는 state에서 action인 a가 될 확률을 의미합니다. 모든 state마다 이 값을 정해주는 것이 policy입니다.
만약 deterministic policy라면 π(s) = a가 됩니다. 여기서는 확률값이 아닌 acton이 policy 가 됩니다.
아래의 그림을 보면 s에서 시작하여 a1,a2,a3의 action 을 취하면, 거기서 부터 많은 에피소드들이 생깁니다. a1에 따른 return을 G1, a2에 따른 return을 G2, ㅁ3에 따른 return을 G3라고 하겠습니다.
이 세 가지의 각각 return의 평균이 E[G1]=7, E[G2]=10, E[G3]=1 이라고 하겠습니다. E[G2]이 가장 높게 나왔기에 a2를 선택하는 것이 가장 좋을 것 입니다. 그렇기에 a2로 가는 확률을 0.8, a1으로 갈 확률을 0.15, a3로 갈 확률을 0.05라고 설정할 수 있습니다.
=> 이를 stochastic policy라고 하며 π(a1|s)=0.15, π(a2|s)=0.8, π(a3|s)=0.05가 됩니다.
즉 policy π는 "Return 값을 maximize하기 위해 optimal action이 무엇인지를 말해주는 guide line"이 되는 것 입니다.
(여기서 이전 state는 절대 고려하지 않습니다.)
다음으로 known MDP (state transition probability를 알고있는 경우) 와 unknown MDP(state transition probability를 알고있지 않은 경우) 를 알아보겠습니다.
known MDP의 경우는 state transition probability를 모두 알고 있기에 Dynamic programming을 사용합니다. 모든 값들을 계산할 수 있기에 E가 가장 높은 action을 선택하면 되는 것입니다. 그렇기에 optimal한 policy π* 가 항상 존재합니다.
하지만 이제부터 알아볼 강화학습은 unknown MDP입니다.
따라서 state transition probability를 모르기에 샘플 데이터만을 가지고 한정적으로 알고 있기에 정확한 계산을 할 수 없습니다.
그렇기에 여기서 ε-greedy policy(stochastic policy)를 사용합니다.
예를 들어 아래와 같이 a1,a2만 알고 있을 때 a2가 best action이라면 policy를 정할 때 어떻게 할까요? a2로 가는 확률을 그냥 1로 해버리면 a3,4,5에서 더 좋은 경우가 있을 수도 있는 데 손실을 보게 됩니다.
이 경우 a2에 0.9로 두고, ε=0.1로 잡아 action의 개수만큼 쪼개어 a1,2,3,4,5에 나눠주는 것 입니다.
a1로 갈 확률 0.02 / a2로 갈 확률 0.92 / a3로 갈 확률 0.02 / a4로 갈 확률 0.02 / a5로 갈 확률 0.02
이렇게 함으로 가능성을 열어줍니다.
아래는 용어들을 정리한 것으로 참고하시면 좋을 것 같습니다.

고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=Mvzu5CwcUpw&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=4

