이번에는 Bellman Equation을 알아보겠습니다.
컴퓨터가 계산하기 위해 수학적으로 잘 정리한 것이 MDP입니다. 이 MDP를 해결하기 위해 가장 기초적인 개념이 value ft인데 이 value ft을 계산하기 위한 것이 Bellman Equation입니다.
우선 Value ft에 대해 알아보겠습니다.
이것은 가치함수로 각 state가 얼마나 좋은 지 평가하는 지침이 됩니다.
다시 말해 현재 state가 얼마나 많은 보상을 얻을 수 있는 지 를 나타내는 양입니다.
우선 1) State-value function을 알아보겠습니다.
policy를 따라 갈 때 많은 에피소드들이 나올 텐데 이 때 나오는 Retrun값들의 기댓값으로 정의됩니다.
vπ(s) = E[Gt|St=s] 현재 state에서부터 모든 에피소드에 대한 return 값들의 expectation
이것으로 현재 state가 좋은 지 좋지 않은지 평가하는 것 입니다.
두 번째는 2) (state) Action-value function입니다.
qπ(s,a) 로 표현하며, 현재 state에서 특정 action a를 실행했을 때 그 때 얻게 되는 retrun값들의 평균값 입니다. state value ft과 시작점이 다른 것입니다.
그렇기에 예를 들어 아래와 같이 각 action에 따른 평균 return값을 알고 있다면, 다음 action을 무엇으로 실행할지 policy를 수월하게 정할 수 있습니다. 하지만 state valu ft은 그렇지 않습니다.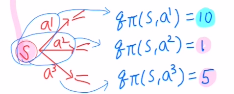
하지만 단점도 있습니다. (s,ai)들을 모두 계산해야 하기에 계산량이 훨씬 많아집니다.
참고로 앞으로 배우게 될 다이나믹 프로그래밍과 Reinforcement learning의 차이를 비교해보면 현재 여기 있는 expectation을 계산하는 방법의 차이가 있습니다.
DP에서는 Known MDP입니다. π(a|s)와 P(s'|s,a)로 직접 기댓값을 구할 수 있습니다.
이를 dynamic programming으로 계산합니다. 하지만 action-value ft에서는 (s,a) pair들을 모두 계산해야 하기에 계산량이 너무 많습니다. 그렇기에 state value ft에서만 dynamic programming이 쓰입니다.
반대로 강화학습은 model-free 로 unknown MDP입니다. 다시 말해 transitoin probability를 알지 못 하게 된 것 입니다. 즉, expectation을 정확하게 계산할 수 없기 때문에 추정치를 계산합니다. 이 방법이 Monte carlo가 됩니다. 따라서 샘플에 있는 것만 계산을 하기에 pair가 많아도 강화학습은 진행할 수 있는 것 입니다.
마지막으로 Advantage ft은 action value ft과 state value ft과의 차이 입니다.
Advantage ft Aπ(s,a) = qπ(s,a) - vπ(s,a)(:모든 action value ft의 기댓값) 입니다.
이것이 양의 값을 가지면 action a가 평균보다 좋다는 의미 입니다. 반대로 0보다 작으면 action a가 평균보다 기대되는 return이 적기에 bad action이 됩니다.
이번에는 강화학습에서 자주 언급되는 확률 이론 두 가지를 알아보겠습니다.
첫 번째는 1) Law of tatal probability 입니다.
이는 전체 확률의 법칙으로 B가 가지고 있는 조건 두 가지로 P(A)를 아래와 같이 나타낼 수 있습니다. 그리고 이를 통해 아래와 같이 구성합니다.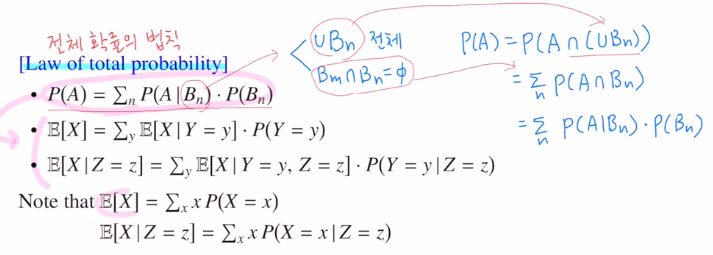
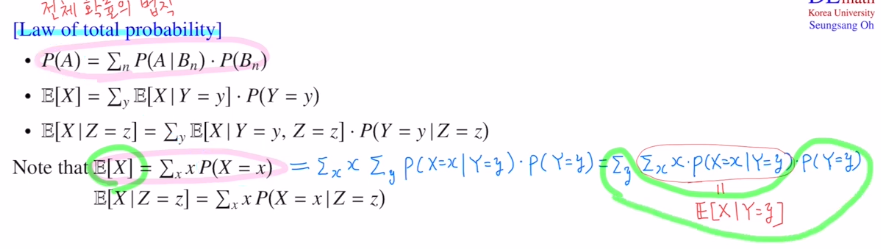
두 번째는 2) Law of large numbers 입니다.
큰 수의 법칙 입니다. 확률변수의 기댓값을 계산해야 하는데, 실제 이것을 계산할 수 없기 때문에 iid(독립항등분포) random 샘플들을 이용해서 계산을 진행합니다. 여기서 랜덤 샘플들의 개수가 증가할 수록 전체 평균값에 근사한다는 것 입니다.
예를 들어 동전을 던질 때 H:1 T:0 이라고 할 때, 동전이 구부러져 있다고 가정하겠습니다. 여기서 H의 확률이 p라고 하면 T의 확률은 1-p가 될 것이기에 E[x]=1p+0(1-p)로 p가 됩니다. 하지만 p를 현재는 모릅니다. 그렇기에 이런 경우 계속 전져가며 trials를 통해 random sampling을 진행합니다. 이 랜덤 샘플 수가 많아질 수록 p에 근사해지는 것 이기에 p의 추정치를 구할 수 있고 이는 E[x]를 근사할 수 있다는 것 입니다. .
.
이제는 Bellman Equation에 대해 알아보겠습니다!
Bellman expectation Equation이 있고, Bellman optimality Equation가 있습니다. 이번 포스터는 Bellman expectation Equation에 대해서 다루겠습니다.
아래는 State-value function에 대한 Bellman expectation Equation과 Action-value function에 대한 Bellman expectation Equation이 있습니다.
State-value function부터 보면 전체 return값들을 알아야 합니다. 그렇기에 에피소드가 끝나기 전까지는 값을 알 수가 없습니다.
그렇기에 이 식을 law of tatal probability로 변형해보겠습니다.
이번에는 return의 정의를 통해 Gt를 Rt+1 + γGt+1로 변경했습니다.
이번에도 law of tatal probability로 변형한 것인데 이번에는 action이 아니라, next state s'과 r에 대해 적용한 것 입니다.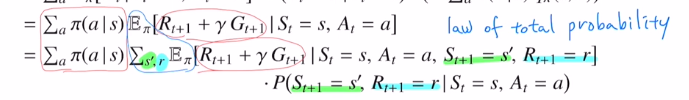
Rt+1=r로 고정되었기에 굳이 확률변수로 적지 않고 r로 적습니다. 이 r은 E밖으로 빠져나옵니다. 현재 조건부에 St=s, St+1=s' 둘 다 있습니다. MDP는 stochastic으로 past는 영향이 없기에 제외시켜도 무방합니다.
그렇기에 이렇게 식을 진행시키기 위해서는 Bellman Equation은 기본적으로 Markov property를 만족할 때 성립이 됩니다.
마지막 부분을 state value ft으로 바꿔줍니다.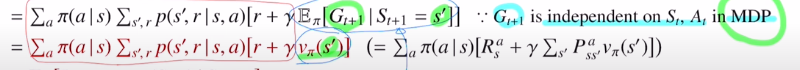
마지막 변형은 각 확률을 곱했기에 , 다시 정리하면 s->a,r,s'이 나올 확률인 것 입니다. 이것이 State-value function에 대한 Bellman expectation Equation입니다.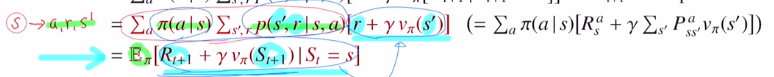
Bellman expectation Equation은 State-value function을 점화식으로 바꿔주는데 immediate reward Rt+1과 discounted next state value γvπ(St+1)의 합으로 분해할 수 있는 것 입니다.
이렇게 했을 때의 장점은 무엇이 있을까요?
이제는 더 이상 return이 필요하지 않습니다! 대신 Rt+1과 St+1만 알면 되는 것 입니다. 이는 에피소드가 전체가 다 끝나지 않아도 계산할 수 있다는 것 입니다!
그렇기에 게임이 끝나지 않아도 중간중간에 state value ft을 계산할 수 있다는 장점이 있습니다. 이것이 Bellman expectation eq를 사용하는 중요한 이유입니다.
다음은 Action-value function를 보겠습니다.
이제는 action이 포함되어 있기 때문에 π(a|s)는 날라가게 됩니다.
아래도 state value ft에서 action만 추가되었습니다.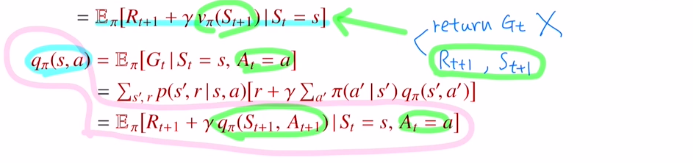
추가적인 내용은 아래와 같습니다.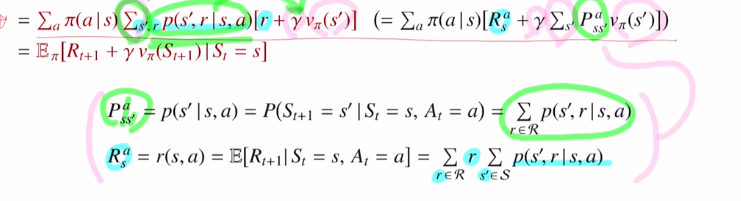
마지막으로 Bellman expectation eq를 backup diagrams로 표현해보겠습니다.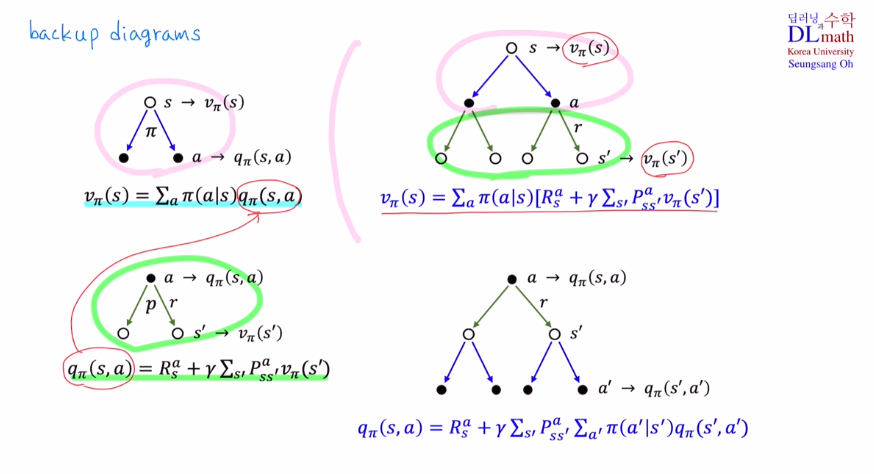
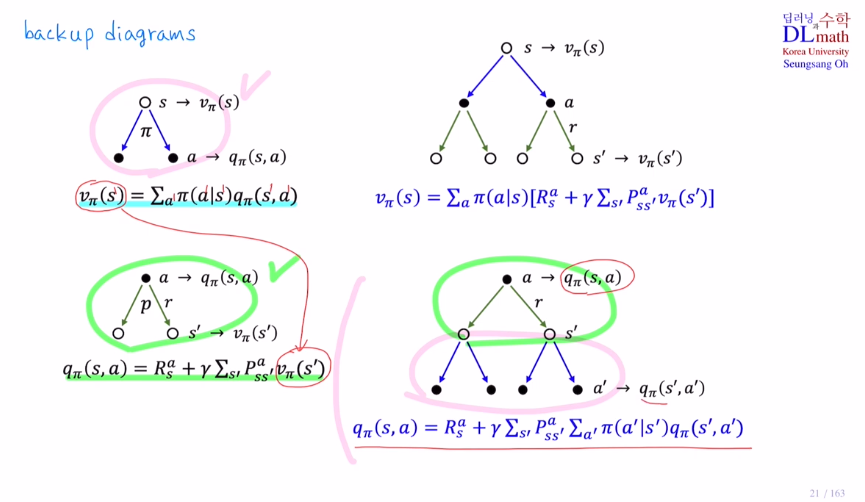
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=Z8RZbcg96Qk&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=5

