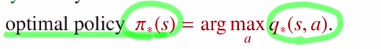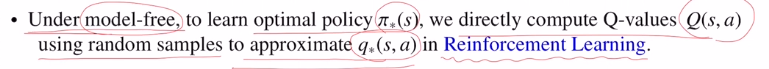이전 포스터에서는 Bellman expectation Equation을 알아보았습니다.
강화학습의 목적은 value ft을 찾는 것이 아닌 reward를 최대화할 수 있는 policy를 찾는 것 입니다. 이를 optimal policy라고 하고, 이것을 찾기 위한 optimal value ft들 optimal state value ft과 optimal action value ft에 대해 알아보겠습니다.
그리고 이것을 찾기 위한 bellman optimality equation에 대해 알아보겠습니다.
먼저 optimal value ft은 최적 가치 함수로 value ft들 중에서 maximum이 되는 것 입니다. 이 optimal value ft들로 optimal policy를 찾게 되고 이를 찾게 되는 것이 Markov Decision process를 해결한 것 입니다.
optimal state value ft
: state s에서 state value ft 값이 maximum이 되는 policy를 적용한 값을 optimal state value ft의 값으로 정의합니다.
optimal action value ft
: 마찬가지로 state action pair에 대해서 action value ft 값이 maximum이 되는 policy를 적용한 값을 optimal action value ft의 값으로 정의합니다.
각 state마다 maximum을 갖는 policy들이 다르게 나올 수도 있습니다.
아래와 같이 각 state마다 이 policy가 많이 다르다면 하나의 policy로 적용하기 어려워집니다.
state value ft값이 높을 수록 앞으로 기대할 수 있는 return 값이 크기 때문에 policy가 더 좋은 것 입니다. 그래서 policy사이에 우선 순위를 주어 ordering을 할 수 있게 해줍니다.
더 좋은 policy : 모든 state에 대해서 state value ft의 값이 더 큰 policy
위와 같은 경우는 π1, π2사이의 order를 비교할 수 없습니다.
optimal policy에 대해 이야기 해 보겠습니다. 말 그대로 최적의 정책인데, 모든 policy보다도 크거나 같은 policy를 말합니다.
이 optimal policy가 존재한다면
state value ft과
action value ft의
모든 state에 대해 하나의 optimal policy로 적용할 수 있는 것 입니다.
여기서 재밌는 점은 MDP에서는
이 optimal policy가 적어도 하나는 항상 존재합니다!
즉, 하나의 optimal policy로 통일할 수 있기에 vπ (s) = v (s)가 되는 것 입니다!
다시 말해, optimal policy를 적용한 state value ft 은 optimal state value ft이 되는 것 입니다.
당연히 action value ft도 마찬가지 입니다.
이것이 MDP의 가장 큰 장점입니다.
이제는 optimal policy를 찾아보겠습니다.
optimal policy를 찾는 방법은
optimal action value ft을 알고 있다면 이것을 maximize하면 됩니다!
식으로 정리하면 아래와 같습니다.
현재 state에서 취할 action a가 optimal action value ft을 최대화 하는 action 이라면 1을 내뱉고 아니면 0을 내뱉습니다. 즉, 최대화 하는 a값 이외의 action은 0을 보내어 100%로 action a만 취하겠다는 것 입니다.(각 q에 대해 항상 최대가 되는 것만 고른다는 것입니다.)
그런데 이 action a가 optimal action value ft값을 최대화하는 것이기에 가장 좋은 action이 되어 이것이 optimal policy가 되는 것 입니다.
모든 state action pair에 대해 optimal action value ft값을 찾을 수 있다고 하면 가장 이상적입니다.
이렇게 되면 각 state에서 어떤 action을 취할지 정해진 것이기에 deterministic policy가 됩니다. 즉, optimal policy는 deterministic optimal policy입니다. 또한 이것이 MDP에서는 적어도 하나가 존재합니다!
추가적으로 식을 정리하면 optimal state value ft과 optimal action value ft을 정리할 수 있습니다. 그렇기에 optimal action value ft을 알면 optimal state value ft을 알 수 있는 것 입니다.
optimal action value ft은 optimal state value ft에서 직접적으로 얻을 수 있지는 않습니다. 왜냐하면 두 번째 식에서는 알기 위해 transition probability를 알아야 하기 때문입니다. 이것을 안다는 말은 model-based일 때, 즉 known MDP일 때 가능한 것 입니다.
optimal policy를 알기 위해 optimal action value ft을 알아야 하고
optimal state value ft을 알려면 optimal action value ft를 알면 알 수 있지만, 그에 반해 optimal policy를 알기 위해 필요한 optimal action value ft을 알기 위해서는 optimal state value ft뿐 아니라 transition probability를 알아야 하기에 애초에 model-based 즉, known MDP일 때 이 연계성으로 optimal policy를 얻을 수 있는 것 입니다!
model-based로 transition probability를 안다 -> 이것과 optimal state value ft을 통해 optimal action value ft을 안다 -> 이것을 통해 optimal policy를 얻는다.
하지만 model-free의 경우는 찾을 수 없기에 반드시 optimal action value ft을 찾아야 optiaml policy를 계산할 수 있게 되는 것 입니다.
따라서 이 경우에는 optimal action value ft을 approximate하는 그런 estimator를 계산하기 위해 강화학습을 이용합니다.
따라서 Dynamic programming의 경우는 optimal state value ft을 찾으려 초점을 두고, RL의 경우는 optimal action value ft을 찾는데 초점을 둡니다.
optimal value ft들을 찾는데 필요한 Bellman optimality equation을 살펴보겠습니다.
optimal state value ft에 대한 Bellman optimality equation
이 식을 증명하는 과정은 지난 포스터에서 알아봤던 optimal expectation equation을 계산하는 과정과 유사합니다.
opitmal state value ft으로 바뀌고 maximize하는 부부만 바뀌었습니다.
여기서 known MDP라면 즉, transition probabiliy와 reward를 알고 있다면 이 공식을 반복적으로 사용하여 optimal state value ft값을 계산할 수 있습니다.
optimal action value ft에 대한 Bellman optimality equation
여기서도 optimal policy로 바뀌고 maximize하는 것으로 바뀌었습니다.
여기서도 known MDP라면 즉, transition probabiliy와 reward를 알고 있다면 이 공식을 반복적으로 사용하여 optimal action value ft값을 계산할 수 있습니다.
이렇게 iterative하게 계산할 수 있는데 이 방법이 Dynamic programming입니다.
optimal state value ft을 찾는 것이 수월하기에 먼저 찾고 진행하게 됩니다.
마지막으로 Bellman optimality equation을 backup 으로 보겠습니다.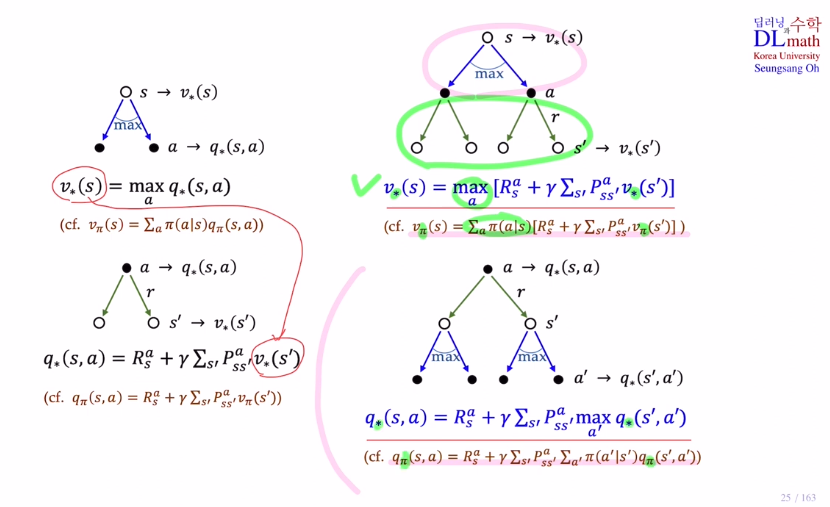
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=WoJoB1D69cA&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=6