이번 포스터는 Dynamic Programming으로 동적계획법에 대해 알아보겠습니다!
복잡한 문제를 여러개의 간단한 문제로 나누어 효율적으로 푸는 방법입니다.
DP는 planning (계획) 으로 <-> learning (학습) 과 상반됩니다.
DP는 복잡한 문제를 작은 문제로 나누어 직접 계산을 하는 것이며, 강화학습의 learning은 그것을 직접 계산할 수 없기 때문에 컴퓨터가 학습하는 것을 말합니다. 이런 면에서 서로 대조적입니다.
DP는 세 가지 핵심 요소로 구성되어 있습니다.
Substructure : original 복잡한 하나의 큰 문제를 간단한 작은 문제 여러개로 나눕니다.
Table Structure : 작은 문제들을 계산한 후에 해답들을 테이블에 기록하는 것 입니다. 이후 이를 반복적으로 사용합니다.
Bottom-up Computation : 밑에 있는 작은 문제들을 풀어 위에 있는 큰 문제를 해결한다는 것 입니다. 테이블에 있는 작은 문제들의 해답을을 사용하여 조금 더 큰 문제에 대한 해답을 구하고 결국 최종 큰 문제에 대한 해답을 얻는 것 입니다.
어떤 문제들이 DP를 사용하는 것이 효율적인지 알아보겠습니다.
1) optimal structure
궁극적으로 풀고 싶은 큰 문제의 optimal solution이 작은 문제들의 optimal solution으로 얻을 수 있다는 것 입니다.
ex) shortest path problem
start - end로 갈 때 가장 짧은 path를 찾는 문제입니다. 이를 작은 문제로 나누어 shortest path를 찾아 연결하여 큰 문제에 대한 답을 정하는 것 입니다.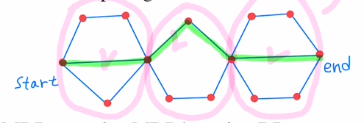
2) overlapping sub-problems
이 성질도 중요합니다. 작은 문제들에 대한 solution이 반복적으로 사용되는 경우(위 shortest 문제의 경우는 작은 문제의 해답이 한 번만 쓰임) 이 해답들을 테이블에 저장해 두고 반복적으로 사용합니다.
많은 문제들을 수학적으로 잘 모델링한 것이 Markoc Decision Process라고 했는데, 이는 위의 두 성질들을 잘 갖고 있습니다.
:Bellman equation을 통해 recursive decomposition으로 잘 나눌 수 있게 하고,
:vlaue ft으로 인해 작은 문제들에 대한 해답을 저장하고 반복적으로 사용합니다.
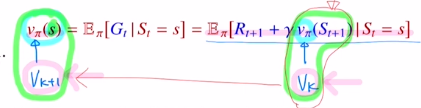
Known MDP는 transition probability, reward를 알고 있는 것이기에 planning으로 다 계산이 가능합니다. 따라서 DP를 통해 MDP를 푸는 것 입니다.
이번에는 Sequential Decision Problem:순차적 행동결정 문제 에 대해 두 가지 solution을 알아보겠습니다. 이것을 수학적으로 정의한 것이 Markov Decision Process이기에 이것으로 이해해도 괜찮습니다.
각 time step마다 action을 구해야 하는 문제입니다.
두 가지 방법은 다이나믹 프로그래밍과 강화학습입니다.
우선 transitoin probability와 reward를 아느냐 모르느냐에 따라 구분됩니다. 알고 있으면 known MDP:model-based, 모르면 unknown MDP:model-free 입니다.
다이나믹 프로그래밍은 모든 state에 대해 계산을 해야 하기에 방대합니다. 그렇기에 DP에서 planning은 value ft들을 계산하는 것 입니다. 방대한 양의 계산을 위해 훨씬 작은 문제들로 분할합니다. 작은 문제들의 답 즉, value ft의 값을 테이블에 저장합니다. 이렇게 차근차근 테이블의 값들을 이용하여 큰 문제의 해답을 구해나갑니다.
하지만 DP의 세 가지 문제가 있습니다.
1) 계산복잡도 : 작은 문제로 나누는데 한계가 있습니다.
2) 차원의 저주 : 테이블에 저장하는데 state space가 너무 커지면 다 기록을 할 수 없게 됩니다. 그렇기에 state space가 어느정도 한정되어 있어야 한다는 점입니다.
3) 환경에 대한 완벽한 정보가 필요 : transition prob 과 reward를 알고 있어야 합니다.
강화학습은 incomplete information을 갖고 있기에 정확한 계산이 불가합니다.
따라서 learning을 합니다. 직접 계산이 아닌 학습을 한다는 것 입니다.
현재 state action -환경-> next state& reward 가 데이터가 되는 것이며,
이러한 데이터가 쌓임으로 이를 통해 학습하는 것 입니다.
이 데이터를 real experience라고 합니다.
계속 얻어지는 reward가 있을 텐데 이 reward의 sum인 total reward를 계산하고 policy를 평가하여 total reward를 maximize하는 방향으로 policy를 update해 나가는 것 입니다. 이것이 강화학습의 기본 틀입니다.
따라서 강화학습은 주어진 데이터에 대해서만 계산을 진행하기에 계산복잡도나 차원의 저주를 해결할 수 있습니다.
앞으로 알아가게 될 모델들입니다.
DP (모든 state value ft값을 알아야 update가능 : full backup)
/ RL : MC(끝까지 간다 : sample multi-step backup), TD (next step까지만 간다 : sample backup)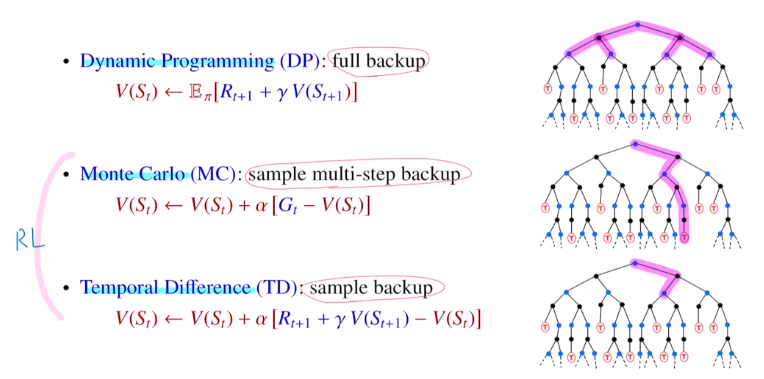
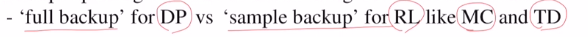
다시 리뷰하면 state value ft을 모든 state에 대한 return의 기댓값을 Bellman eq를 통해 모든 return을 계산하지 않아도 immediate reward와 next state에 대한 state value ft을 가지고 계산을 할 수 있었습니다.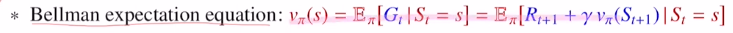
여기서 backup 이 나오는데 위의 벨만 eq를 이용하여 바뀐 식을 통해 update하는 방식입니다. 중요한 것은 현재 state의 state value ft값을 update할 때 future state value ft값을 사용한다는 것 입니다.
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=4i_ycR6uCdQ&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=7
