
Deep Neural network의 학습 능력을 어떻게 평가할 것인가?!
=> Universal Approximation Theorem
중요한 문제
1) 성능이 어디까지가 한계인지 2) 최대한 단순하게 구조를 짜기
아래 그림은 perceptron 다음으로 가장 간단한 hidden layer하나
만약 마지막에 activation ft을 씌우지 않는다면 더 식이 간단해질텐데, 이것만으로도 설명 가능할까?
아무리 원하는 오차를 작게 잡아도 그에 만족하게 학습이 가능하다!
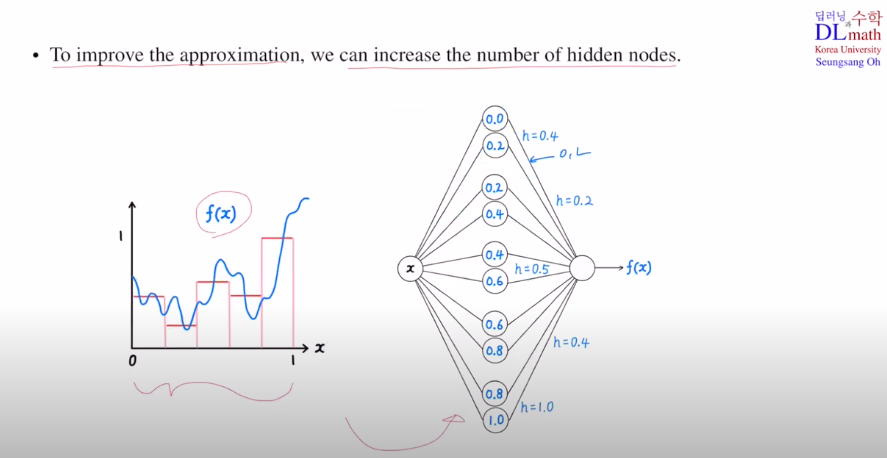
hidden layer의 node수가 많을 수록 성능이 좋아진다.

어떤 input값이 주어지더라도 아주 가깝게 추정할 수 있다.
w와 b에 따라 step ft을 구상할 수 있는데, 아래의 그림과 같이 b/w가 고정되어 있다면 w값이 커질 수록 기울기는 급격해질 것이고, step ft(0.4기준으로 0or1)을 만들 수 있게 된다.
오른쪽 아래를 보면, 0.4를 기준으로 높이는 0.8(두 번째 weight에 의해)이 되고, 0.6을 기준으로 높이는 -0.8이 된다. 이 둘을 sum하면 최종적으로 그림과 같이 bump ft이 생성할 수 있는 것이다!
즉, 원하는 곳에서 bump시킬 수 있다면 f(x)와 같이 복잡한 식을 표현할 수 있게 되는 것이다.
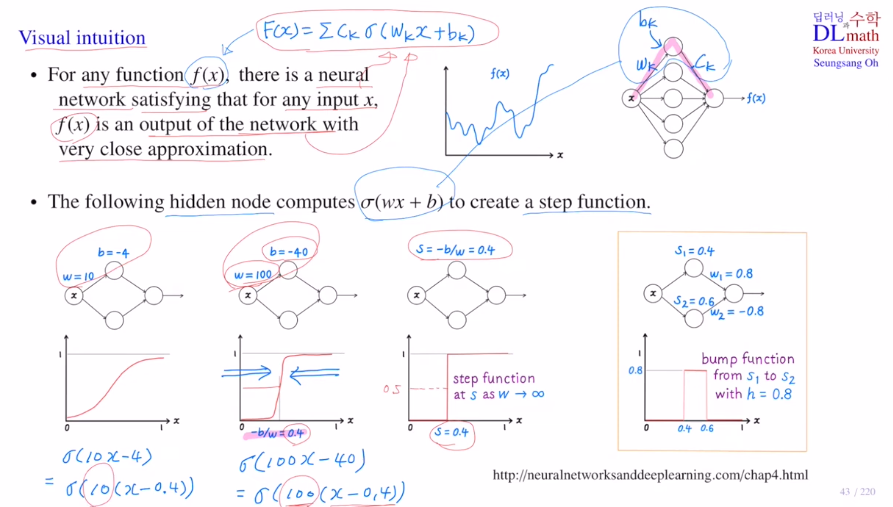
아래와 같이 첫 번째부터 두 번째 노드는 0과 2를 가질 수 있게 w와 b를 조절한다. 나머지 값들도 이와 같이 조정한다.
두 번째 layer를 지날 때, w를 이용하여 높이를 조절하여 f(x)와 유사하게 변형시킨다.
이렇게 점점 bump ft의 개수를 무수히 늘려나가며 높이 또한 조절한다면 f(x)에 굉장히 근사시킬 수 있게 된다! 그렇기에 우리가 원하는 오차 범위 내로 무조건 조절할 수 있는 것이다.
다시 말해, 어떤 함수 f가 주어지더라도 hidden layer 하나만 있어도 우리가 원하는 오차범위 내로 무조건 조절이 가능하다!
여기서는 이전에 언급했던 내용을 다룬다.
노드 수가 비슷하다면!
[ hidden layer를 얕게 쌓고 노드 수 늘리기 vs layer를 깊게 쌓기 ]
파라미터가 많으면 많을 수록 좋은 성능을 보이지만, training 속도 또한 느려진다.
그렇기에 이 또한 중요한 과제이다.
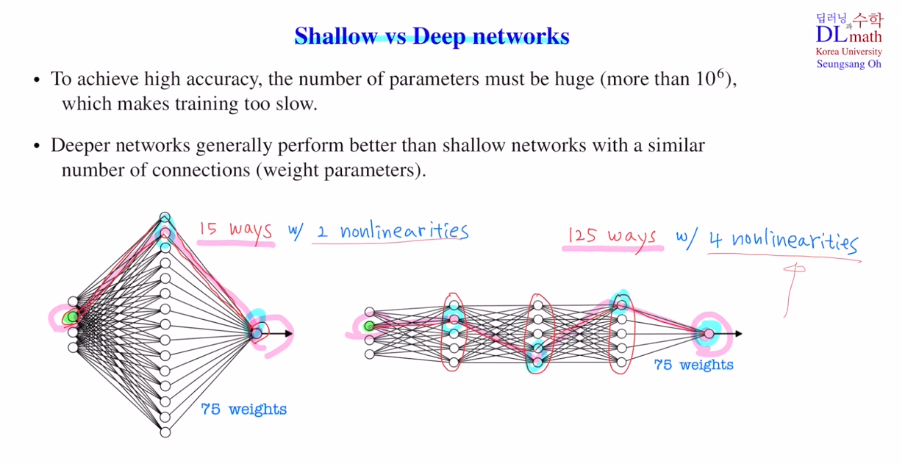
정답을 말하자면 layer를 깊게 쌓을 수록 성능이 좋다!
처음 input layer에서 출발할 때, 최종 output layer에 도달하기 위해 첫 번째 경우는 15가지 방법이 존재한다. 하지만 deep network는 경우의 수가 총 5x5x5로 125가지 방법이 영향을 미치는 것이다. 즉 더욱 다양한 방법으로 영향을 미칠 수 있기에 성능이 우수하며, non-linearity 또한 shallow는 2번, deep은 4번을 거칠 수 있다.
또한 layer가 깊어질 수록 더 고도화된 정교한 특징을 추출할 수 있기에 deep이 더욱 우수한 것이다.
그렇다면 layer를 무조건 깊게만 쌓으면 되는 것인가?
그건 또 아니다. 이전에는 기울기 소실로 인해 깊어질 수록 앞의 weight는 전혀 업데이트가 되지 않기에 성능이 좋지 않은 것이다. 따라서 무작정 깊게 쌓을 수는 없었다.
Hinton교수가 말하는 딥러닝의 한계점 4가지
1) 데이터 숫자 : 이때까지는 지도학습이었기에 딥러닝을 학습시키기 위한 방대한 정답이 있는 데이터의 수가 부족했다. => Big Data, IoT 로 점점 해결되어 가고 있다.
2) 컴퓨팅 파워 : backpropa에서 단순 사칙연산으로 효율적이지만, 이를 병렬적으로 처리하기 위해서는 큰 파워가 필요하다. => GPU, TPU(딥러닝용 하드웨어) 사용
3) 초기값을 그냥 random하게 두었기에 node수가 너무 많아지면 weight sum하고 sigmoid를 취할 때 문제가 생긴다. => 효율적인 weight초기화 방법 : RBM, Xavier, He
4) worng type of nonlinearity 기울기 소실 => ReLU

고려대학교 오승상 교수님 딥러닝 강의 : https://www.youtube.com/watch?v=N6CbPBRR_pw&list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M&index=10
