acitivation ft은 아래와 같이 많은 종류가 있다.
non linearity는 데이터의 복잡한 표현들을 나타내는데 용이하게 해준다.
Q. 왜 활성화 함수를 사용해야 하는가?
활성화함수를 사용하지 않는다면, WL...W1x = Wx로 단순 하나의 layer만 갖는 딥러닝모형이 되는 것이다. 즉, 복잡한 깊은 표현을 할 수 없게 된다.
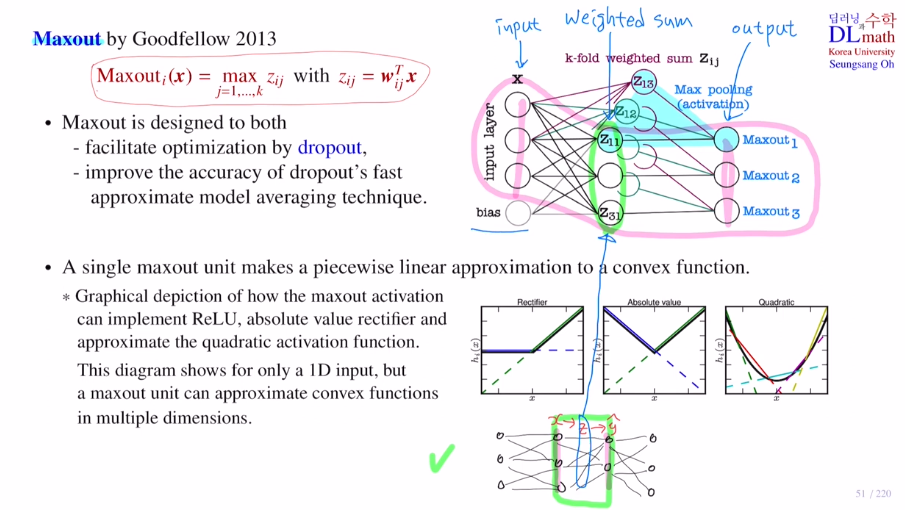
여기서 주의깊게 볼만한 것은 Maxout인데 weighted sum을 한 번하는 것이 아닌 여러번 한다. 이는 relu를 일반화시킨 것으로 이해하면 된다.
그리고 ELU도 relu의 변형인데, diff를 할 수 있게 exponential을 활용한 것이다.

-
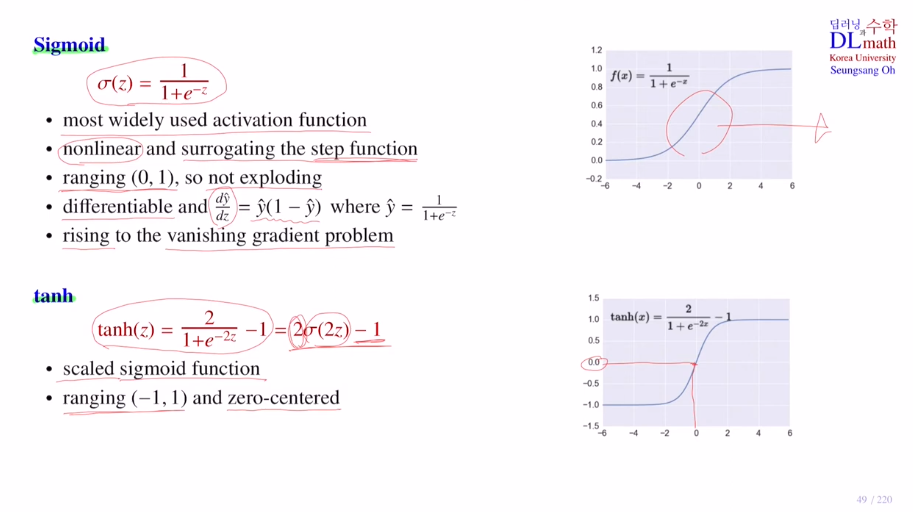
sigmoid
nonlinear이며 step ft의 대용으로 사용된다.
모든 값을 0과1사이로 변경시키기에 exploding이 되지 않는다.
미분 또한 쉽다.
하지만 단점으로 기울기 소실 문제가 있었다. -
tanh
sigmoid의 변형으로 -1에서 1사이의 값을 갖는다. (+zero-centered (0,0))
즉, sigmoid의 스케일링만 다르게 해준 변형이다.
이를 사용하는 이유는 node의 결과값이 0보다 작기도하고 크기도 하기에 사용함, RNN 계열에 주로 사용한다.
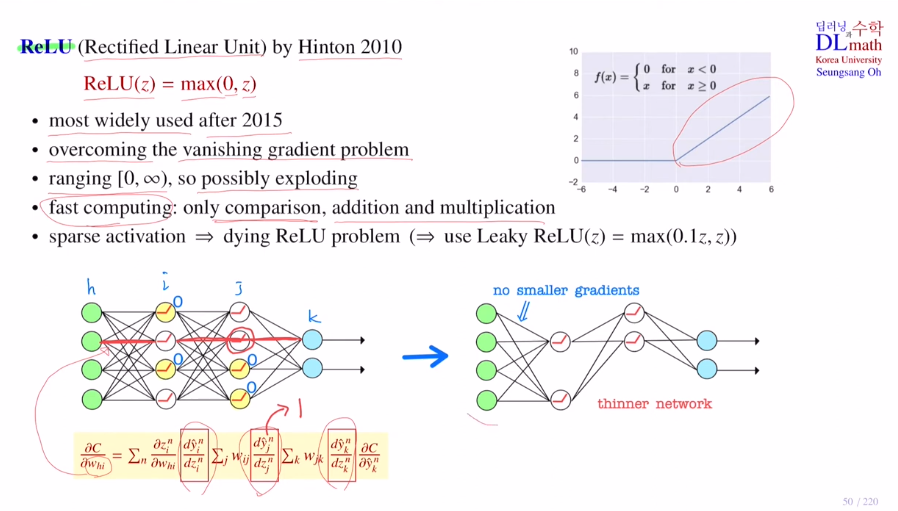
- ReLU(Rectified Linear Unit)
기울기 소실 문제를 해결하고자 고안되었고, 이로 인해 깊은 layer를 쌓을 수 있게 되었다. 0부터 infinite
weigted sum이 음수가 된다면 activation을 거쳐 0값이 된다. 그렇게 되면 그 뒤의 layer로 갈 때 어떤 weight를 갖더라도 0이 나온다. 즉, 아무런 역할을 하지 못 하고 사라지게 되는 것이다! 그 term은 역전파시 0이 곱해져 사라지게 된다. 남은 것들은 미분값이 1이기에 vanishing gradient 문제가 생기지 않는 것이다! thinner network로 sparse activation이라고 한다. 이러한 방식은 차후 나올 dropout 방식과 유사하며 과적합의 문제를 방지하기도 한다! (model averaging효과)차이점이라곤 relu는 input data 정해지는 순간 연쇄적으로 노드가 없어지는 것과 같은 현상이지만, dropout은 미니배치 마다 random으로 노드를 제거하는 것이다.
하지만 weighted sum한 것들이 대부분 음수라면?!
노드가 다 죽어버리게 된다. 이는 dying ReLU problem이라고 하며, 이를 방지하고 나온 것이 Leaky ReLU이다. : max(0.1z, z)
- Maxout
weigted sum한 것이 z일 때, k개 copy를 해둔 것이다. 이 모두를 각 weight를 곱해서 output으로 보내는데, 여기서 Max pooling(activation)을 통해 최대값만을 가져가게 하는 것이다!(이도 dropout과 유사하다.)
학습해야 할 weight는 k개 copy했기에 k배만큼 늘어나게 된다.
사용하는 이유는 dropout과 유사한 성격을 가지기에 최적화를 효율적으로 할 수 있어 사용한다. model averaging효과
relu를 일반화 한 것으로 결국 maximum을 제외한 나머지는 없어지기에 relu와 똑같이 된다.
single maxout unit은 piecewise linear approximation 을 통해 convex ft을 만든다! : 예를 들어 5개 라인을 만들어 각 maximum만 취하면 line segment로 convex ft이 된다.
layer를 깊게 쌓을 수도 있지만 이렇게 만든 Maxout으로 파라미터가 증가하지만 이 활성화함수가 더 효과적일 수도 있다.
고려대학교 오승상 교수님 딥러닝 : https://www.youtube.com/watch?v=DTcSDKSjBv8&t=2s

