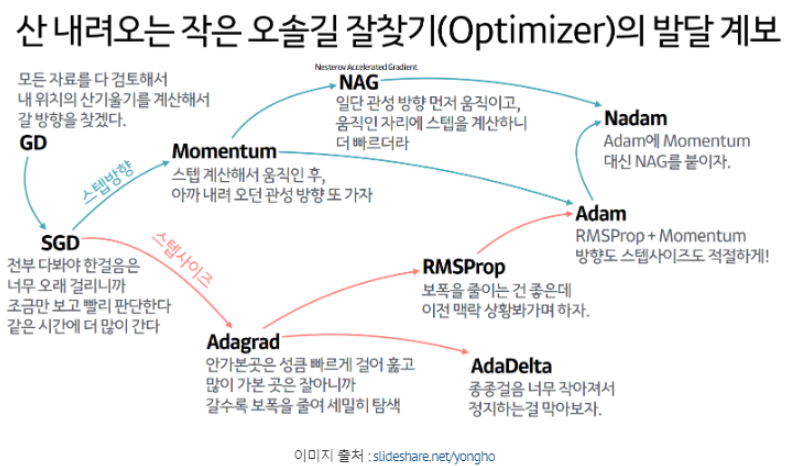
Cost ft의 minimum값으로 다가가야 하는데, 초반에는 크게 움직이고 점점 다가갈 수록 작게 움직이는 것이 가장 효율적일 것이다. : Learning rate decay
이와 관련한 내용들을 알아보자.
VAE 이해하기 위한 내용(1) - Gradient Descent Optimization Algorithms
를 참고하면 수월하게 이해할 수 있을 것이다.
Gradient Descent Optimizers
다양한 방법들이 있는데, SGD는 minibatch GD로 보면 된다.
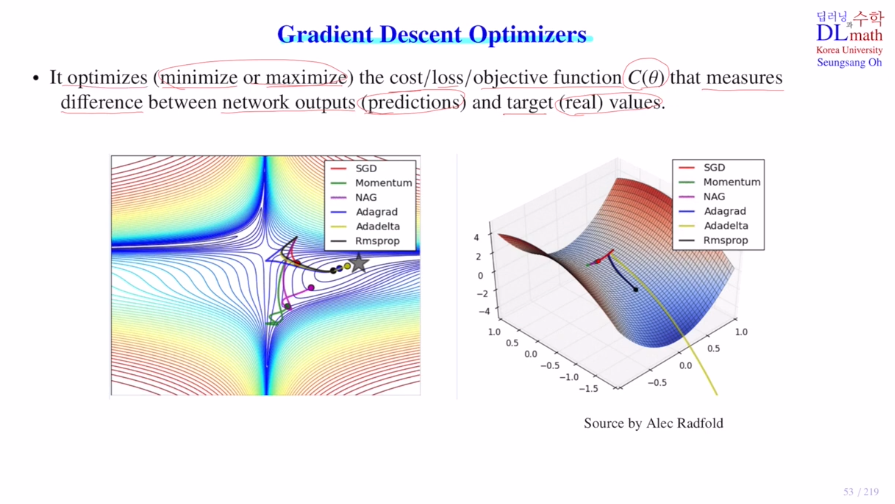
이제 본격적으로 살펴보자!
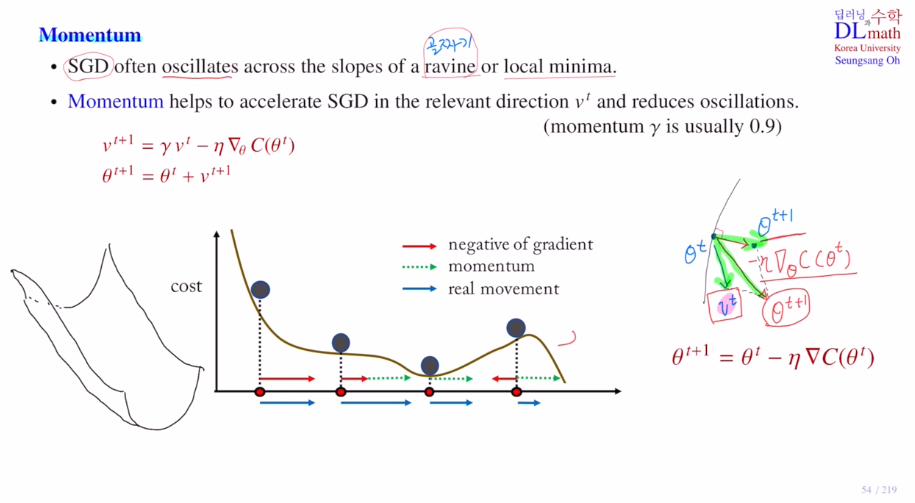
1. Momentum
모멘텀은 이전 SGD에서 일종의 관성을 주는 것이다.
기존의 현재 미분만을 가지고 이동하는 것에 더해서, 과거에 이동했던 방향을 기억하여 그 관성을 가지고 일정 정도를 추가적으로 이동하는 것이다!
여기서 vt가 새롭게 나오게 된다. 감마는 보통 0.9로 하며, 이렇게 구성된 식에 negative gradient를 더해 이동시킨다.
Momentum의 이점!
momentum 방식은 SGD가 Oscilation 현상(반복적으로 변화하는 현상)을 겪을 때 더욱 빛을 발합니다. 기존의 SGD같은 경우에는 최저점으로 이동할 때 step size의 한계로 인해 좌우로 계속 진동하며 이동에 난항을 겪기도 합니다.
하지만 Momentum은 이전의 관성으로 인해 중앙으로 가는 방향에 힘을 얻기 때문에 SGD에 비해 상대적으로 빠르게 이동할 수 있습니다. 또한 local minimum에서 빠져나올 때도 유리합니다. 위와 비슷한 말이지만, 기존의 관성으로 인해 이전 방향성을 가지고 있어 local minimum에서 빠져나와 더욱 좋은 minima로 이동할 수 있습니다.
하지만 momentum 방식을 사용할 때, 기존 변수들 θ 이외에도 과거에 이동했던 양을 변수별로 저장해야하기에 변수에 대한 메모리가 기존의 두 배로 필요하게 됩니다.
γv(t-1)을 쭉 풀어쓴다면 vt는 아래와 같이 표현 가능하며, 'Gradient들의 지수평균을 이용하여 이동한다' 라고 해석할 수 있다.(learning rate를 바꾸지 않는다!)
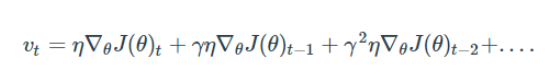
2. Adagrad(Adaptive Gradient)
AdaGrad는 앞과 다르게 learning rate를 조절한다.
Adagrad는 변수들을 업데이트할 때 각각의 변수마다 step size를 다르게 설정하여 이동한다. 기본적인 아이디어는 '지금까지 많이 변화하지 않은 변수들은 step size를 크게 하고, 많이 변화한 변수들은 작게 하자' 이다. 이 아이디어에 대한 근거는 자주 등장하거나 변화를 많이 한 변수들의 경우 optimum에 가까이 있을 확률이 높기에 작은 크기로 이동하면서 세밀한 값을 조정하고, 적게 변화한 변수들은 optimum에 도달하기 위해 많이 이동해야할 확률이 높기 때문이다.
특히 Word2Vec이나 Glov같이 word representation을 학습시킬 경우 단어의 등장 확률에 따라 variable 의 사용 비율이 확연하게 차이나기 때문에 Adagrad와 같은 학습 방식을 이용하면 훨씬 더 좋은 성능을 거둘 수 있다. : good for dealing with sparse data
Adagrad의 한 스텝을 수식화한다면 아래와 같다.
뉴럴 네트워크의 파라미터가 k개라고 할 때, Gt는 k차원 벡터로 써 time step t까지 각 변수가 이동한 gradient의 sum of squares를 저장한다. θ를 업데이트 하는 과정에서 기존 step size η에서 Gt의 루트값에 반비례한 크기로 이동을 진행시키며, 많이 변화한 변수는 적게, 적게 변화한 변수는 많이 이동할 수 있도록 한다. (입실론은 0을 나누는 것을 방지하기 위해 사용합니다)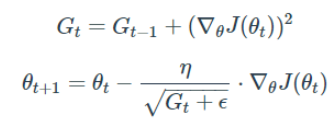
Gt를 업데이트 하는 식에서 제곱은 element-wise 제곱을 의미합니다.
θ를 업데이트 하는 식에서도 ㆍ도 element-wise 곱을 의미합니다.Adagrad를 사용하면 학습을 진행하면서 굳이 step size decay(learning rate) 등을 신경써주지 않아도 알아서 조절해준다는 장점이 있다. (보통 adagrad에서 step size를 0.01 정도로 두고 변경하지 않는다.)
하지만 Adagrad에는 학습을 계속 진행하면 G에 계속 제곱한 값을 넣어주기에 G의 값들은 반복할 수록 증가하고, 이로 인해 step size가 너무 줄어든다는 문제점이 있었다. 이는 결국 step size가 너무 작아져서 움직이지 않게 되어 버린다.
이 단점을 보완한 알고리즘이 RMSProp과 AdaDelta이다.

3. RMSProp
RMSProp은 딥러닝의 대가 제프리 힌톤이 제안한 방법이다. Adagrad의 식에서 gradient의 제곱을 더해나가면서 구한 Gt 부분을 합이 아닌 지수 평균으로 바꾸어 대체한 방법인데, 이는 Adagrad의 단점인 Gt가 무한정으로 커지는 것을 막을 수 있다. 이에 더해 최근 변화량의 변수간 상대적인 크기 차이는 유지할 수 있다.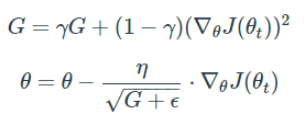
이전 초기 gradient 값에 비해 최근 값이 중요하다. 이를 적용시키기 위한 것으로 여기도 보통 감마 0.9를 사용한다. 이 방법을 사용하면 최근 값을 중요하게 생각할 뿐 아니라, learning rate가 너무 작아지는 것 또한 막을 수 있다.(중요한 테크닉)
4. Adam(Adaptive Moment Estimation)
Adam은 RMSProp과 Momentum 방식을 합친 것과 같은 알고리즘이다. 이 방식에서는 Momentum 방식과 유사하게 지금까지 계산해온 기울기의 지수평균을 저장하며, RMSProp과 유사하게 기울기의 제곱 값의 지수평균을 저장한다.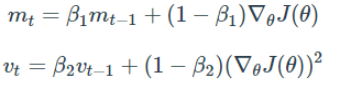
다만 Adam에서는 m과 v가 초기에 0으로 초기화되어 있기에, 학습 초반부에서는 mt, vt가 0에 가깝게 bias 되어있을 것으로 판단하여 이를 unbiased하게 만들어준다.
mt와 vt의 식을 ∑ 형태로 펼친 후에 양변에 expectation을 씌워 정리해보면, 아래와 같은 보정을 통해 unbiased 된 기댓값을 얻을 수 있다. 이 보정된 기댓값들을 가지고 gradient가 들어갈 자리에 mt hat을, Gt가 들어갈 자리에 vt hat을 넣어 계산을 진행한다.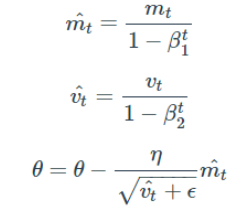
(보통 β1은 0.9, β2는 0.999, ε은 10^(-8) 정도의 값을 사용한다.)

고려대학교 오승상 교수님 딥러닝 : https://www.youtube.com/watch?v=d10dxmyhXmY
