오늘은 Batch Normalization을 알아보자!
이는 Internal Covariate Shift를 방지하고 나온 기법이다.
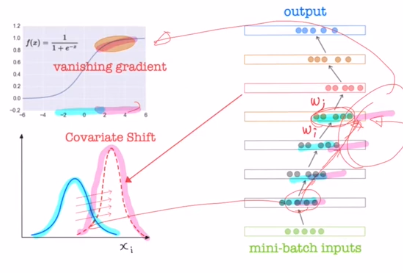
공변량 변화(분포가 바뀌는 것)로 input과 output layer 뿐 아니라 모든 layer에서 발현한다.
weighted sum을 하고 activation ft을 거친 노드에서의 분포는 굉장히 중요하다. 다음 노드로 넘어갈 때 가중치 값을 어떻게 업데이트 시킬지 분포에 따라 바뀌기 때문이다.
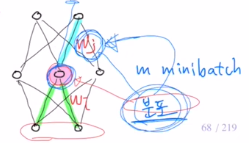
아래와 같은 그림은 mini batch가 5라고 가정했을 때, 각 layer별 노드 하나씩을 표현한 것이다. 이 mini batch의 분포들을 기준으로 각 weight들이 학습하게 된다. 이렇게 업데이트가 되고 다시 iteration을 돌 때, 또 분포가 변화하게 될 것이다. 거듭될 수록 치우치게 된다. 만약 너무 새로운 분포가 들어오면? weight를 학습하는데 어려움을 겪을 것이다.
기존에는 이러한 Internal Covariate Shift를 방지하고자 learning rate를 굉장히 작게 하여 각 layer에 weight가 조금씩 업데이트 되게 하거나 weight initialization을 신중하게 해야 했다.
추가로 이야기 할 문제점이 있다.
[f: saturating <=> z가 무한대로 가도 f(z)가 한정되어 있다.]
sigmoid는 saturating이지만 ReLU는 그렇지 않다.
파란 분포는 위의 sigmoid에서 기울기 소실이 없지만, 만약 거듭되어 분포가 빨간색으로 바뀐다면 기울기 소실 문제가 생기게 되는 것이다. 따라서 saturating non linearity를 사용하는 경우에는 문제가 발생한다.
그렇기에 매 layer 의 각 node 마다 입력값들의 분포를 보정해주는 것이 batch normalization이 나온 것이다. 이전 이야기에서 다루었던 표준화와 정규화는 input data 전체에 대해 조정을 하는 것이었지만, 여기서는 각 iteration마다 각 layer를 거칠 때 입력값의 분포를 매번 조정하는 것이 차이점이다.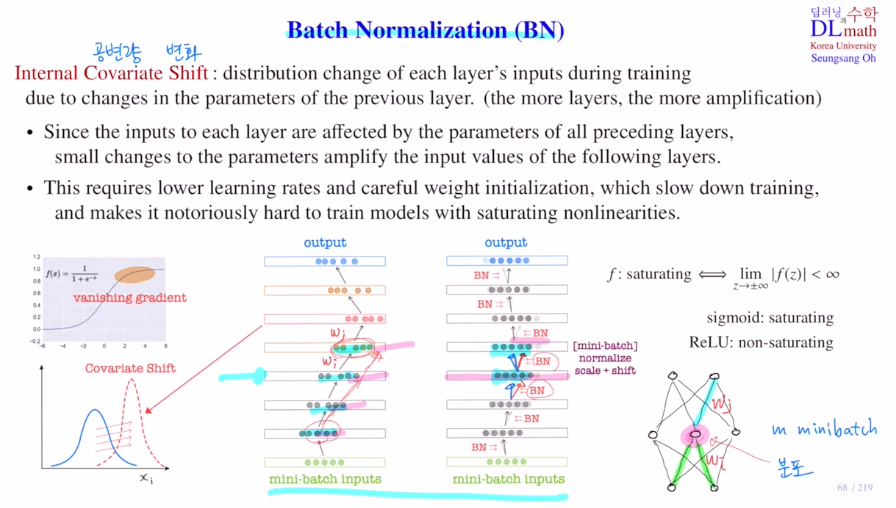
이를 통해 Internal Covariate Shift를 줄일 수 있는 효과를 얻고, learning rate를 줄였던 방법과는 달리 학습 속도를 빠르게 진행시킬 수 있다. 또한 saturating non-linearity를 사용해도 관계가 없고 가중치 초기화에 덜 예민하게 생각해도 된다.
Batch normalization은 각 노드에 독자적으로 적용되는 것이기에, 모두 적용시키는 것이 아니라 특정 노드에만 적용시킬 수 있다. 이를 BN transform이라고 한다.
각 2개의 파라미터가 존재한다. 즉, 100개의 node에 BN을 하려면 200개의 파라미터를 learnable파라미터로 지정해주어야 한다. 하나는 스케일에 관련된, 하나는 shift에 관련된 파라미터이다.
노드값을 a, weighted sum한 것을 x(=Wa+b), 결과값을 yhat이라고 한다면,
yhat = f(Wa+b) => yhat = f(BN(Wa+b)) 가 된다.
Q. 그렇다면 BN이라는 함수는 무엇인가?
k번째 노드에 도착한 weighted sum xi(k)를 xi라고 편의상 표현한다.
이 미니배치 B = {x1,...,xm} (m개 데이터)의 분포를 standardization을 사용하여 바꿔준다. xihat ~ N(0, 1)
하지만 여기서 끝나면 모두 평균 0 편차 1이기에 문제가 생긴다. 따라서 이전 분포에 맞추기 위해 감마만큼 곱해서 scale해주고, 베타만큼 더해서 shift를 하게 된다.
이렇게 분포를 맞춰주어 activation ft을 거치게 되는데, 감마와 베타를 learnable parameter로 잡게 되는 것이다.

test를 진행할 때는 어떻게 할까?
test data를 넣을 때는 미니배치라는 개념이 없기에 조금 변경되어야 한다.
우선 Training부터 살펴보자.
1) 어떤 노드에 BN을 적용할지 정한다.
2) 정한 각 노드들에 BN을 취하여 yhat = f(y) (y=BN(Wa+b))을 만든다.
3) 이제 Cost ft은 기존 파라미터와 감마 베타가 추가된 함수가 된다. SGD를 통해 이 파라미터들을 업데이트 해준다.
이렇게 훈련이 끝난 이후 Test를 살펴보자.
1) 감마와 배타는 미니배치에 의해 학습이 되었기에, 미니배치의 개념이 들어가 있는다.
하지만 test과정에서는 더 이상 미니배치를 사용하지 않는다.
2) 그렇기에 미니배치가 아닌, 전체 데이터에 대해서 평균과 분산을 구한다.
우선 마찬가지로 BN을 적용했던 노드만 고려한다. 하지만! 각 미니배치에서 사용되었던 노드들을 모두 고려한다.
3) E[x] : 지금까지 사용했던 미니배치의 평균들의 평균을 계산(전체 데이터에 대한 값이므로 안전하다)
Var[x] : 분산도 모든 미니배치의 분산의 평균을 계산(m/(m-1) 표본분산을 구할 때 bias를 줄이기 위해 사용하여 unbiased된 것 처럼)
4) 이렇게 만들어진 평균과 분산을 이용해서 test시 하나의 데이터가 들어오면 weighted sum 이후 standard scaling을 하고, 여기에 감마를 곱하고 베타를 더하여 결과를 도출한다.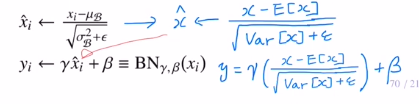
이 BN은 Regularization 역할을 하게 되고, dropout과 같은 역할 또한 해서 때로는 dropout이 필요없을 때가 있다.

추가로 이야기 할 점은 최종 평균과 분산을 구하기 위해 각 iteration마다 각 미니배치들의 평균을 보관하고 있어야 한다. 이를 효율적으로 하고자 moving average를 사용한다.
특정 노드 하나 x를 고정
이 노드로 입력되는 weighted sum이 있을 텐데, 이를 Bt라고 한다.(t번째 iteration에서의 m개 데이터의 weighted sum)
이 Bt의 평균을 뮤Bt, 분산을 시그마Bt^2 이라고 하자.
이랬을 때, E[x]를 moving average로 손쉽게 구할 수 있다. 다 기억할 필요가 없이 이번 미니배치의 평균만을 이용하여 업데이트 시킬 수 있기 때문이다.
이 non-learnable parameter E[x], Var[x]만 정해두어 업데이트하면 되는 것이다.
Tensorflow or keras에서는 모멘텀을 사용하는데, iteration이 지날 수록 1/(T+1) 로 작아지기에 이를 1/100정도로 고정시켜 업데이트를 진행한다. 이렇게 되면 최근의 평균 및 분산 값이 작아지는 것을 막을 뿐 아니라 최근 값을 중요하게 생각할 수 있게 된다.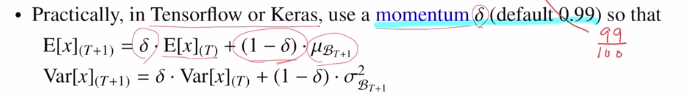
따라서 BN을 사용하게 되면 노드마다 총 4개의 파라미터 (learnable 감마,베타 / non-learnable E,Var) 가 추가된다.
고려대학교 오승상 교수님 딥러닝 강의 : https://www.youtube.com/watch?v=zGvHGlTpevc&list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M&index=17