네트워크의 파라미터들을 초기에는 random으로 할당했다.
하지만 성능이 안 좋았기에 Xavier, He initialization이 등장하며 성능이 개선되었다.
Weight initialization은 Cost가 minimum으로 가게 되는 방향을 수월하게 진행시킬 수 있기에 중요하다. (보통 bias는 영향을 잘 미치지 않기에 0으로 초기화한다고 가정)
1) Zero initialization(or Same Initialization)
모든 weight를 0으로 두는 것이다. 이렇게 되면 weighted sum이 0이 되고 sigmoid를 취하면 모두 0.5가 될 것이다.
모든 weight값이 같다면 역시 동일한 weight sum을 갖고 sigmoid 지나도 역시 동일한 값을 갖는다.
같은 layer의 모든 노드는 같은 값을 갖는다. 그렇기에 gradient값도 같게 나오기에 업데이트 해도 weight의 값들이 같게 나오는 것이다..!
결국 학습해도 하나의 output만 나온다.
2) Random initialization
random하게 weight를 지정해준다.
방법은 두 가지가 있는데 normal distribution N(0, σ^2)과 uniform distribution u[-a, a] 두 가지가 있다.
이 두 분포에서 random sampling하면 평균은 0에 가까운 값이 될 것이다. 하지만 a값을 어떻게 잡느냐에 따라 달라지기도 하기에 0과 떨어진 분포가 될 수도 있다.
만약 N(0, 1)이면 weight값들이 비교적 크게 나올 것이다. 이 가중치 값들로 weight sum을 진행하면 노드 수가 많은 경우 값이 꽤 크게 나올 것이다. 값이 크다? 기울기 소실이 일어난다는 의미이다.
그렇다면 N(0, 0.01^2)로 표준편차를 작게 하면? 가중치가 0에 가까운 값들이 있기에 sigmoid를 지나면 대부분 0.5에 몰려있을 것이다. 뒤layer로 갈 수록 점점 심해지고, 이렇게 되면 노드들이 다양한 값을 가져서 다양한 feature를 가져야 하지만, 그렇지 못 하게 된다.
표준편차를 크게하면 노드의 수가 많을 때 weight sum이 너무 크게 된다. 표준편차를 작게하면 노드의 수가 적을 때 값이 몰리게 된다.
=> 상황에 맞는 적당한 표준편차를 갖고 싶다!
앞의 노드 개수가 적을 때는 weight값을 크게 만들고, 노드가 많을 때는 weight값을 크게 만들자!

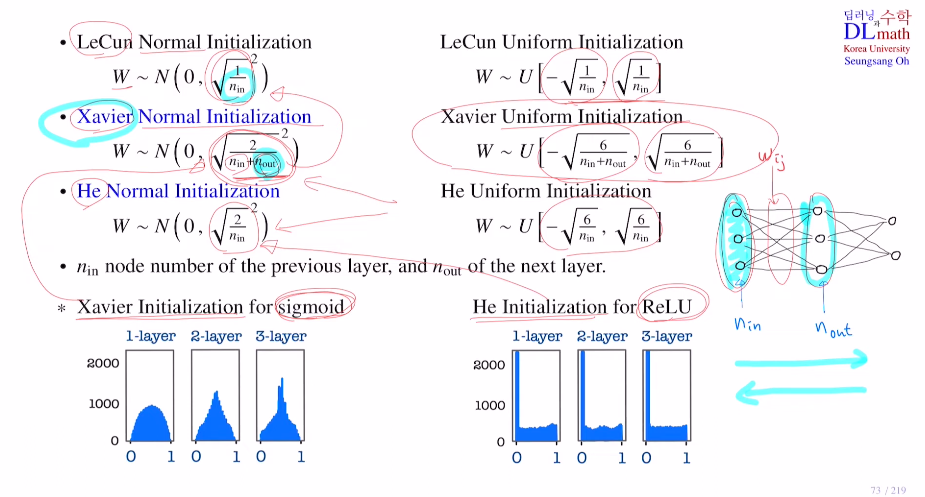
위의 아이디어를 가지고 세 가지 weight initialization 방법을 살펴보자.
1) LeCun Normal Initialization / Uniform Initialization
노드의 개수가 많아질 수록 표준편차 / 구간이 작아진다.
2) Xavier Normal Initialization / Uniform Initialization
자비아는 조금 더 정교하게 바꾸었다.
input node와 output node의 개수 둘 다 이용했다.(둘의 개수가 같으면 LeCun과 똑같다.)
이렇게 한 이유는 forward pass만을 고려한 것이 아니라 추가로 역전파도 고려한 것이다.
3) He Normal Initialization / Uniform Initialization
Xavier와 He는 상황에 따라 쓰인다. activation ft을 sigmoid를 사용한다면 Xavier가, ReLU를 사용한다면 He를 쓰는 것이 유용하다.
그림을 보면 sigmoid를 사용할 때 Xavier를 쓴다면 굉장히 좋은 weight 분포가 나온다. 이로 인해 다양하게 feature들을 만들어낼 수 있다.
ReLU를 사용할 때는 He를 썼을 때, ReLU가 음수는 다 0으로 취하기에 당연히 0에 많이 몰려있다. 0 이외의 부분을 보면 균등하게 잘 퍼져있는 것을 확인할 수 있다.
나머지 시간은 Xavier Normal Initialization을 살펴보자.
h는 activation vector
아래의 그림과 같이 layer가 하나만 있다고 가정하고 진행한다.
Assume
① Linear Regime : activation ft이 tanh처럼 0 근처에서는 f(x)=x로 f'(0)=1인 함수를 사용한다.
② 모든 weight들은 독립변수이고, 등분산성을 갖는다. (초기화시키는 분포를 정하는 것이 목표이기에 모두 같은 분산을 갖는다 가정)
③ 각 layer에 있는 activation vector. 각각의 node값들을 h라 한다. node 값들의 분포도 독립 등분산성
④ weight값들과 activation vector(node값)들은 서로 독립
⑤ weight값들과 activation vector값들의 평균은 0
=> 궁극적인 최종 목표 : 들어가기 전 layer의 각 node의 분포들이 골고루 퍼져있고, 다음 layer의 각 node의 분포들이 골고루 퍼져있게 하자!
다시 말해,
1) forward : Var[hl] = Var[h(l+1)]
2) backward : gradient값들의 분포가 동일하게 하자
=> 이 두 가지를 만족하는 weight를 찾아서 initialization을 시키자!

1) forward : Var[hl] = Var[h(l+1)] 만족하게 하고 싶다.
Var를 씌우면 X,Y독립일 때, Var(X+Y) = Var(X)+Var(Y)이므로, 다 분해가 되고 등분산성을 갖기에 모두 같은 분산으로 가져서 nVar[wh]가 된다. 또 w,h는 독립이기에 분해가 가능하고 둘 다 평균이 0으므로 아래와 같이 나온다.
여기서 Var[hl] = Var[h(l+1)]를 만족시키고 싶기에 이를 만족하기 위해서는 nVar[w]=1인 것이다!
2) backward
activation ft을 tanh처럼 두었기에, 미분해서 0 넣으면 1.
(-> 왜 0을 넣는가? weighted sum값은 평균적으로 0이라 생각할 수 있기에)
따라서 결론적으로 n(l+1)Var[w]=1의 결론을 내게 된다.
이 두 식을 어느정도 충족시키기 위해 일단 더해준다. 이를 정리하면 표준편차 값이 어떻게 나오는지 확인할 수 있다.
(LeCun은 backward를 고려하지 않는다면 그냥 Var[w]=1/n 이기에 백워드를 고려하지 않은 weight분포라고 생각할 수 있다.)

Uniform Initialization을 확인해 보자.
Var[x] = 1/3 * b^2 이 나오는데, 위의 Var[w]=2/(nin+nout) 을 대입하면 도출해낼 수 있다!

고려대학교 오승상 교수님 딥러닝 강의 : https://www.youtube.com/watch?v=oux6MZtPWF8&list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M&index=18

