이전 포스트의 내용을 리뷰하자면 에를 들어 단어 xi들을 word embedding(dim=100)을 통해 변경했다고 가정하자. 이들은 각 layer마다 들어오게 될텐데, layer이 노드수가 50이라고 하면 5000개의 파라미터가 필요하게 된다. 시퀀스의 길이가 1000이 된다면 오백만개의 weight를 학습해야 하는 것이다. 하지만 우리의 목표는 적은 computation, 적은 # weights이기에 weight sharing을 통해 BPTT로 진행하는 방법을 사용하였다.
이 상황에서 만약 data의 수가 너무 많다면?!
이런 경우는 중간부터 보아도 괜찮은 경우가 많기에 오늘 알아 볼 truncated BPTT를 사용하게 된다.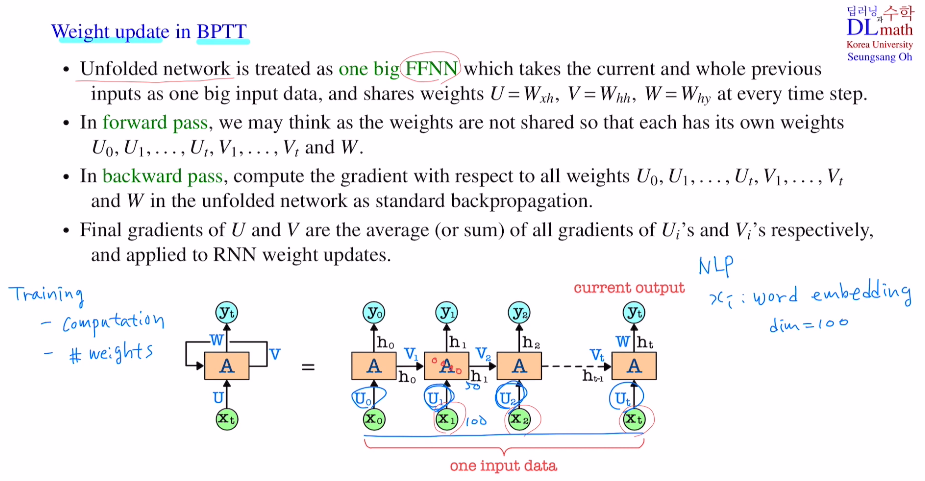
학습해야 할 data가 너무 많은 경우 계산량이 너무 많아지는 문제와 gradient를 축적시키는 과정에서 앞 쪽에 있는 weight gradient를 계산할 때 wij는 모두 같은 것이기에 같은 값이 계속해서 곱해져 gradient값이 너무 커지거나 작아지는 문제가 있다.(Wij가 1보다 크면 너무 커지고, 1보다 작은면 0에 수렴하고)
이 두 문제를 막기 위해 적당히 끊어주는 것이다.
backpropagatoin을 진행할 때 time step의 수를 제한한다.(하이퍼 파리미터)
전체를 사용하지 않았기에 일종의 estimation이 된다.
input sequence를 잘라 subsequence를 만든다. 5라고 잡았으면 각각이 subsequence가 된다.(주식 같은 경우는 꽤 길게 잡는다.)
중요한 점은 이를 중첩시켜서 overlapping이 되게 만든다는 점이다. 이 하나를 trainig sample로 생각한다.
RNN의 input data는 3D tensor로 (batch size, timestep, input dim)이 된다.
예를 들어 1 iteration에서 weight update를 할 때, batch size=100, timestep=5로 했다면 100개의 5개 xi로 구성된 subsequence들을 가져와 이를 통해 weight update를 하는 것이다.
아래의 그림과 같이 5개 data로 이루어진 subsequence로 gradient의 평균 및 합을 구해두고, mini batch size인 5개의 subsequence로 각각 구해두었던 gradient 평균들의 평균 및 합으로 weight update를 진행하고 이를 반복하는 것이다!
참고할 부분은 subsequence 내의 데이터는 시간적 정보가 있어 섞으면 안 되지만, 미니배치 내의 각 subsequence들은 서로 shuffle을 해도 상관없다.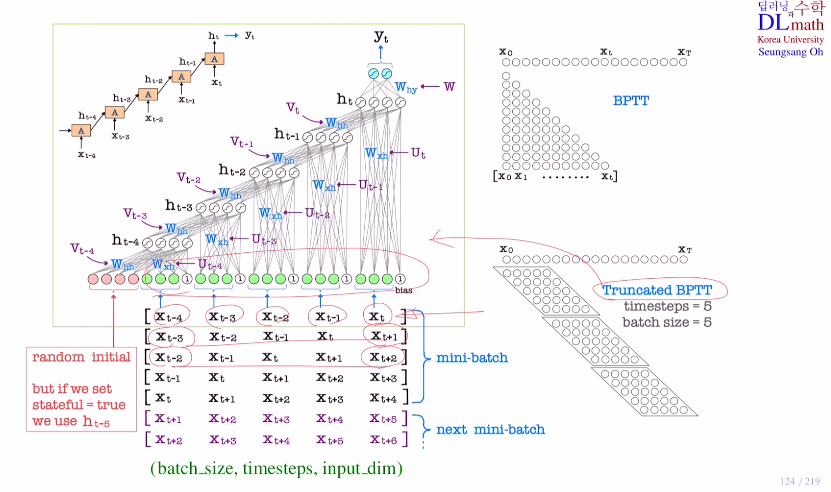
또한 처음 input data는 어떤 hidden state와 결합할까?
이는 random innitial로 가져올 수도 있지만, stateful=True로 설정한다면 이전의 ht-5를 가져와서 참고할 수 있기에 효율적으로 사용하게 된다.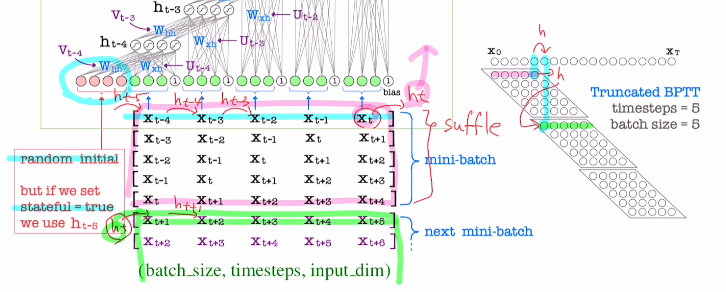
이렇게 사용할 때는 아래와 같이 사용하지 않도록 주의해야 한다.
그렇기에 stateful=True로 설정할 땐 미니배치 내의 subsequence간 shuffle을 진행하면 안 된다!!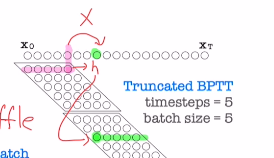
이를 State maintenance라고 한다.
Default mode
미니배치 내의 subsequence들은 독립이기에 shuffle을 해도 아무 상관이 없다.
(xt를 계산할 땐 xt-4 ~ xt-1의 정보만 사용하기에)
Statefule mode
하지만 stateful=True 로 사용한다면 이번에 사용했던 ht를 다음 미니배치의 첫 번째 샘플에 사용해야 하기에 shuffle을 진행하면 안 된다! 이전의 함축된 정보들을 사용할 수 있어 random initial보다는 효율적이다.
또한 stateful mode를 진행할 때는 미니 배치 내의 데이터 개수는 동일해야 한다.
고려대학교 오승상 교수님 딥러닝 강의 : https://www.youtube.com/watch?v=NfHyWq6bYgA&list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M&index=29
