Auto-Encoder는 AE라고 불리며 AE의 세 가지 특징이 있다.
우선 unsupervised learning이고, data reconstruction 구조를 갖고 마지막으로 encoding-decoding구조를 가진다는 것이다.
AE는 비지도학습으로 label이 없어도 학습이 가능하다. 그렇기에 활용도가 아주 높다.
기존에는 output을 생성하고 기존의 target과 비교하여 오차를 구했는데, AE에서는 이 target을 input을 가져와 사용한다. 이를 통해 output이 input처럼 되게 재구성하는 것이다. 이를 data reconstruction라고 한다. 아래를 보면 conv 를 통해 input을 Latent vector로 바꾼다. 이를 디코더를 통해 transposed conv로 up sampling을 통해 다시 input과 유사한 그림을 만드는 것이다. 이 output을 reconstruction output이라고 하며 input이 target이 되는 것이다. 그렇기에 따로 label이 없으므로 비지도 학습이다.
세 가지 특징으로 Dimensionality reduction, Data-specific, Lossy가 있다.
인코더에서 latent vector를 만들고, 디코더에서 이를 통해 output을 만든다. 이렇게 정보 손실을 줄이며 만드는 것이 Auto Encoder이다.
의미 있게 압축을 위해 input data feature들의 correlation이 높아야 한다.(고양이만 많이 모은 것) 또한 test에서 training과 비슷한 이미지를 넣어야당 성능이 좋다.
마지막 Lossy는 input을 줄여 latent vector를 만들고 다시 복원시킨 것이기에 당연히 input에 비해서는 정보 손실로 인해 output이 흐리고 안 좋다.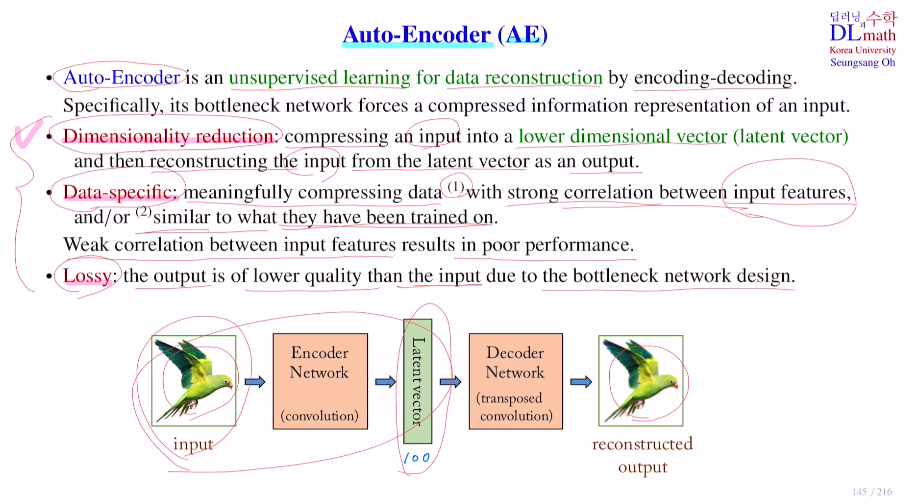
MNIST를 통해 예시를 보자.
우리의 목적은 input을 인코더를 통해 latent vector로 만들고 디코더로 다시 복원시키고. 이 이미지를 input과 비교하여 loss를 구해 latent vector가 최대한 잘 함축할 수 있게 하고 output을 target과 최대한 유사하게 만드는 것이 목표이다.
Loss ft은 픽셀들의 값의 차이를 MSE를 사용하며, 데이터가 0과1만 있다면 binary cross entropy를 사용한다. 기본적으로 FFNN을 사용하기에 표준 역전파를 사용하면 된다.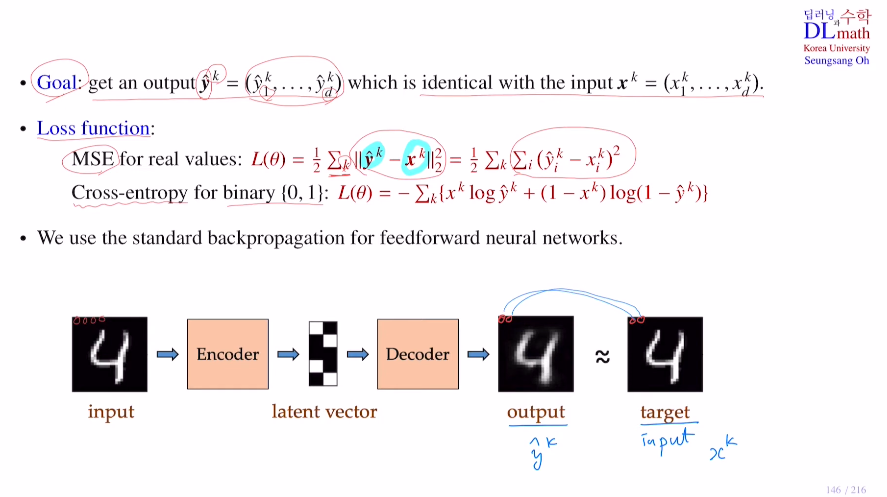
Dimensionality reduction
AE의 두 가지 응용이 있는데, 첫 번째는 Auto-Encoder를 통해 기존 input을 줄여서 이를 다른 알고리즘에(classification, clustering, anomaly detection(이상탐지) 등) lower dim input으로 사용 가능하다. 두 번째는 기존의 데이터의 dim이 큰 경우 visualizaiton이 불가능할 때가 있는데, 데이터를 작게 하여 2D, 3D로 visualization이 가능하게 한다.
AE를 통해 이미지를 dim=5짜리 latent vector로 바꾸려고 한다.(중요하다고 생각하는 5가지 feature(attribute) 값을 찾아 사람의 information을 대신한다.)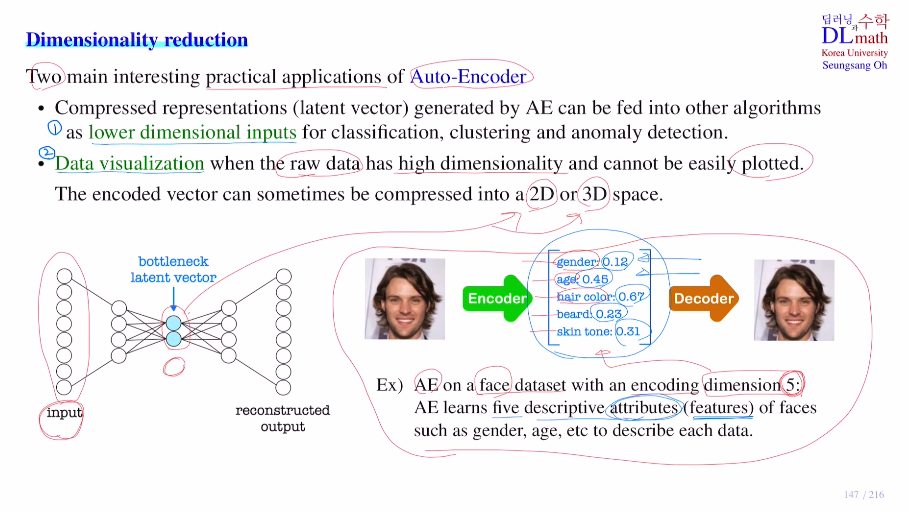
대표적으로 Dimensionality reduction을 하는 두 가지 이유가 있다.
첫 번째는 딥러닝을 사용하지 않은 PCA 주성분분석 이다.
두 번째는 Auto-Encoder이다.
예를 들어 아래의 2D 점들이 있을 때 이를 1D로 표현하고자 하면 어떻게 할 수 있을까?
가장 쉬운 방법은 PCA로 linear 빨간 선(이를 Hyperplane이라고 한다.)에 projection을 시키는 것이다. 하지만 선을 기준으로 반대편에 있지만 정사영시키면 가까워져버리는 경우가 생긴다. 그렇다면 곡선(non linear : mainfold)으로 표현한 후 이를 펼쳐보자. 이는 방법은 조금 더 용이하며 이것을 Auto-Encoder를 쓰는 방법이다.(weighted sum은 linear지만 non-linearity가 추가되기에 nonlinear mainfold를 사용한 것이다. PCA의 일반화 버젼이라고 생각하면 된다.)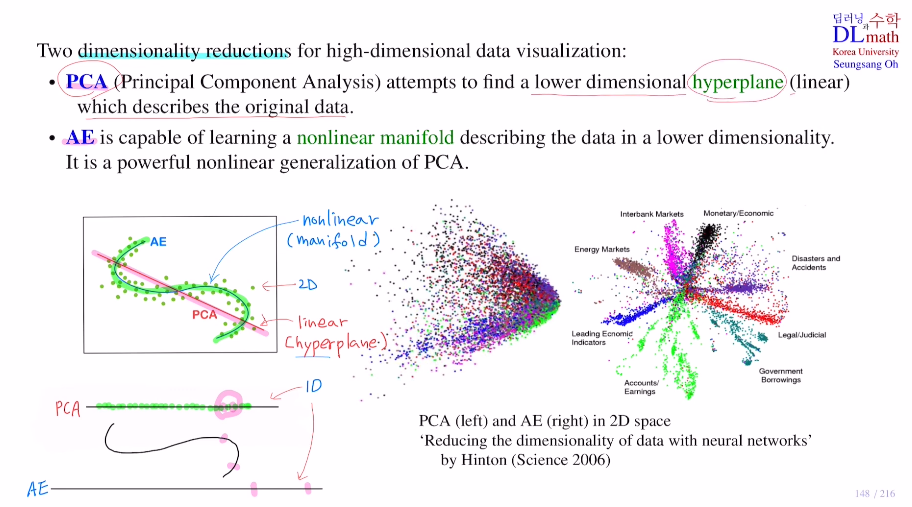
만약 3차원 공간에 각 데이터 셋이 아래와 같이 꽃봉우리 처럼 있을 때, 이를 2D로 바꾼다고 하자. PCA는 평면에 그대로 projection하기에 그림의 왼쪽과 같이 잘 구분하지 못 한다. 그에 반해 AE는 아래와 같은 곡면으로 보낸 뒤 펼쳐서 2D로 바꾸기에 오른쪽과 같이 데이터 셋을 서로 잘 분리할 수 있게 된다. 따라서 새로운 데이터가 들어왔을 때도 어느 클래스에 들어가는 지 잘 구분할 수 있다.
(PCA는 딥러닝이 아니기에 적은 데이터만으로도 수학적 방법을 통해 구할 수 있지만, AE는 딥러닝 기법이기에 데이터가 충분하지 않다면 애초에 학습이 불가능하다는 차이는 있다. 하지만 일반적으로는 AE가 훨씬 용이하다.)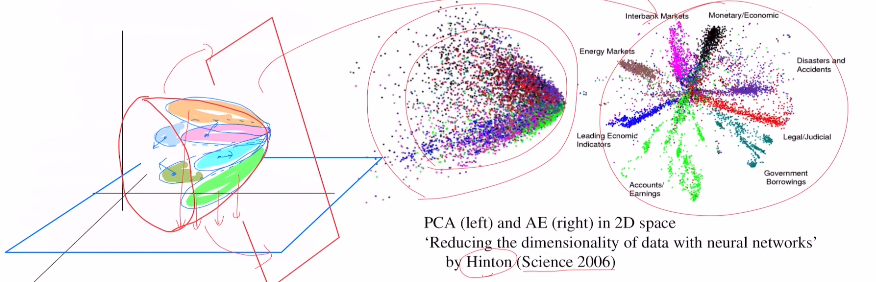
고려대학교 오승상 교수님 딥러닝 : https://www.youtube.com/watch?v=1QcttO3rKmw&list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M&index=34
