이번 포스터에서는 Variational Auto-Encoder : VAE를 알아보자!
VAE : Auto-Encoding Variational Bayes - 논문 리뷰
를 참고하면 좋을 것 같다.
우선 AE의 목적은 output을 만들어 내는 것이 아니라, output을 만들어내게 학습하며 만들어진 즉, input을 low dimension으로 압축을 한 compressed latent vector를 만드는 dimensionality reduction이 목적이다.
하지만 이번에 알아볼 VAE는 사용 목적이 전혀 다르다.
가장 큰 차이점은 안의 VAE는 두 개의 latent vector를 만들어낸다.
하나는 평균에 관한 것, 하나는 표준편차에 관한 것이다.
궁극적으로는 이 평균과 표준편차에 관한 latent vectors로 Gaussian distribution을 표현하고자 한다. N(평균, 분산)
각 attribute마다 가우시안 분포 하나씩을 만들어 내는 것이다.
Q. 그렇다면 왜 두 개의 latent vector를 만들까?
각 attribute마다 posterior distribution p(z|x)을 만들고자 한다.
posterior distribution을 만드는 것은 거의 불가능에 가깝다. input x에 대해 만들어진 input을 잘 표현하기 위한 attribute z값들은 분포가 상당히 복잡할 수 밖에 없다. 이를 찾는다는 것은 불가능하다. 따라서 p(z|x)에 대해 가우시안 분포를 통해 approximation을 취한다. 즉, 평균과 표준편차만을 찾으면 되는 것이다. 이 평균과 표준편차를 VAE의 인코더 파트에서 찾아내는 것이다.
이런식으로 posterior distribution이 복잡하기 때문에 다루기 쉬운 가우시안 분포 등을 이용해 approximation을 통해 구하는 것을 variational inference라고 한다.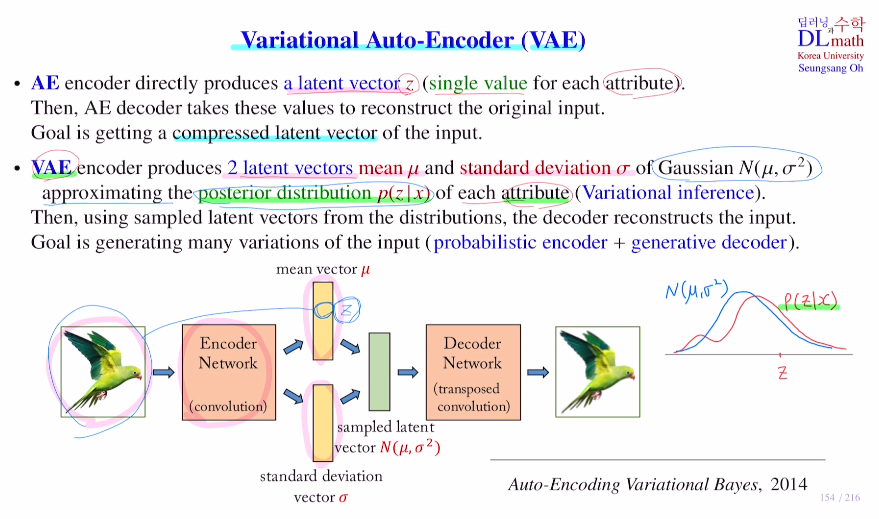
또 다른 궁금증이 있다.
Q. 왜 latent space를 vector로 하지 않고, 굳이 distribution으로 하여 복잡하게 할까?
가장 큰 이유는 distribution으로 함으로써 샘플링이 가능하게 된다는 점이다. 즉, 이 분포를 잘 따르는 sampled latent vector 여러개를 만들 수 있다는 것이다!
이를 통해 기존의 하나의 input에서 하나의 output이 아니라, 각 여러 sampled latent vector들을 통해 디코더파트로 output을 여러가지를 만들 수 있게 된다.
ex) 아래와 같이 하나의 input image로 100개의 sampled latent vector를 만들어 디코더를 통해 input과 비슷하지만 다른 100개의 output을 만들 수 있다!
따라서 VAE를 generate model이라고 한다. 새로운 데이터를 생성하고 싶을 때 이 방법을 사용한다.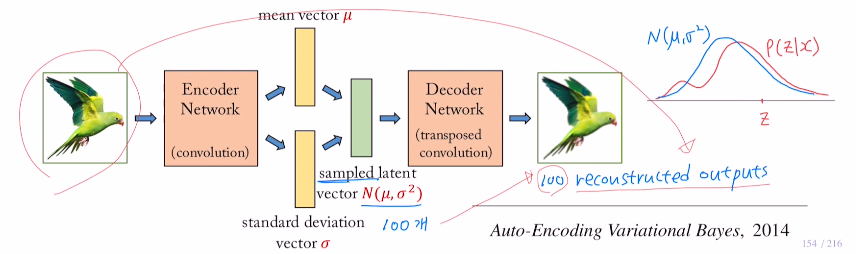
이미지 generate 방법
1) input data를 augementation으로 변화, 픽셀 값들을 바꾸기
이것은 이미지를 크게 변형시키는 것이 아니기에 좋은 방법은 아니다.
2) latent vector를 약간 변화시키기
1의 픽셀을 변경하는 것과 달리 latent vector의 값을 변화시키는 것은 feature를 변화시키는 것이다. 예를 들어 skin tone의 값을 변경하는 등
이것은 의미 있는 데이터가 된다. 하지만 이렇게 변경할 때 어느정도까지 값을 바꿔도 되는 것인가?는 값을 조금만 바꿔도 이상한 그림이 나올 수 있기에 상당히 어려운 문제가 된다. 이를 regularity라고 한다. 이 부분은 다음 포스터에서 다루겠다.
3) 이 부분을 보완하기 위해 나온 것이 VAE이며, 설명했던 바와 같이 분포를 만들어 sampling을 통해 각기 다른 비슷한 image를 generate하는 것이다.
이제 VAE의 인코더 부분을 확인해 보자.
여기서의 목적은 posterior distribution p(z|x)를 만들어 내는 것이다.
하지만 이 분포는 상당히 복잡한데 이를 intractable이라고 한다.
이를 근사하기 위해 정규분포를 통해 approximation을 진행한다.
이 정규분포를 인코더 variational posterior qΘ(z|x)를 통해 approximate한다.
즉, 이를 위해 평균과 표준편차를 찾아내야 한다. 인코더 network qΘ에서 평균과 표준편차를 꺼내기 위한 두 개의 latent vector를 만드는 것이다.
아래의 VAE를 보면 input x에 대해 probabilistic encoder qΘ를 통해 latent vector 두 개를 만든다. 이 평균과 표준편차로 feature에 따른 정규분포들을 만들어 posterior distribution을 approximate한다. 그리고 이 각 feature에 따른 정규분포들에서 각각 샘플링을 하고, 디코더를 통해 비슷하지만 다양한 이미지를 generate하는 것이다!
여기서 추가로 언급할 점은 input x에 대해 인코더 variational posterior qΘ(z|x)를 통해 정규분포를 위한 평균과 표준편차를 만든다고 했는데, 평균과 표준편차를 계산하는 것이 아니라 네트워크가 평균과 표준편차를 나타내는 값을 만들어 내는 것이다! 그렇기에 따로 데이터에 따른 평균과 표준편차를 계산하는 내용은 없다.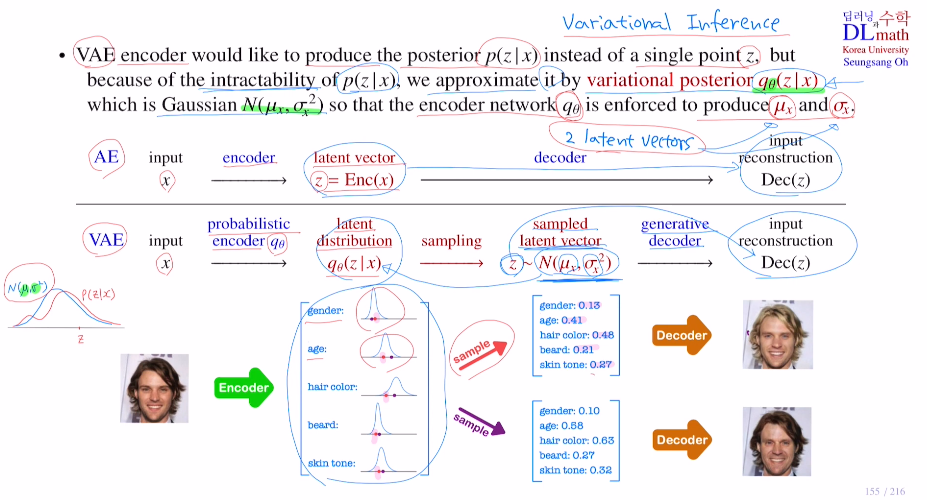
이제는 이 network의 loss ft이 무엇인지 확인해보자.
만약 input을 target으로 잡으면 우선 정규분포에서 샘플로 하나를 얻을 텐데 디코더로 보내 input과 최대한 유사하게 output을 만들 것이다. 그렇게 되면 기존 input과 유사하게 만들기 위해 학습하기에 결국 평균은 AE처럼 z가 되어버리고 표준편차는 0이 되어 버릴 것이다.
이렇게 되면 우리의 목적인 여러 샘플링을 통해 다양한 output을 만들 수 없게 된다.
그렇기에 우리의 목적을 실행하기 위한 Goal은 아래와 같다.
1) 우선적으로 중요한 latent vector로 잘 함축하기 위한 최종 output과 ipnut x의 차이인 reconstruction error 를 줄이는 방향을 학습해야 한다. : 기존 AE의 loss ft인 reconstruction term
2) 이 조건이 추가되는 것인데 표준편차가 0으로 가는 것을 막기 위해 학습하는 latent distribution을 정규분포로 한다고 했는데, 이 분포를 평균은 0이고, 표준편차는 1인 표준정규분포로 만들기 위해 학습을 진행시킨다. : Regularization term이라고 하며 latent space가 regularity를 만족하게 된다.
이 목적을 위해 loss ft은 아래 식과 같이 1을 minimize하고 2와 같이 표준정규분포로 만드는 term이 합해진다. 기존 loss가 있고 오버피팅을 막기 위해 추가로 텀을 더하는 것을 regularization이라고 했기에 이 텀을 regularization term이라고 한다.
(표준정규분포에 근사시키기 위해 KL-divergence를 사용한다. 이는 두 확률 분포 사이의 차이를 나타내는 함수이다.)
(베타는 하이퍼파라미터로 어느 부분에 더 중요시할지 정한다.)
이제 이 loss ft을 통해 각각의 weight parameter를 역전파를 통해 update하고 싶다.
하지만 문제가 생긴다. 바로 output인 yhat을 계산할 때, differentiable ft들로만 계산했지만 여기서는 random sampling과정이 포함되어 있다. 이렇게 random sampling하는 것은 differentiable ft이 아니기 때문에 gradient를 계산할 수 없다. 그렇기에 역전파를 구현할 수 없는 것이다.
따라서 VAE에서는 Reparameterization trick을 사용한다.
가장 핵심적인 내용으로 원칙적으로는 표준정규분포에 근사시킨 N(μ,σ^2)에서 sampling을 실행해야 하지만, 여기서 직접하지 않고 우선 표준정규분포에서 sampling을 하고 sampled latent vector를 z = μ + σㆍε로 만든다. (ㆍ:element wise multiplication)
(ε은 평균이 0이고 표준편차가 1인 정규분포에서 뽑은 것, σㆍε은 평균이 0이고 표준편차가 σ인 정규분포에서 뽑은 것, μ + σㆍε는 평균이 μ이고 표준편차가 σ인 정규분포에서 뽑은 것)
이렇게 되면 N(μ,σ^2)에서 sampling한 것과 동일하게 된다!
이런 Reparameterization trick을 사용함으로 미분이 가능하게 되어 backpropagation을 실행할 수 있게 된다!
고려대학교 오승상 교수님 딥러닝 강의 : https://www.youtube.com/watch?v=yfxytn0OAAg&list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M&index=36
